预约演示
更新于:2025-12-09

Zayed University / Abu Dhabi
更新于:2025-12-09
概览
关联
100 项与 Zayed University / Abu Dhabi 相关的临床结果
登录后查看更多信息
0 项与 Zayed University / Abu Dhabi 相关的专利(医药)
登录后查看更多信息
202
项与 Zayed University / Abu Dhabi 相关的文献(医药)2025-12-31·Medical Education Online
Integrating digital and narrative medicine in modern healthcare: a systematic review
Review
作者: Efthymiou, Efthymia
BACKGROUND:
The increasing integration of digital technologies in healthcare, such as electronic health records, telemedicine, and diagnostic algorithms, has improved efficiency but raised concerns about the depersonalization of care. Narrative medicine has emerged as a pedagogical and clinical response to this shift, emphasizing the value of patient stories, socio-cultural contexts, and reflective practice.
OBJECTIVE:
To understand how digital tools can support, rather than undermine, narrative competencies and contribute to a more human-centered healthcare education.
METHODS:
This review systematically examined empirical and theoretical studies on the integration of digital technologies and narrative medicine within healthcare education. Databases including PubMed, MEDLINE, and Google Scholar were searched using defined inclusion and exclusion criteria. Identified studies were screened, reviewed, and thematically analyzed to extract patterns in outcomes, pedagogical applications, and integration strategies.
RESULTS:
The findings indicate that narrative medicine nurtures empathy, communication, and professional identity formation among healthcare trainees. Digital tools, including virtual reality simulations, mobile health applications, and e-portfolios, reinforce these outcomes by providing immersive, interactive, and reflective learning experiences. Integrating narrative methods into digital platforms and curricular models presents a promising approach for linking clinical competence with relational care.
CONCLUSION:
The convergence of digital and narrative medicine offers a compelling pedagogical framework for healthcare education. This integrated approach supports both technological proficiency and humanistic values, enabling advancements in digital health to enhance rather than displace the interpersonal foundations of patient care. Further empirical research is needed to assess long-term outcomes and guide implementation in curricula, faculty development, and institutional policy.
2025-06-01·PHOTOCHEMICAL & PHOTOBIOLOGICAL SCIENCES
Uncovering the efficacy of a natural homemade sunscreen in protection from ultraviolet radiation
Article
作者: Stern, Harvey ; Dixon, Katie Marie ; Ince, Furkan Akif ; Nayar, Julianne Clare ; McClelland, James Andrew ; Holland, Andrew J A ; Mason, Rebecca Sara ; Abboud, Myriam ; Wong, Alicia Lauren
Abstract:
In Australia, skin cancer has the highest incidence of all cancer types, where Therapeutic Goods Association-approved, broad-spectrum sunscreens are recommended to prevent skin carcinogenesis. Commercial sunscreen ingredients, however, have been associated with negative impacts on human health, animal health and the environment. Together, the perceived harmful effects of commercial sunscreens have driven a trend towards home formulation of natural sunscreens, recipes for which are widely available online. Scientific evidence to support the efficacy of natural sunscreens, however, is lacking. We tested the efficacy of a natural homemade sunscreen (NHSS) published online by a wellness blogger with the aim to determine its photoprotective properties, beyond its ability to protect against erythema, compared to a commercially available SPF50 + sunscreen. The NHSS contained almond oil, coconut oil, shea butter, beeswax, red raspberry seed oil, carrot seed oil and zinc oxide. Skin explants were treated with either a commercial SPF50 + sunscreen, NHSS or base lotion prior to ultraviolet irradiation. Skin explants were assessed using immunohistochemistry for the levels of UVR-induced DNA damage in the form of cyclobutane pyrimidine dimers and 8-oxo-7, 8-dihydro-2’-deoxyguanosine, as well as for sunburn cells and epidermal thickness. We demonstrate herein that NHSSs can reduce UVR-induced DNA damage and epidermal thickness, but do not effectively protect against the generation of sunburn cells. In comparison, SPF50 + sunscreen provided effective protection against all investigated parameters. These factors, however, are markers of short-term UVR-induced damage and there is as yet no evidence for NHSSs in prevention of skin carcinogenesis. Therefore, we recommend the continued use of TGA-approved commercial sunscreens for sun protection. Further studies are required to test water resistance, variation in homemade formulation, shelf life, and protection against skin carcinogenesis in a chronic UVR model.Graphical Abstract
2025-03-01·ARTIFICIAL INTELLIGENCE IN MEDICINE
AI-based non-invasive imaging technologies for early autism spectrum disorder diagnosis: A short review and future directions
Review
作者: Weafer, Kate ; Contractor, Sohail ; Elnakib, Ahmed ; Shehata, Mohamed ; Abdelrahim, Mostafa ; Barnes, Gregory ; Ghazal, Mohammed ; Khudri, Mohamed ; Khalil, Ashraf ; Saleh, Gehad A ; El-Baz, Ayman ; Batouty, Nihal M
Autism Spectrum Disorder (ASD) is a neurological condition, with recent statistics from the CDC indicating a rising prevalence of ASD diagnoses among infants and children. This trend emphasizes the critical importance of early detection, as timely diagnosis facilitates early intervention and enhances treatment outcomes. Consequently, there is an increasing urgency for research to develop innovative tools capable of accurately and objectively identifying ASD in its earliest stages. This paper offers a short overview of recent advancements in non-invasive technology for early ASD diagnosis, focusing on an imaging modality, structural MRI technique, which has shown promising results in early ASD diagnosis. This brief review aims to address several key questions: (i) Which imaging radiomics are associated with ASD? (ii) Is the parcellation step of the brain cortex necessary to improve the diagnostic accuracy of ASD? (iii) What databases are available to researchers interested in developing non-invasive technology for ASD? (iv) How can artificial intelligence tools contribute to improving the diagnostic accuracy of ASD? Finally, our review will highlight future trends in ASD diagnostic efforts.
100 项与 Zayed University / Abu Dhabi 相关的药物交易
登录后查看更多信息
100 项与 Zayed University / Abu Dhabi 相关的转化医学
登录后查看更多信息
组织架构
使用我们的机构树数据加速您的研究。
登录
或

管线布局
2026年02月08日管线快照
无数据报导
登录后保持更新
药物交易
使用我们的药物交易数据加速您的研究。
登录
或
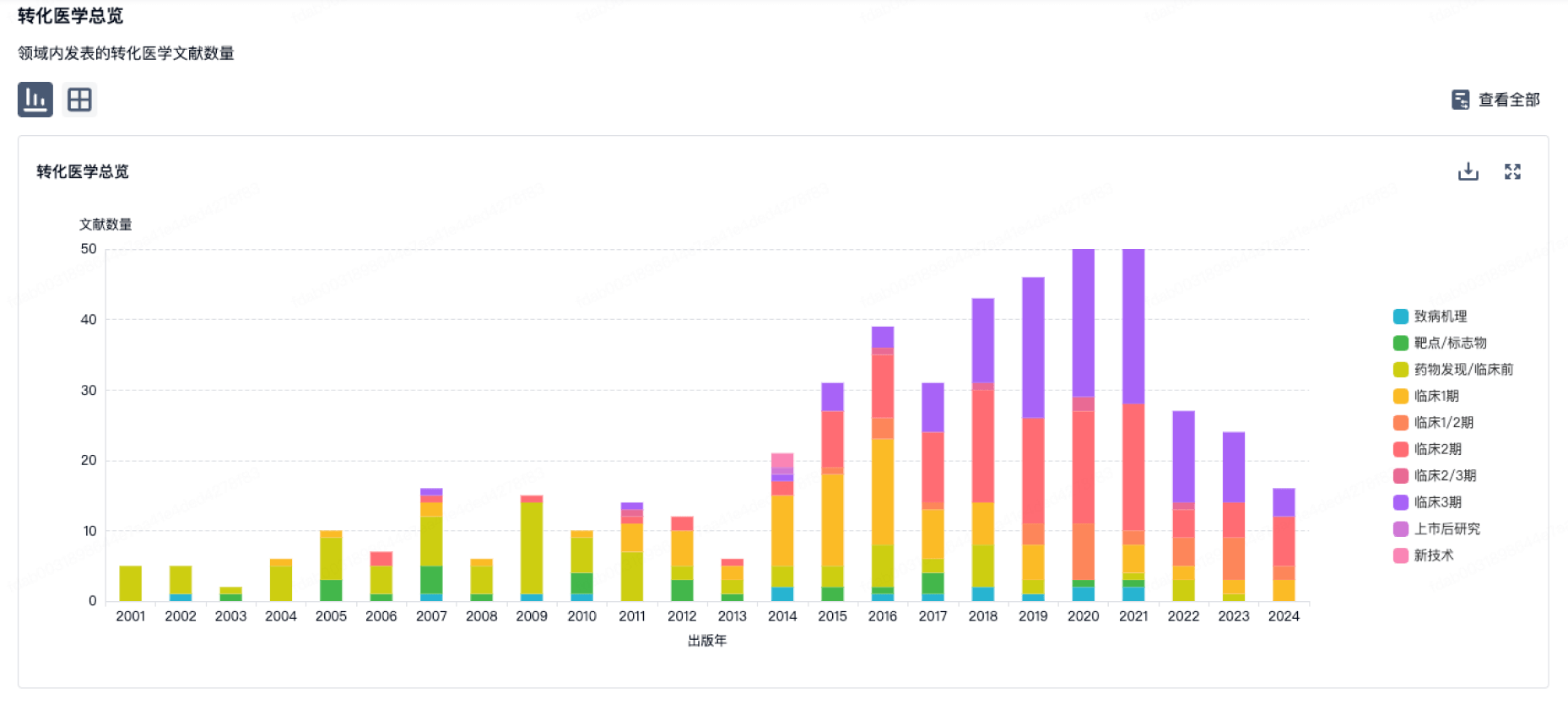
转化医学
使用我们的转化医学数据加速您的研究。
登录
或
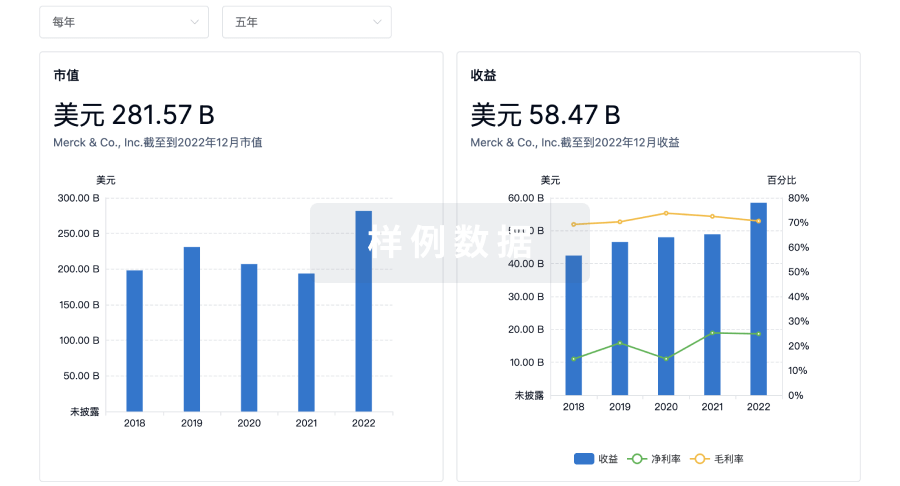
营收
使用 Synapse 探索超过 36 万个组织的财务状况。
登录
或
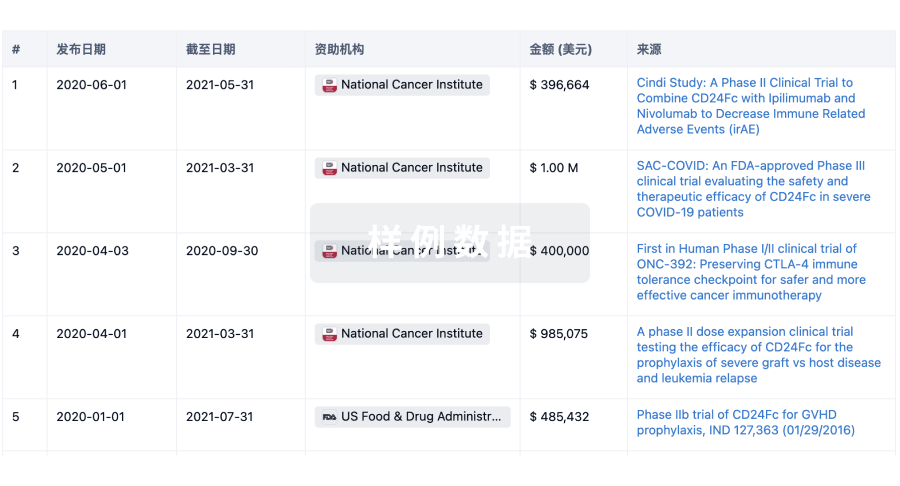
科研基金(NIH)
访问超过 200 万项资助和基金信息,以提升您的研究之旅。
登录
或
投资
深入了解从初创企业到成熟企业的最新公司投资动态。
登录
或
融资
发掘融资趋势以验证和推进您的投资机会。
登录
或
生物医药百科问答
全新生物医药AI Agent 覆盖科研全链路,让突破性发现快人一步
立即开始免费试用!
智慧芽新药情报库是智慧芽专为生命科学人士构建的基于AI的创新药情报平台,助您全方位提升您的研发与决策效率。
立即开始数据试用!
智慧芽新药库数据也通过智慧芽数据服务平台,以API或者数据包形式对外开放,助您更加充分利用智慧芽新药情报信息。
生物序列数据库
生物药研发创新
免费使用
化学结构数据库
小分子化药研发创新
免费使用