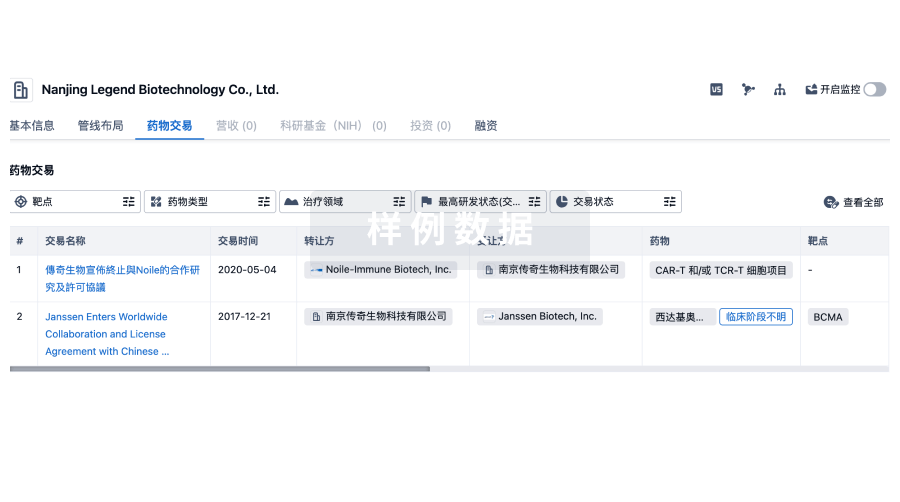
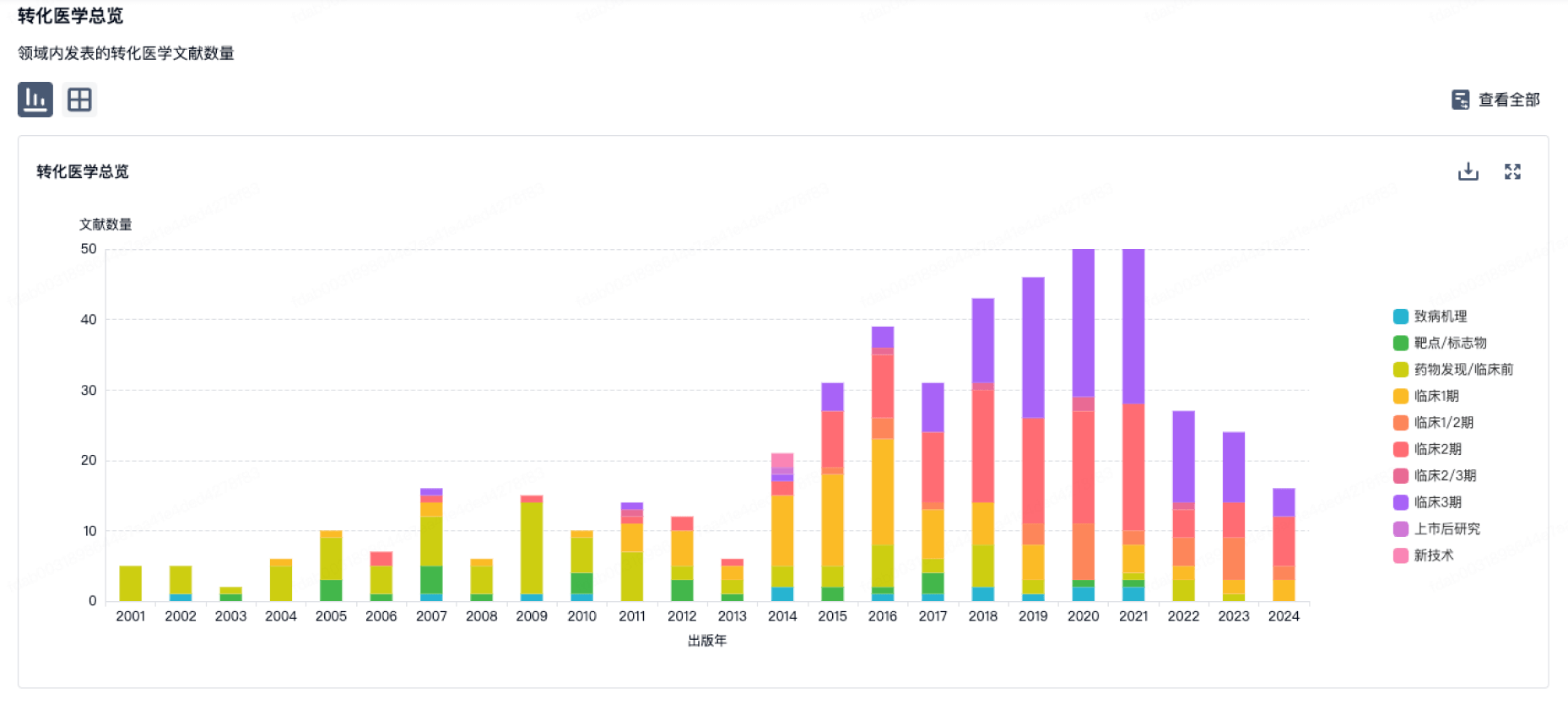
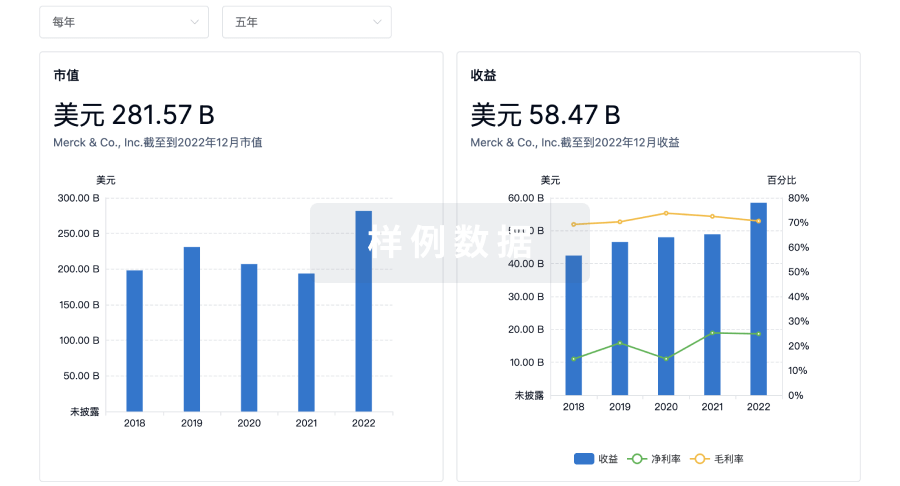
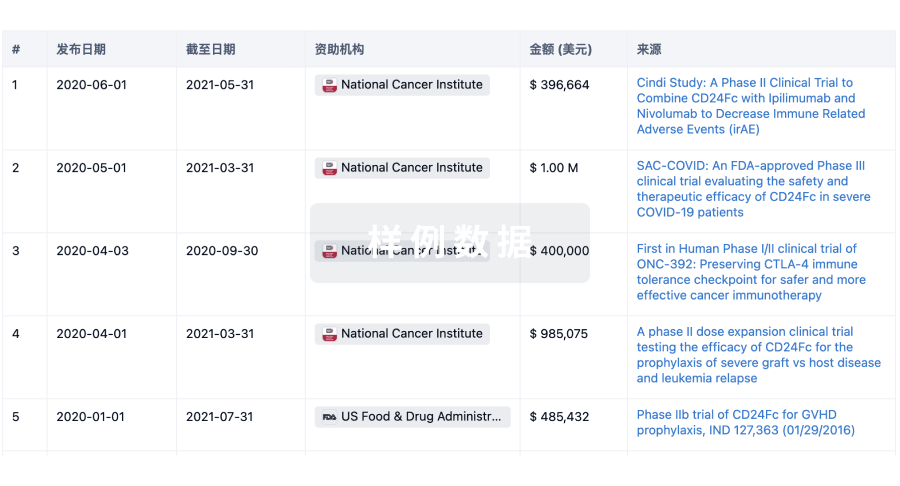
Abstract:This paper presents a method for the dynamic optimization of a chemical process, applicable whether or not the uncontrolled system is stable at the desired operating conditions. The system has several advantages over other methods of dynamic optimization: (1) Dimensionality is not a limitation; (2) Inequality constraints are handled directly; (3) A two‐point boundary value problem is not encountered; and (4) Control is designed around a stability criterion. Numerical results on a second order stirred‐tank reactor system are presented in order to verily the practicality of the proposed method.