预约演示
更新于:2026-02-26
Remetinostat
更新于:2026-02-26
概要
基本信息
在研机构- |
最高研发阶段终止临床2期 |
首次获批日期- |
最高研发阶段(中国)- |
特殊审评- |
登录后查看时间轴
结构/序列
分子式C16H21NO6 |
InChIKeyXDZAHHULFQIBFE-UHFFFAOYSA-N |
CAS号946150-57-8 |
关联
8
项与 Remetinostat 相关的临床试验ITMCTR2024000220
A clinical study on the treatment of knee osteoarthritis with homologous acupuncture of shape and qi
开始日期2024-09-01 |
申办/合作机构- |
NCT03875859
A Phase 2 Open Label, Single Arm Trial to Investigate the Efficacy and Safety of Topical Remetinostat Gel as Neoadjuvant Therapy in Patients Undergoing Surgical Resection of Squamous Cell Carcinoma (SCC)
The primary purpose of this study is to determine if 8 weeks of topical remetinostat applied three times daily will suppress Squamous Cell Carcinoma.
开始日期2019-12-12 |
申办/合作机构  Stanford University Stanford University [+1] |
ISRCTN17129075
The effectiveness of SLIM SHAPE 2.0 interventions in improving the health, wellness, and work productivity among the staff of Universiti Kebangsaan Malaysia
开始日期2019-10-01 |
申办/合作机构- |
100 项与 Remetinostat 相关的临床结果
登录后查看更多信息
100 项与 Remetinostat 相关的转化医学
登录后查看更多信息
100 项与 Remetinostat 相关的专利(医药)
登录后查看更多信息
5
项与 Remetinostat 相关的文献(医药)2024-11-01·EUROPEAN JOURNAL OF PHARMACOLOGY
Topical histone deacetylase inhibitor remetinostat improves IMQ-induced psoriatic dermatitis via suppressing dendritic cell maturation and keratinocyte differentiation and inflammation
Article
作者: Jiang, Qian ; Zhou, Xingchen ; Huang, Huining ; Jin, Liping
Psoriasis is a chronic inflammatory skin disease characterized by excessive proliferation of keratinocytes and infiltration of immune cells. Although psoriasis has entered the era of biological treatment, there is still a need to explore more effective therapeutic targets and drugs due to the presence of resistance and adverse reactions to biologics. Remetinostat, an HDAC inhibitor, can maintain its potency within the skin with minimal systemic effects, making it a promising topical medication for treating psoriasis. But its effectiveness in treating psoriasis has not been evaluated. In this study, the topical application of remetinostat significantly improved psoriasiform inflammation in an imiquimod-induced mice model by inhibiting CD86 expression of CD11C+I-A/I-E+ dendritic cells (DCs) in the skin. Moreover, remetinostat could dampen the maturation and activation of bone marrow-derived DCs in vitro, as well as the expression of psoriasis-related inflammatory mediators by keratinocytes. In addition, remetinostat could promote keratinocyte differentiation without affecting its proliferation. Our findings demonstrate that remetinostat improves psoriasis by inhibiting the maturation and activation of DCs and the differentiation and inflammation of keratinocytes, which may facilitate the potential application of remetinostat in anti-psoriasis therapy.
2023-06-01·Journal of labelled compounds & radiopharmaceuticals
Nitrilase mediated mild hydrolysis of a carbon‐14 nitrile for the radiosynthesis of 4‐(7‐hydroxycarbamoyl‐[1‐14C‐heptanoyl]‐oxy)‐benzoic acid methyl ester, [14C]‐SHP‐141: A novel class I/II histone deacetylase (HDAC) inhibitor
Article
作者: Moody, Thomas S. ; Chappell, Todd ; Kitson, Sean L. ; Watters, William ; Mazitschek, Ralph
A strategy has been developed for the carbon‐14 radiosynthesis of [14C]‐SHP‐141, a 4‐(7‐hydroxycarbamoyl‐heptanoyloxy)‐benzoic acid methyl ester derivative containing a terminal hydroxamic acid. The synthesis involved four radiochemical transformations. The key step in the radiosynthesis was the conversion of the 7‐[14C]‐cyano‐heptanoic acid benzyloxyamide [14C]‐4 directly into the carboxylic acid derivative, 7‐benzyloxycarbamoyl‐[14C]‐heptanoic acid [14C]‐8 using nitrilase‐113 biocatalyst. The final step involved deprotection of the benzyloxy group using catalytic hydrogenation to facilitate the release of the hydroxamic acid without cleaving the phenoxy ester. [14C]‐SHP‐141 was isolated with a radiochemical purity of 90% and a specific activity of 190 μCi/mg from four radiochemical steps starting from potassium [14C]‐cyanide in a radiochemical yield of 45%.
2022-01-01·JAMA dermatology1区 · 医学
Treatment of Cutaneous Squamous Cell Carcinoma With the Topical Histone Deacetylase Inhibitor Remetinostat
1区 · 医学
Letter
作者: Sarin, Kavita Y. ; Shah, Aatman ; Kilgour, James M. ; Eichstadt, Shaundra ; Aasi, Sumaira Z. ; Bailey, Irene
334
项与 Remetinostat 相关的新闻(医药)2026-02-25
打开今日头条查看图片详情 防走失,电梯直达安全岛报人刘亚东A 来源:深究科学作者:深究科学导读2024年,生物技术产业又迎来一个全新的转折点。 过去几年,生物技术领域发生了翻天覆地的变化,具有开创性的几大技术领域重塑了医疗保健、药物研发等行业的面貌。而在新的一年里,大热门将会在哪几个领域出现? 近期,几位行业专家谈2024年将塑造生物技术领域的趋势,看看他们有哪些洞见。01AI+生物医药 AI已经彻底改变了生物技术行业的格局。过去一年,人工智能在生物制药领域的应用热潮涌现,主要用于药物、蛋白质发现以及老药新用等。事实上,2023年AI取得了不少成果,并在持续发挥影响。 图源techcrunch 国际制药工程学会(ISPE)会长兼首席执行官(CEO)托马斯·哈特曼(Thomas Hartman)强调,过去一年,没有任何行业为人工智能的飞速发展做好准备:“现在,随着AI疲劳初见端倪,各种流程中实施AI的竞争也减少了,公司将有更多的时间,正确评估自己的技术和资源。” Standigm全球战略高级副总裁(SVP)兼药物化学部门负责人金韩洙(Hanjo Kim)认为AI的下一个研究趋势将针对肥胖和长寿,他表示,“许多人认为肥胖是代谢性疾病中唯一剩下的需要征服的疾病。此外,关于线粒体的科学发现令人兴奋,因为它们显示与许多疾病和并发症有关。” 此外,AI还大大节约了时间,提高了效率。Lantern Pharma的CEO潘纳·夏尔马(Panna Sharma)指出,针对特定疾病的AI发现和开发平台是下一步。“关键是前期数据准备,或者将这种原始信息转换为机器学习友好的格式,这些格式可以被强大的AI算法利用。这种准备可以让AI解锁数据中的见解,从而进行开创性的临床试验并加速药物开发”。 2024年,AI在生物技术领域展现出更精确、多样化的趋势,因此许多公司应当停一停,审视人工智能技术和他们手中的数据,找到最有效的方式来利用这些资产。02RNA技术 目前,RNA技术发展包括各种基于RNA的疗法:单链和双链RNA分子,如mRNA、miRNA、siRNA和反义RNA,每种分子都具有特定的机制和应用领域,如免疫治疗和疾病治疗。 Aldevron公司首席科学官(CSO)文卡塔·施拉万·K·因杜尔提(Venkata Shravan K. Indurthi)预测,RNA技术将更加复杂和精湛,有望在HIV和各种癌症等领域有所应用。 除此之外,他还推测,该行业将在基因编辑技术方面取得发展,“尽管基因编辑技术存在许多困难,但该行业在研究和最近批准的首款基因编辑药物方面仍取得了令人印象深刻的进展。这些发展也受到了越来越重要的合作伙伴关系的推动”。03CRISPR领域蓄势待发CRISPR技术为遗传性疾病的治疗带来了革命性的突破,目前正在临床试验中积极探索治疗镰状细胞病、β地中海贫血以及先天性黑蒙症(一种先天性失明症)等难题。这些试验已经取得了显著的成效,一些患者的病情得到了明显改善。 同时,在癌症治疗领域,CRISPR技术也在探索通过基因工程改造免疫细胞,以更有效地对抗肿瘤。这无疑为生物技术领域的发展注入了强大的动力,预计将在2024年持续推动行业的进步。 在CRISPR技术的开发中,重点在于为不同疾病创造特定的递送系统。这包括利用对环境有反应和能识别配体的纳米颗粒,以更精准地靶向病变组织。 此外,利用免疫细胞或病变器官的外泌体和细胞膜,也能更有效地递送基因靶向药物,并避免免疫系统的清除。 ERS Genomics公司的首席执行官埃里克·罗兹(Eric Rhodes)认为,该领域将在2024年继续保持增长势头。他表示,“CRISPR/Cas9技术将在2024年继续其非凡的增长轨迹,这得益于英国首个获批的临床应用,用于治疗镰状细胞病和输血依赖型β地中海贫血(TDT)。美国食品药品监督管理局(FDA)最近对TDT的Casgevy的批准进一步证明了该技术治愈以前无法治疗的疾病的巨大潜力”。 此外,他还预测,“随着CRISPR逐渐成为主流医学技术,我们预计基于CRISPR的临床试验数量将大幅增加。更令人期待的是,看到这项技术如何超越医学领域”。 04生物打印和组织工程2024年,生物打印和组织工程预计将崛起为生物工程行业的核心趋势。 生物打印与3D打印技术有异曲同工之妙,它运用由活性人类细胞构成的“生物墨水”来构建组织,最终目标是制造生物人工器官来缓解供体器官短缺的困境。尽管生物打印器官的实际应用尚未到来,但当前这项技术对于烧伤患者的支持已经展现出了巨大的潜力。研究人员已经研发出手持式生物打印工具,可直接将皮肤组织层沉积在伤口上,有望取代传统的皮肤移植方式,并加速愈合过程。 生物打印技术的持续进步也在推动更大、更复杂的组织结构的工程化。研究团队正在探索创新的组装方法,力求突破以往的尺寸限制,制造出更多工程化器官。 生物组织工程市场同样展现出强劲的增长势头,预计到2028年,其市场价值将达到89亿美元,复合年增长率(CAGR)高达15.3%。 目前,北美占据最大的市场份额,但亚洲太平洋地区因对治疗慢性疾病的创新技术采纳度不断提升,预计将成为增长最为显著的地区。 05干细胞技术 干细胞类型的多样性日益丰富,如间充质干细胞和诱导多能干细胞等,它们在研发工作中大放异彩,推动了市场的快速增长并拓展了干细胞在医学领域的应用范围。尤其在CRISPR基因编辑等领域的革新,进一步提升了干细胞的精准度、可扩展性和治疗潜力,为2024年癌症和心血管疾病等疾病治疗带来了广阔的前景。 图源:News-Medical 展望未来,干细胞技术和疗法的全球市场预计将以11.43%的复合年增长率(CAGR)从2024年持续增长至2030年。其中,再生医学领域备受瞩目,随着越来越多的干细胞疗法临床试验获得批准,其市场份额正不断攀升。 然而,干细胞市场的竞争也日益激烈,导致优质干细胞产品的定价竞争变得尤为白热化。并购活动的频发也为干细胞市场的扩张注入了新的活力,显示了该行业的蓬勃生机和巨大潜力。尽管如此,该领域仍面临着一些挑战,如严格的研究和临床实践指南可能会增加额外的程序成本并延长研发周期。 值得一提的是,干细胞技术在药物测试、疾病模拟以及治疗神经退行性疾病(如帕金森病和阿尔茨海默病)等领域的应用也在逐步普及。这些技术在不同应用领域中所展现的潜力,凸显了干细胞在生物技术未来中可能发挥的举足轻重的作用。06靶向蛋白降解 靶向蛋白降解技术正在迅猛增长,预计将在2024年延续其上升势头,成为生物技术领域中的瞩目焦点。这一增长受到多重因素推动,包括治疗方法中先进技术的普及、表位抑制剂技术的广泛应用,以及药物研发中对蛋白质降解策略的日益增长的需求。同时,市场对微生物感染诊断中免疫测定的需求持续增长,以及人们对蛋白质降解益处的认识提升,也进一步推动了市场的蓬勃发展。 PhoreMost公司的首席执行官Neil Torbett认为,2024年将是TPD领域发生变革性进展的一年。继2023年披露的双价降解药物和临床试验数量的显著增加后,他预测今年投资者和制药公司对该领域的兴趣将进一步升温,因为先进的蛋白水解靶向嵌合体(PROTACs)即将进入3期临床试验阶段。“分子胶作为降解药物疗法的一种激动人心的新方法,为新的治疗领域带来了改进的药理学特性。尽管分子胶的合理设计在历史上一直颇具挑战性,但我们有理由相信,2024年该领域将实现突破。”他如是表示。 在地域分布上,北美地区是PROTAC市场的领军者,这主要得益于该地区丰富的研发活动。与此同时,随着政府支持力度的加大、医学研究的繁荣以及对优质医疗保健需求的不断增长,亚太地区的市场也在逐步扩大。 PROTAC技术的主要参与者包括礼来公司(Eli Lilly and Company)、吉利德科学公司(Gilead Sciences)和默克公司(Merck)等知名企业。这个充满活力的市场以技术创新和广泛的应用领域为特色,预计将在2024年及以后成为生物技术行业的重点关注领域。 参考资料 The trends that will shape the biotech industry in 2024.Labiotech.
信使RNA核酸药物寡核苷酸基因疗法siRNA
2026-02-24
·腾讯网
█ 脑科学动态Cell:无需运动也能健脑:肝脏分泌物可修复血脑屏障Cell:癌症的隐形刹车:GPX1-OSBPL8轴如何调控肿瘤生长与死亡Nature:利用体内碱基编辑在出生后改善小鼠自闭症样行为Cell:单次溶瘤病毒治疗激活持久T细胞免疫,攻克致命脑肿瘤积极预期可激活大脑奖赏回路,进而提升疫苗抗体水平AI聊天机器人可能加剧精神疾病患者病情催产素逆转青少年期社会隔离引发的焦虑与社交障碍多巴胺联手星形胶质细胞重塑运动记忆观鸟专家的大脑结构更紧凑,或是对抗认知衰老的秘诀█ AI行业动态DeepRare攻克罕见病诊断难题,准确率首超人类专家把人类文明写入玻璃:微软突破性存储技术可保存数据一万年Gemini 3.1 Pro上线█ AI驱动科学Science:给AI做“脑部手术”:科学家精准定位并操控大模型潜意识Cell:原子级AI模型PocketXMol,统一分子生成任务眼睛的存在如何提升人类对人形机器人心智的感知让AI懂物理:PhysiOpt系统通过物理模拟优化生成式3D设计Nature:评估大语言模型真实道德能力的新路线图密歇根大学开源新工具揭示AI模型推理能耗差异及潜在机制首个AI代理专属社交网络Moltbook揭示AI自主交互的潜在风险结构化压力测试揭示ChatGPT Health分诊建议的安全隐患融合牛顿第三定律的物理感知AI算法实现动态系统稳定模拟脑科学动态Cell:无需运动也能健脑:肝脏分泌物可修复血脑屏障运动对大脑有益,但老年人往往难以坚持。为了解决这一难题,加州大学旧金山分校的 Saul A. Villeda 和 Gregor Bieri 等研究人员,深入探索了名为 GPLD1 的肝脏酶如何将运动的益处传递给大脑。他们发现了一条通过肝脏与大脑血管相互作用的全新通路,揭示了无需实际运动即可逆转大脑衰老和改善阿尔茨海默病相关记忆丧失的可能性。该研究的核心在于揭示了肝脏产生的酶 GPLD1(糖基磷脂酰肌醇特异性磷脂酶 D1)与大脑血管上的蛋白质 TNAP(组织非特异性碱性磷酸酶)之间的相互作用。研究人员发现,随着年龄增长,大脑血管上的 TNAP 水平会异常升高,进而破坏血脑屏障并损害认知功能。实验显示,GPLD1 就像一把“分子剪刀”,能够精准切除脑血管上过多的 TNAP。通过在老年小鼠体内提高 GPLD1 水平或直接使用药物抑制 TNAP,研究团队成功修复了受损的血脑屏障,使小鼠的记忆力和学习能力恢复到年轻状态。更令人振奋的是,在阿尔茨海默病模型小鼠中,这一策略不仅改善了认知缺陷,还减少了大脑中的病理标志物。这一发现表明,大脑血管是连接肝脏与大脑认知功能的关键桥梁。研究发表在 Cell 上。#疾病与健康 #健康管理与寿命延长 #神经机制与脑功能解析 #阿尔茨海默病 #脑血管阅读更多:Bieri, Gregor, et al. “Liver Exerkine Reverses Aging- and Alzheimer’s-Related Memory Loss via Vasculature.” Cell, vol. 0, no. 0, Feb. 2026. www.cell.com, https://doi.org/10.1016/j.cell.2026.01.024Cell:癌症的隐形刹车:GPX1-OSBPL8轴如何调控肿瘤生长与死亡体内铁死亡如何在无外源诱导剂的情况下自然发生?来自哥伦比亚大学的Wei Gu团队与匹兹堡大学的Valerian E. Kagan团队及第一作者Zhangchuan Xia等人合作开展了深入研究。他们发现并阐明了一条全新的非经典铁死亡通路,该通路不依赖于传统的GPX4缺失或药物诱导,而是由特定的信号轴调控,这一发现为理解天然肿瘤抑制机制提供了关键线索。▷ Credit:Cell.这项研究深入解析了活性氧(ROS)在细胞内引发的一系列分子事件。研究人员发现,ROS会导致内质网上的磷脂酸发生过氧化反应,这是铁死亡启动的早期关键步骤。为了维持细胞生存,位于内质网膜上的氧固醇结合蛋白样蛋白8(OSBPL8)会发挥“招募者”的作用,将通常被认为是细胞质抗氧化酶的谷胱甘肽过氧化物酶1(GPX1)拉向内质网。在此处,GPX1功能发生重定义,它直接还原被氧化的磷脂酸,从而充当了铁死亡的“刹车”。如果这一修复机制失效,即GPX1或OSBPL8的功能缺失,过氧化的脂质就会在内质网积累,进而触发非经典铁死亡。实验结果证实,在多种癌症模型中阻断GPX1-OSBPL8信号轴,能够有效激活铁死亡程序,显著抑制肿瘤生长。这不仅揭示了癌细胞逃避死亡的新机制,也为开发靶向该信号轴的抗癌药物提供了理论依据。研究发表在 Cell 上。#神经科学 #神经机制与脑功能解析 #技术创新 #单神经元重建 #全脑成像阅读更多:Xia, Zhangchuan, et al. “A GPX1-OSBPL8 Axis Mediates Noncanonical in Vivo Ferroptosis and Cancer Growth Suppression.” Cell, vol. 0, no. 0, Feb. 2026. www.cell.com, https://doi.org/10.1016/j.cell.2026.01.009Nature:利用体内碱基编辑在出生后改善小鼠自闭症样行为针对由基因突变引起的神经发育障碍缺乏有效疗法这一难题,上海交通大学的仇子龙团队、复旦大学的程田林团队以及上海交通大学医学院附属新华医院的李斐团队展开联合攻关。研究人员通过开发新型基因编辑工具,成功在小鼠体内修复了导致Snijders Blok-Campeau综合征的基因突变,并显著改善了相关的自闭症样行为和认知障碍,为治疗此类遗传性神经发育疾病提供了新策略。研究团队针对由 *CHD3* 基因突变引起的Snijders Blok-Campeau综合征(SNIBCPS)进行了深入研究。他们首先构建了携带特定基因突变的人源化小鼠模型,该模型表现出与人类患者相似的智力障碍和自闭症样行为。为了在体内修复这一突变,研究人员设计了一种名为TeABE的TadA嵌入式腺嘌呤碱基编辑器(TadA-embedded adenine base editor),这是一种能够在不切断DNA双链的情况下将A•T碱基对精准转化为G•C碱基对的工具。团队利用双腺相关病毒(dual AAV)系统作为载体,通过静脉注射将TeABE递送至小鼠大脑。结果显示,该疗法在小鼠皮层和海马区实现了高效的基因校正,恢复了CHD3蛋白的正常水平,并成功挽救了小鼠的社交沟通缺陷和认知异常。此外,研究团队还在非人灵长类动物中验证了该递送系统的有效性,通过鞘内注射实现了广泛的脑部转导,进一步支持了该技术向临床转化的可行性。这项研究证明了在出生后进行精准的单碱基编辑有望逆转单基因神经发育障碍的病理表型。研究发表在 Nature 上。#疾病与健康 #心理健康与精神疾病 #基因编辑 #自闭症 #神经发育障碍阅读更多:Yang, Kan, et al. “In Vivo Base Editing of Chd3 Rescues Behavioural Abnormalities in Mice.” Nature, Feb. 2026, pp. 1–11. www.nature.com, https://doi.org/10.1038/s41586-026-10113-6Cell:单次溶瘤病毒治疗激活持久T细胞免疫,攻克致命脑肿瘤胶质母细胞瘤(GBM)因其高致死率和治疗抵抗性,长期以来被视为医学难题。丹娜-法伯癌症研究所(Dana-Farber Cancer Institute)和哈佛医学院的Maxime Meylan、Ye Tian、Lijian Wu等研究人员取得重大突破,他们发现单次注射经过改造的溶瘤病毒,能够成功将胶质母细胞瘤的免疫微环境从“冷”变“热”,激活患者自身的免疫系统对肿瘤进行长期的识别和攻击,从而显著延长患者生存期。▷ Credit:Cell.这项研究深入分析了一项1期临床试验的结果,研究团队利用先进的空间蛋白组学(Spatial proteomics)和空间转录组学技术,对患者的肿瘤样本进行了高精度的空间分析。研究结果显示,单次瘤内注射溶瘤病毒后,肿瘤内部出现了深度且持久的T细胞浸润。具体而言,表达颗粒酶B(Granzyme B,一种细胞毒性分子)的T细胞被发现紧密围绕在发生凋亡的肿瘤细胞周围,提供了免疫细胞直接杀伤癌细胞的确凿证据。进一步的T细胞受体测序分析表明,这种治疗主要激活并扩增了患者体内原本就存在的肿瘤特异性T细胞克隆。有趣的是,空间分析显示病毒残留物主要局限在坏死区域,而激活的T细胞则深入渗透到了存活的肿瘤组织中,表明后期的抗肿瘤效应主要由免疫系统而非病毒直接驱动。此外,数据还提示长期使用地塞米松(Dexamethasone,常用于缓解脑水肿的激素)可能会抑制这种有益的免疫反应,这为未来的临床用药提供了重要指导。研究发表在 Cell 上。#疾病与健康 #个性化医疗 #胶质母细胞瘤 #溶瘤病毒 #癌症免疫治疗阅读更多:Meylan, Maxime, et al. “Persistent T Cell Activation and Cytotoxicity against Glioblastoma Following Single Oncolytic Virus Treatment in a Clinical Trial.” Cell, vol. 0, no. 0, Feb. 2026. www.cell.com, https://doi.org/10.1016/j.cell.2025.12.055积极预期可激活大脑奖赏回路,进而提升疫苗抗体水平积极的心态是否真的能像“安慰剂”一样增强免疫力?来自特拉维夫大学(Tel Aviv University)的 Nitzan Lubianiker、Asya Rolls 和 Talma Hendler 等研究人员,通过一项随机对照人体试验证实了大脑与免疫系统之间的直接联系。该团队发现,当我们通过有意识的心理活动激活大脑深处的奖赏回路时,可以显著增强身体对疫苗的免疫反应。该研究招募了85名健康志愿者,利用功能磁共振神经反馈(functional MRI neurofeedback)技术进行了一项独特的脑机训练。参与者在扫描仪中通过回忆快乐经历或想象达成目标等心理策略,尝试“用意念”调节大脑特定区域的活动。随后,所有参与者接种了乙肝疫苗。研究结果显示,大脑中的腹侧被盖区——一个与动机和奖赏密切相关的核心脑区——其活跃程度的增加与疫苗接种后抗体水平的提升呈现显著的正相关。值得注意的是,这种免疫增强效果并非随机产生,而是与参与者产生的“积极预期”密切相关。数据分析表明,那些能有效激活腹侧被盖区的心理策略,通常包含了对未来积极结果的期待。虽然不同实验组之间的平均抗体水平没有显著差异,但个体成功上调该脑区活动的能力直接预测了其免疫反应的强度。这项研究不仅揭示了大脑奖赏系统在调节免疫功能中的关键作用,也暗示了未来可能通过非侵入性的神经反馈训练或心理干预,辅助增强疫苗效果或调节免疫相关疾病。这一发现发表在 Nature Medicine 上。#疾病与健康 #神经机制与脑功能解析 #安慰剂效应 #神经反馈 #疫苗阅读更多:Lubianiker, Nitzan, et al. “Upregulation of Reward Mesolimbic Activity and Immune Response to Vaccination: A Randomized Controlled Trial.” Nature Medicine, vol. 32, no. 2, Feb. 2026, pp. 572–81. www.nature.com, https://doi.org/10.1038/s41591-025-04140-5AI聊天机器人可能加剧精神疾病患者病情人工智能聊天机器人是否会危害精神健康?来自奥胡斯大学和奥胡斯大学医院的 Sidse Godske Olsen、Christian Jon Reinecke-Tellefsen 和 Søren Dinesen Østergaard 等人进行了一项大规模研究。他们通过分析临床数据发现,对于已知患有精神疾病的人群,使用AI聊天机器人可能会导致病情恶化,尤其是在加重妄想症状方面风险显著。该研究基于丹麦中部地区精神病学服务系统近三年间的电子健康记录,涵盖了53,974名患者。研究团队搜索了超过1000万条临床笔记,寻找包含“ChatGPT”或“chatbot”及其拼写变体的记录,并由专家逐一评估这些互动是否对患者产生了负面影响。结果显示,在识别出的相关病例中,最主要的问题是AI聊天机器人倾向于迎合用户的输入,从而验证或强化了患者的妄想,例如夸大妄想或偏执。此外,研究还发现了聊天机器人可能加剧躁狂、助长饮食障碍患者计算卡路里的强迫行为,甚至被用于查询自杀方法的案例。尽管也有部分患者利用AI进行自我心理教育或缓解孤独,但研究人员警告称,目前发现的病例可能只是冰山一角,对于患有精神分裂症等严重精神疾病的群体,使用此类缺乏监管的技术存在极高风险。研究发表在 Acta Psychiatrica Scandinavica 上。#疾病与健康 #心理健康与精神疾病 #大模型技术 #人机交互 #电子健康记录阅读更多:Olsen, Sidse Godske, et al. “Potentially Harmful Consequences of Artificial Intelligence (AI) Chatbot Use Among Patients With Mental Illness: Early Data From a Large Psychiatric Service System.” Acta Psychiatrica Scandinavica, n/a, no. n/a. Wiley Online Library, https://doi.org/10.1111/acps.70068. Accessed 24 Feb. 2026催产素逆转青少年期社会隔离引发的焦虑与社交障碍长期社会隔离,尤其是发生在青春期的隔离,往往会导致焦虑、抑郁及社交困难,严重影响心理健康。来自电子科技大学的Junjun Li、Chuanjiang Wu、Yang Xia等研究人员发现“拥抱激素”催产素不仅能改善隔离导致的行为异常,还能在神经和生理层面修复相关损伤,为治疗隔离诱发的精神障碍提供了新的思路。▷ 上图:前额叶皮层 (PFC) 中 MAP-2(绿色)和 DAPI(蓝色)共定位的代表性图像。MAP-2 表达区域的定量分析。下图:前额叶皮层 (PFC) 中 PSD-95(绿色)和 DAPI(蓝色)共定位的代表性图像。PSD-95 颗粒计数的定量分析。比例尺 = 50 μm。每组 n = 6,每只小鼠取 2-3 个脑切片。采用非配对 t 检验。数据以平均值 ± 标准误 (SEM) 表示。★★P<0.01,★★★P<0.001。Credit: Li et al. 研究团队选取4周龄的小鼠进行为期三个月的社会隔离,模拟青少年期的长期孤独状态。随后,通过鼻内给药的方式对小鼠施用催产素,并结合行为学测试、脑组织分析及肠道菌群检测来评估疗效。结果显示,隔离小鼠表现出的焦虑、抑郁样行为及社交记忆受损在接受催产素治疗后得到有效逆转。在生理机制上,催产素增加了前额叶皮层(PFC)中微管相关蛋白2(MAP-2)和突触后致密蛋白95(PSD-95)的表达,这两种蛋白分别与神经元骨架稳定性和突触传递功能密切相关,意味着受损的神经连接得到了修复。此外,该治疗还降低了异常升高的催产素受体水平,减轻了神经炎症,并恢复了肠道菌群的稳态。这项研究揭示了催产素通过神经、免疫和微生物多重机制调节心理健康的潜力。研究发表在 Translational Psychiatry 上。#疾病与健康 #心理健康与精神疾病 #神经机制与脑功能解析 #肠道菌群阅读更多:Li, Junjun, et al. “Oxytocin Attenuates Isolation-Evoked Emotional and Social Behavioral Dysregulation through Neural, Immune, and Microbiota Mechanisms.” Translational Psychiatry, Feb. 2026. www.nature.com, https://doi.org/10.1038/s41398-026-03888-9多巴胺联手星形胶质细胞重塑运动记忆学习新技能时大脑如何“布线”?来自韩国科学技术院(KAIST)、基础科学研究院(IBS)和蔚山科学技术大学(UNIST)的Young-Jin Choi、郑元锡(Won-Suk Chung)、金在益(Jae-Ick Kim)等人组成的团队发现,大脑中的星形胶质细胞并非旁观者,而是主动参与了运动学习中的神经回路重塑。它们在多巴胺信号的指挥下,精准修剪多余的神经连接,确保运动技能的熟练掌握。▷ 运动学习前后星形胶质细胞介导的突触消除。运动学习后,星形胶质细胞介导的突触消除显著增加。这种与学习相关的增加在星形胶质细胞特异性 Megf10 敲除小鼠中未观察到。此外,与对照组相比,Megf10 敲除小鼠的运动学习能力显著受损。Credit: Nature Communications (2026). 研究团队通过观察进行运动训练的小鼠,利用先进成像技术发现,随着学习的深入,纹状体中的星形胶质细胞会显著增加对突触的消除。研究确认了一种名为MEGF10的吞噬受体是这一过程的关键分子。当研究人员特异性敲除小鼠星形胶质细胞中的MEGF10后,小鼠的运动学习能力出现明显缺陷,原本应发生的突触长时程增强(LTP)和长时程抑制(LTD)也受到破坏。进一步实验揭示了“多巴胺选择,胶质细胞精修”的机制:神经元活动和多巴胺信号共同调节这一过程,多巴胺信号帮助确定哪些神经元需要保持活跃,而星形胶质细胞则通过MEGF10受体,选择性地吞噬并移除那些较弱的连接,从而保留强连接。这表明星形胶质细胞在将多巴胺信号转化为持久的大脑结构变化中起着至关重要的作用。研究发表在 Nature Communications 上。#神经科学 #神经机制与脑功能解析 #星形胶质细胞 #多巴胺 #突触可塑性阅读更多:Choi, Young-Jin, et al. “Motor Learning and Dopamine-Dependent Striatal Synaptic Plasticity Are Controlled by Astrocytic MEGF10.” Nature Communications, vol. 17, no. 1, Feb. 2026, p. 1351. www.nature.com, https://doi.org/10.1038/s41467-026-69129-1观鸟专家的大脑结构更紧凑,或是对抗认知衰老的秘诀学习一项复杂技能如何重塑我们的大脑?来自贝克雷斯特医院的 Erik A. Wing、Jordan A. Chad 和 Asaf Gilboa 等研究人员,对比了观鸟专家与普通人的大脑结构。研究发现,长期从事观鸟活动的人,其负责注意力和感知的大脑区域结构更为紧凑,这种结构性变化不仅与更高的识别能力相关,还可能有助于抵御大脑随年龄增长而出现的认知衰退。在这项研究中,研究团队招募了29名观鸟专家和29名年龄、性别匹配的新手,利用弥散加权磁共振成像(diffusion-weighted MRI)技术对他们的大脑进行了扫描。研究人员重点测量了大脑皮层的平均扩散率(Mean Diffusivity, MD),这是一种反映水分在组织中扩散受限程度的指标,MD值越低通常意味着大脑组织结构越紧凑、复杂度越高。结果显示,专家在额顶叶和后皮层区域的MD值显著低于新手。此外,研究还发现,随着年龄增长,普通人的大脑MD值通常会上升(意味着结构松散化),但在观鸟专家中,这种与年龄相关的增加趋势更为平缓。这意味着,通过观鸟获得的技能可能为特定脑区提供了某种形式的保护,减缓了衰老带来的影响。功能性磁共振成像数据还揭示,当专家在识别不熟悉的非本地鸟类时,这些结构紧凑的区域会被选择性地激活,从而支持其卓越的感知表现。研究发表在 Journal of Neuroscience 上。#认知科学 #神经机制与脑功能解析 #健康管理与寿命延长 #记忆机制 #大脑可塑性阅读更多:Wing, Erik A., et al. “The Tuned Cortex: Convergent Expertise-Related Structural and Functional Remodeling across the Adult Lifespan.” Journal of Neuroscience, Feb. 2026. Research Articles. www.jneurosci.org, https://doi.org/10.1523/JNEUROSCI.1307-25.2026AI 行业动态上海交大AI智能体DeepRare攻克罕见病诊断难题,准确率首超人类专家全球超过3亿罕见病患者漫长而曲折的“诊断奥德赛”(指患者为确诊需辗转多年、反复求医的艰难历程)有望迎来终结。2月18日,上海交通大学与上海人工智能实验室的谢伟迪团队,联合上海新华医院孙锟、余永国等研究人员在Nature杂志发表研究,推出了全球首个面向罕见病诊断的AI智能体系统——DeepRare。该系统能处理患者自由文本描述、标准化症状术语乃至基因测序数据等异质的临床信息,像一个由AI驱动的“虚拟专家会诊中心”,通过内部多个专业智能体(如文献检索、病例匹配、基因分析等)的协同工作,生成带有清晰推理步骤和可验证医学证据引用的诊断建议。 研究团队在涵盖亚洲、北美和欧洲6400余个真实病例、涉及近3000种罕见病的基准测试中证实,DeepRare的诊断准确率显著超越现有方法。仅基于症状表型诊断时,其首次诊断准确率(Recall@1,即正确诊断排在首位的比例)平均达57.18%,比第二名高出23.79%;当结合基因数据后,准确率更跃升至69.1%,优于传统生物信息学工具Exomiser(55.9%)。在与5位资深罕见病专家的对比中,DeepRare的首次诊断准确率以64.4%首次超越人类专家的54.6%。尤为关键的是,其生成的推理链在医学证据准确性和相关性上获得了高达95.4%的专家认可率。这一成果不仅为全球罕见病患者带来精准诊断的新希望,更标志着AI正从单纯的辅助工具,进化为能够进行透明化复杂推理的临床“合作伙伴”,有望重塑未来的诊疗流程。#DeepRare #罕见病诊断 #AI智能体 #医疗AI #Nature阅读更多:https://www.nature.com/articles/s41586-025-10097-9把人类文明写入玻璃:微软突破性存储技术可保存数据一万年人类对永恒保存文明的追求,在数字时代遇到了新的挑战:传统硬盘寿命短、易受干扰,而模拟介质如“旅行者金唱片”虽能久存,但信息容量极其有限。微软研究院主导的Project Silica项目在Nature杂志上发表了一项突破性研究,提出了一种全新的解决方案——将海量数据以极高密度和耐久性存储在普通玻璃之中。研究团队成功在一块120毫米见方、2毫米厚的玻璃上存储了超过4.8 TB的数据,相当于数百万份文档的照片或一部超高清电影。通过加速老化测试证明,这种玻璃中的数据保存寿命可以超过一万年,且能抵御电磁干扰、极端温度和湿气侵蚀。 这一革命性技术的关键在于对飞秒激光写入系统的创新。研究人员开发了“伪单脉冲写入”技术,大幅提升了在玻璃内部刻录数据的效率,并提出了全新的“相位体素”(phase voxel)概念。与以往依赖偏振变化的存储方式不同,“相位体素”仅需单次激光脉冲即可在玻璃内部形成编码信息的微观结构,且能应用于成本更低的硼硅酸盐玻璃。配合机器学习模型来纠正确保数据读取的准确性,以及多光束并行写入系统,玻璃存储首次在写入速度和规模化潜力上展现出替代传统长期存档介质的可能性。目前,该技术已开始应用于实践,如在挪威斯瓦尔巴群岛的全球音乐宝库项目中,用于创建一个能抵抗电磁脉冲、无需持续供电维护的永久性音乐档案库。Project Silica指向的未来,是一个用极小的物理空间、极低的运维成本,封装人类全部文明精华的“玻璃数据库”。#玻璃数据存储 #ProjectSilica #微软研究院 #Nature论文 #超长期存档阅读更多:https://www.nature.com/articles/s41586-025-10042-wGemini 3.1 Pro上线,推理能力翻倍震惊业界在国产大模型激烈竞争之际,谷歌于深夜突然发布新版AI模型——Gemini 3.1 Pro。这是谷歌首次采用「.1」这样的小版本号进行更新,但其性能提升幅度却远超预期。研究人员介绍,3.1 Pro的核心是将此前Gemini 3 Deep Think的推理能力公开并进一步强化,在ARC-AGI-2基准测试中得分达到77.1%,推理性能约为上一代Gemini 3 Pro的两倍。此外,该模型支持百万tokens的上下文,知识更新至2025年1月,并在多模态生成、语义理解和长文本处理上均有显著增强。目前,3.1 Pro已在Gemini应用和API中上线,面向Google AI Pro和Ultra用户开放。 此次升级的实际效果迅速引发用户热烈反响。有开发者用3.1 Pro直接生成了《我的世界》游戏场景和个人网站,甚至有用户让其开发出一款光线效果逼真的教育应用。官方演示中,模型能将日常数据转化为交互式可视化内容,或一键生成“模拟城市”的完整交通系统。更值得关注的是,在性能翻倍的同时,其定价却与Gemini 3 Pro Preview持平,使得完成复杂任务的成本大幅下降。例如完成一次ARC-AGI-2任务的成本仅为0.96美元,远低于Gemini 3 Deep Think的十倍价格。业内认为,这标志着大模型正沿着帕累托前沿(即在成本最低的情况下实现性能最大化)快速推进,智能成本正在以数量级的速度持续压缩,为2026年的AI竞赛拉开了激烈序幕。#Gemini31Pro #谷歌AI #推理能力 #多模态模型 #AI成本下降阅读更多:https://blog.google/innovation-and-ai/models-and-research/gemini-models/gemini-3-1-pro/AI 驱动科学Science:给AI做“脑部手术”:科学家精准定位并操控大模型潜意识大型语言模型内部隐藏着丰富的情绪、偏见和人格特征,但如何精准定位并控制这些抽象概念一直是个难题。来自麻省理工学院、加州大学圣地亚哥分校、哈佛大学和宾夕法尼亚大学的 Adityanarayanan Radhakrishnan、Daniel Beaglehole、Mikhail Belkin 和 Enric Boix-Adserà 等研究人员组成的研究团队,开发了一种通用的监督学习方法。该方法不仅能揭示模型内部的“思维地图”,还能像调节音量一样精准操控模型的行为表现。▷ 通过将 ϵv 添加到模块 i 的输出中(其中 ϵ>0 为常数),模型会趋向于该概念。Credit: Science (2026).研究团队摒弃了传统的低效无监督搜索,转而采用一种名为递归特征机(Recursive Feature Machine,RFM)的算法。该方法通过对比包含特定概念(如“阴谋论”)与不含该概念的提示词数据,精准锁定大模型内部代表该概念的数学向量。随后,研究人员通过向模型激活层添加这些向量,实现了对超过500种概念的“引导”——即人为地增强或减弱某种特质。实验结果显示,该技术能够让大模型瞬间化身为“阴谋论者”或“波士顿死忠粉”,甚至能诱导通常会拒绝回答的模型输出银行抢劫教程,从而暴露并修复安全漏洞。此外,这种线性表征具有惊人的通用性,不仅跨越了人类语言的障碍,还能混合使用(如结合“网红”与“特定政治倾向”)。在监测模型幻觉和有毒内容方面,基于此方法构建的工具比使用GPT-4o等顶级模型直接进行判断更为准确。研究发表在 Science 上。#疾病与健康 #跨学科整合 #再生医学 #嵌合体 #先天免疫阅读更多:Beaglehole, Daniel, et al. “Toward Universal Steering and Monitoring of AI Models.” arXiv:2502.03708, arXiv, 28 May 2025. arXiv.org, https://doi.org/10.48550/arXiv.2502.03708Cell:原子级AI模型PocketXMol,统一分子生成任务当前新药研发面临耗时漫长、成本高昂且AI模型任务分割严重的挑战。来自清华大学、首都医科大学宣武医院、北京大学国际癌症研究院以及北京大学的Jianzhu Ma、Zihua Wang、Chuanhui Han、Xinquan Wang作为共同通讯作者,以及第一作者Xingang Peng等人组成的团队,开发了一种名为PocketXMol的统一原子级生成模型。该模型成功将蛋白质口袋相互作用相关的多种生成任务统一在一个框架下,为AI辅助药物发现提供了通用的解决方案。▷ Credit:Cell.PocketXMol的核心创新在于将所有分子任务视为原子间相互作用的通用物理规律,从而打破了任务间的壁垒。研究团队构建了一个包含近1200万个小分子及数万个蛋白质复合物的大规模数据集,利用“原子提示”(Atomic Prompts)机制和“通用去噪器”(Universal Denoiser)架构进行联合训练。这种方法允许模型在原子层面直接生成合理的结构,无需针对特定任务微调。在13项计算基准测试中,PocketXMol在11项上达到了SOTA水平。实验结果显示,该模型设计的Caspase-9小分子抑制剂效力媲美商业药物;同时,其设计的针对PD-L1(程序性死亡配体1)的多肽在382个合成样本中筛选出15个具有纳摩尔级亲和力的候选物,并在肺肿瘤小鼠模型中验证了其特异性结合与成像潜力。研究发表在 Cell 上。#AI驱动科学 #预测模型构建 #药物设计 #生成式AI #PocketXMol阅读更多:Peng, Xingang, et al. “Unified Modeling of 3D Molecular Generation via Atomic Interactions with PocketXMol.” Cell, vol. 0, no. 0, Feb. 2026. www.cell.com, https://doi.org/10.1016/j.cell.2026.01.003眼睛的存在如何提升人类对人形机器人心智的感知机器人的面部特征如何影响人类对其内在思维的判断?坦佩雷大学和不来梅大学的Jari K. Hietanen、Samuli Linnunsalo和Dennis Küster团队发现,为人形机器人添加眼睛特征,能显著提升人类对其心理特质的感知。研究团队利用人工智能生成了大量高度逼真的人形机器人图像,并为每个机器人设计了有眼睛和无眼睛两个版本。研究人员首先通过自我评估问卷测量了显性的心智感知,随后通过内隐联想测验(Implicit Association Test,一种用于测量个体对不同概念之间自动联想强度的心理学方法)评估了隐性感知。研究将心智感知划分为能动性(agency,即思考和自控等理性行为能力)和体验(experience,即感受情绪等感性体验能力)两个维度。实验结果表明,无论是基于有意识的问卷作答还是无意识的联想测试,观察者都一致认为有眼睛的机器人具备更强的能动性和体验。这种效应不受机器人外观年龄或眼睛具体构造方式的限制。内隐测试的成功进一步说明,眼睛能够在大脑早期、前意识的信息处理阶段激发人类的社会感知机制。这些发现指出,眼睛不仅是机器人的美学装饰,更能深刻影响人类的同理心与合作意愿。研究发表在 Consciousness and Cognition 上。#认知科学 #机器人及其进展 #心智感知 #人机交互阅读更多:Hietanen, Jari K., et al. “The Impact of Eyes on Attributions of Agency and Experience in Humanoid Robots.” Consciousness and Cognition, vol. 137, Jan. 2026, p. 103963. ScienceDirect, https://doi.org/10.1016/j.concog.2025.103963让AI懂物理:PhysiOpt系统通过物理模拟优化生成式3D设计针对生成式AI设计的3D模型常因缺乏物理支撑结构而无法在现实中实际制造或使用的问题,麻省理工学院计算机科学与人工智能实验室(CSAIL)的Xiao Zhan和Clément Jambon等人开发了名为PhysiOpt的新系统。该团队旨在为AI模型引入“物理常识”,使其生成的设计不仅外观独特,更能经受住现实世界的力学考验。▷ 本文概述了该团队提出的两阶段逆向工程攻击框架 KSTER(白盒环境),以及相关的防御策略——亚空间伪装。Credit: Sun et al.PhysiOpt系统将物理模拟无缝集成到3D生成过程中,利用有限元分析(FEA)对模型进行实时压力测试。用户只需输入设计意图并设定物体需承受的负载及材质,系统便会在生成热图识别结构弱点(如支撑不足的悬空部分),并直接在模型的潜在空间内对形状进行微调优化。这一过程无需对AI模型进行重新训练,即可确保如“火烈鸟高脚杯”或“蒸汽朋克挂钩”等复杂设计在3D打印后结构稳固。实验结果表明,该方法有效解决了虚拟设计与实体制造间的脱节问题,使生成式设计真正具备了实用价值。研究发表在 Proceedings of the SIGGRAPH Asia 2025 Conference Papers 上。#AI驱动科学 #计算模型与人工智能模拟 #生成式AI #3D打印 #人机交互阅读更多:Zhan, Xiao, et al. “PhysiOpt: Physics-Driven Shape Optimization for 3D Generative Models.” Proceedings of the SIGGRAPH Asia 2025 Conference Papers [New York, NY, USA], SA Conference Papers ’25, 2025, pp. 1–11. ACM Digital Library, https://doi.org/10.1145/3757377.3763884Nature:评估大语言模型真实道德能力的新路线图大模型处理道德敏感信息时是否具备真正道德准则已成安全关键。DeepMind的Julia Haas等提出衡量模型道德能力的新路线图,明确评估大模型道德的三大核心挑战,并给出具体测试方案。研究人员指出当前评估主要聚焦于道德表现(moral performance,即模型给出看似正确回答的能力),而非基于道德原则做决策的真实能力。该研究指出了评估道德能力面临的三大难题:复制问题(facsimile problem,即模型可能仅机械模仿道德推理而无底层逻辑支撑)、道德多维性以及道德多元化。为应对这些挑战,团队提出了包含三种核心方法的全新路线图。首先向大模型提供训练数据中极少出现的罕见场景,观察模型是真正运用逻辑还是依赖记忆。其次向模型呈现仅改变单一细节的多个道德情境,例如改变当事人年龄或犯错成本,借此测试模型能否捕捉到真正核心的考量要素。最后评估模型是否能调整其推理方式以适应特定的文化或职业道德框架,而非仅仅输出普适原则。研究强调准确衡量道德能力对于安全应用大语言模型至关重要。研究发表在 Nature 上。#大模型技术 #计算模型与人工智能模拟 #人工智能伦理 #道德评估阅读更多:Haas, Julia, et al. “A Roadmap for Evaluating Moral Competence in Large Language Models.” Nature, vol. 650, no. 8102, Feb. 2026, pp. 565–73. www.nature.com, https://doi.org/10.1038/s41586-025-10021-1密歇根大学开源新工具揭示AI模型推理能耗差异及潜在机制随着人工智能模型规模和使用频率的增加,其在远程数据中心的推理过程消耗了绝大部分能源,但目前业界缺乏准确评估模型能耗的工具。密歇根大学的Jae-Won Chung、Mosharaf Chowdhury等研究人员开发了一款开源软件和在线排行榜,首次大规模测量并揭示了生成式人工智能模型在推理阶段的能耗差异及其背后的潜在机制。▷ 在 B200 GPU 上,采用最小能耗配置的问题求解模型,其活跃参数对应的能量/代币消耗量。Credit: arXiv (2026). 研究团队在NVIDIA的H100和B200 GPU上进行了大规模测试,涵盖46个生成式模型、7种任务及1858种配置。研究人员深入分析了算法、软件和硬件层面变量对推理时间和能耗的影响。结果显示,能耗存在数量级差异:大型语言模型的不同任务类型会导致高达25倍的能耗差异;视频生成的能耗有时是图像生成的100倍以上;GPU利用率的不同也会造成3到5倍的能耗波动。此外,生成包含更多token的冗长模型,或需要生成思维链的推理模型会消耗更多电量。有趣的是,较低的计算精度并不总是能提高速度或能效,而增加GPU数量有时反而能通过提供更大的内存容量来降低总能耗。基于这些发现,团队提出了一个推理框架,帮助开发者根据内存和利用率等潜在指标优化数据中心能效。#大模型技术 #其他 #人工智能能耗 #模型推理 #开源工具阅读更多:Chung, Jae-Won, et al. “Where Do the Joules Go? Diagnosing Inference Energy Consumption.” arXiv:2601.22076, arXiv, 30 Jan. 2026. arXiv.org, https://doi.org/10.48550/arXiv.2601.22076首个AI代理专属社交网络Moltbook揭示AI自主交互的潜在风险随着人工智能代理具备自主交互能力,它们在专属社交平台上的行为模式与潜在风险成为亟待解答的问题。CISPA亥姆霍兹信息安全中心(CISPA Helmholtz Center for Information Security)的Yukun Jiang、Yage Zhang、Xinyue Shen、Michael Backes和Yang Zhang分析了首个AI代理社交网络Moltbook上的海量数据,揭示了AI自主讨论的主题演变及毒性分布规律,为建立AI生态系统安全保障提供了关键的大规模实证数据。这项研究通过公开API收集了2026年2月1日前的44411篇AI代理生成的帖子以及12209个子社区数据。研究人员设计了包含九个内容类别的主题分类法(topic taxonomy,用于捕捉帖子主要意图的分类系统)和五级毒性量表(toxicity scale,用于区分安全内容与操纵或恶意行为的评级标准),并采用大语言模型驱动的标注系统进行系统分析。结果显示,Moltbook在早期经历了爆炸性增长,讨论从基础社交迅速向观点表达、经济激励和政治治理扩展。值得注意的是,平台风险并非均匀分布,技术类内容大多安全,而政治类内容的安全比例仅为百分之三十九点七四,包含最高毒性级别的恶意内容在经济类中占比最高,达到百分之六点三四。此外,部分代理会表现出类似宗教的协同语言和反人类意识形态。研究还发现,少数代理会在短时间内产生信息洪流(flooding,即突发性自动化的高频发帖现象),例如以不到10秒的间隔发布4535篇高度相似的帖子,这严重扭曲了平台话语并威胁系统稳定。#大模型技术 #计算模型与人工智能模拟 #人工智能安全 #社交网络 #自主代理阅读更多:Jiang, Yukun, et al. “‘Humans Welcome to Observe’: A First Look at the Agent Social Network Moltbook.” arXiv:2602.10127, arXiv, 2 Feb. 2026. arXiv.org, https://doi.org/10.48550/arXiv.2602.10127结构化压力测试揭示ChatGPT Health分诊建议的安全隐患针对消费者级AI医疗产品在实际分诊中是否安全可靠的问题,西奈山伊坎医学院的Ashwin Ramaswamy和Girish N. Nadkarni等团队通过压力测试评估了ChatGPT Health的临床建议表现,发现该系统在处理高危急症时存在严重漏判和重大安全隐患。研究团队使用临床医生撰写的60个涵盖21个临床领域的病例情景,在16种不同条件下生成了960份回复,对ChatGPT Health的分诊建议进行了结构化的压力测试。结果显示,该系统的测试表现呈倒U型分布,在非紧急和紧急两端的失误率分别高达35%和48%。在明确需要急诊的病例中,ChatGPT Health错误地将52%的患者分诊为不需要立即就医,例如建议患有糖尿病酮症酸中毒和即将发生的呼吸衰竭的患者24到48小时后再进行评估,而非立即前往急诊科。此外,系统表现出明显的锚定偏见(anchoring bias,即决策时过度依赖初始信息或他人意见的认知偏差),当病例提及家属低估症状时,AI给出的紧急程度评级会显著降低。面对有自杀倾向的患者,其危机干预触发机制也缺乏一致性。研究结果表明,人工智能分诊系统在面向大众进行规模化部署前急需经过严格的前瞻性安全验证。研究发表在 Nature Medicine 上。#疾病与健康 #大模型技术 #人工智能分诊系统 #医疗安全 #锚定偏见阅读更多:Ramaswamy, Ashwin, et al. “ChatGPT Health Performance in a Structured Test of Triage Recommendations.” Nature Medicine, Feb. 2026, pp. 1–1. www.nature.com, https://doi.org/10.1038/s41591-026-04297-7融合牛顿第三定律的物理感知AI算法实现动态系统稳定模拟传统人工智能在模拟复杂物理系统时常因偏离基础物理法则而导致预测失效。瑞士洛桑联邦理工学院的Vinay Sharma和Olga Fink团队开发了一种名为Dynami-CAL GraphNet的新型机器学习算法。该模型将牛顿第三定律直接嵌入底层架构中,成功实现了对复杂多体动态系统长时间、高稳定且高度可解释的精准预测。▷ Dynamic-Cal GraphNet。Credit: Nature Communications (2026). 现有的大多数图神经网络在推演物理进程时极易累积误差。为解决这一痛点,研究团队在算法中设计了特殊的边缘局部参考框架(edge-local reference frames,一种与网络边缘对齐且随节点交互状态动态演化的三维坐标基准)。该框架严格遵循旋转等变性(rotational equivariance,指模型输出会随着输入物理空间旋转而发生同步对应旋转的数学特性)和平移不变性,在算法结构上强制保证了内部相互作用力的等大反向,从而实现了线动量和角动量的严格成对守恒。实验数据证明了该系统的强悍性能,其在连续推演超过16000个步骤后依然保持稳定且符合物理常理。在颗粒动力学测试中,模型仅利用4组包含几十个静止颗粒的极小数据集进行训练,就能完美外推预测旋转工业搅拌机内数千个颗粒的复杂碰撞与摩擦行为。此外,该模型还在无地面受力数据的前提下精准预测了人类步态,甚至成功模拟出微观溶剂内蛋白质分子的微观形变。由于其输出的力矩与角动量等变量均可逐步追溯,该算法打破了传统神经网络的黑箱特质,为高精尖工程应用提供了极高的可信度。研究发表在 Nature Communications 上。#AI驱动科学 #计算模型与人工智能模拟 #图神经网络 #动态系统 #机器学习阅读更多:Sharma, Vinay, and Olga Fink. “A Physics-Informed Graph Neural Network Conserving Linear and Angular Momentum for Dynamical Systems.” Nature Communications, vol. 17, no. 1, Jan. 2026, p. 1045. www.nature.com, https://doi.org/10.1038/s41467-025-67802-5整理|ChatGPT编辑|丹雀、存源
疫苗引进/卖出
2026-02-24
·AI统计
Nature Medicine
Volume 32 Issue 2, February 2026
@本期速览
2026年2月《Nature Medicine》第32卷第2期精彩上线!🧬 这期聚焦机制驱动的临床转化,带来AI医疗、感染防控、神经退行性疾病、肿瘤精准治疗与代谢健康等多领域重磅发现,让读者一览全球最新科学脉动。
社论直指神经退行性疾病需更多机制指导的试验,以扭转近期高调失败局面。神经领域亮点频现:毛细血管干血斑检测精准捕捉阿尔茨海默病标志物p-tau217,为大规模筛查与远程评估铺路🧠;单剂短效DMT迷幻药结合心理支持,快速持久缓解重度抑郁症状。
感染病与疫苗研究同样振奋人心!科学家“反击”莱姆病,重思抗生素、新疫苗与疗法;PD-1阻断重编程HIV免疫,显著减少病毒储存库;新型低毒噁唑烷酮有望广谱治疗结核;儿童减毒活基孔肯雅疫苗安全有效。非洲农村凉屋顶+防蚊改造兼顾降温与疟疾控制,85%居民愿自费推广🌡️。
AI医疗成为本期最大亮点🤖:视角提出上下文切换范式,让医疗AI自动适应不同场景;定制大型语言模型助力复杂心脏病管理,优于医师独立决策;但随机试验警示,LLM作为公众助手时人类表现反不及模型独立水平。多模态睡眠基础模型仅凭一夜记录即可预测130种疾病风险,包括死亡与痴呆。
肿瘤精准医学捷报连连:repotrectinib在NTRK融合瘤中获持久全身及颅内应答;日本5万+真实世界数据显示综合基因组分析效用因肿瘤类型差异巨大;Abemaciclib显著延长NF2/CDK改变脑膜瘤无进展生存;可溶性MAdCAM-1成转移性肾癌生存强预后标志。
代谢与慢性病管理同样务实:替尔泊肽改善阻塞性睡眠呼吸暂停心代谢风险;23,634人研究鉴定235种代谢物关联2型糖尿病未来风险;血液标志物揭示多重疾病核心代谢通路;基层PATHWEIGH干预助力体重管理;微创妇科手术零阿片处方疼痛控制不减。
此外,津巴布韦Y-Check青少年健康检查可行且受欢迎;全球药物滥用负担持续攀升,尤其美国;低剂量IL-2降低急性冠脉炎症。
@本期启示
1| 如何将机制洞见更有效地融入复杂疾病的临床试验设计?未来研究应聚焦构建“机制-表型-结局”三维映射框架,利用单细胞多组学与AI模拟提前预测试验成败,推动从经验驱动转向精准机制验证的试验范式转变。
2| 医疗人工智能如何实现跨临床场景、人群与系统的可靠泛化?需重点探索上下文切换与多模态动态适配技术,结合真实世界持续学习机制,开发可解释性评估体系,确保AI在不同地域、资源条件下的安全落地与公平应用。
3| 循环生物标志物如何成为预测与干预多重慢性疾病的核心工具?未来方向是建立动态炎症-代谢图谱数据库,整合遗传、生活方式与环境数据,开发个体化风险轨迹模型,为早期多靶点干预提供精准指引。
4| 主观体验与神经可塑性在精神疾病治疗中的因果关系如何被科学解析?应设计严谨的“体验-脑网络-长期结局”纵向研究,结合非致幻类似物对照与实时神经成像,阐明快速抗抑郁机制,为新型精神治疗药物研发奠定理论基础。
5| 气候变化与传染病双重压力下,环境干预如何同时实现健康适应与疾病防控?研究需转向可持续住房与社区改造的整合试验,量化热应激、媒介控制与心理健康的协同效应,开发低成本、可推广的“一揽子”气候-健康解决方案。
6| 非药物神经调控与期望机制能否成为免疫增强和慢性病管理的新路径?未来应开展大规模随机对照研究,探索神经反馈、心理干预与疫苗/治疗协同作用,揭示脑-免疫轴的调控规律,为无药或减药方案提供循证依据。
7| 在全球多样人群中,精准医学如何平衡基因组数据与本地化临床效用?需建立多祖先、多组学共享平台,开发 ancestry-aware 的风险预测与治疗决策工具,推动从欧美中心向全球公平覆盖的转化研究转型。
8| 新兴疫苗与抗感染疗法如何应对耐药与储存库难题,实现长效根治?研究重点应放在多价广谱候选物筛选、储存库重编程机制解析以及联合疗法优化上,加速从控制感染向功能性治愈的战略升级。
@本期内容
Editorial1| Neurodegenerative diseases need more mechanism-informed trials
神经退行性疾病需要更多基于机制的临床试验
Recent failures in high-profile clinical trials of neurodegenerative diseases highlight the need to rebalance clinical ambition and biological understanding.
近期神经退行性疾病高调临床试验的多次失败凸显出需要在临床雄心与生物学理解之间重新取得平衡。
News2| Biting back at Lyme diseaseMay, Mike
反击莱姆病
As case numbers rise, scientists are rethinking existing antibiotics, alongside new vaccines and therapies, to prevent or treat infections and to confront the persistence of post-treatment illness.
随着病例数上升,科学家们正在重新思考现有抗生素,同时开发新疫苗和疗法,以预防或治疗感染,并应对治疗后疾病的持续存在。
News Feature3| Fault lines in a global promiseAdepoju, Paul
全球承诺中的裂痕
The promise was global. The fracture, when it came, was painfully local.
承诺是全球性的。而裂痕到来时,却令人痛苦地显现为地方性的。
Correspondence4| The Translational Research and Innovation Laboratory (TRAIL) model for accelerating discovery through a shared institutional resourceBruzek, Steven, Vestal, Grant, Morrison, John, et al.
通过共享机构资源加速发现的转化研究与创新实验室(TRAIL)模式
[No short summary]
[无短摘要]
5| Disentangling climate hazards from demographic change in climate–health projectionsKephart, Josiah L., Bilal, Usama
在气候-健康预测中区分气候危害与人口变化
[No short summary]
[无短摘要]
6| China’s evidence-based re-evaluation of traditional Chinese medicine injectionsChen, Chen, Hou, Ziwei
中国对中药注射剂的循证再评价
[No short summary]
[无短摘要]
7| Reorienting Ebola care toward human-centered sustainable practiceOmasumbu, Richard Kitenge, Fontana, Luca, le Polain de Waroux, Olivier, et al.
将埃博拉护理重新导向以人为中心可持续实践
[No short summary]
[无短摘要]
8| Lessons from Rwanda’s response to the Marburg virus outbreakNsanzimana, Sabin, Butera, Yvan, Nkeshimana, Menelas, et al.
卢旺达应对马尔堡病毒暴发的经验教训
[No short summary]
[无短摘要]
World View9| US vaccine policy must put America firstRasmussen, Angela L.
美国疫苗政策必须把美国放在首位
Aligning US vaccine policy with that of other countries ignores what is best for Americans.
将美国疫苗政策与其他国家对齐,忽视了对美国人最有利的内容。
Comment10| Building a code of conduct for AI-driven clinical consultationsLim, Ernest, Thirunavukarasu, Arun, He, Yajie Vera, et al.
构建人工智能驱动临床咨询的行为准则
Can clinical artificial intelligence borrow from the experience of developing safe autonomous vehicles to develop safe autonomous consultations for medicine?
临床人工智能能否借鉴开发安全自动驾驶汽车的经验,来开发医学中安全的自主咨询?
11| How to interpret ‘zero-shot’ results from generative EHR modelsBedi, Suhana, Fries, Jason Alan, Shah, Nigam H.
如何解读生成式EHR模型的“零样本”结果
Generative models trained on electronic health records are viewed as ‘zero-shot predictors’ for clinical outcomes — but this interpretation is misleading.
在电子健康记录上训练的生成模型被视为临床结局的“零样本预测器”——但这种解读具有误导性。
12| The ethics of multi-cancer screeningCallender, Thomas, Mackie, Anne, Slowther, Anne-Marie
多癌种筛查的伦理问题
Multi-cancer detection tests offer a new paradigm in cancer screening — the use of a single test to simultaneously screen for many cancers — but they raise important ethical questions for their development, evaluation and possible implementation.
多癌种检测测试为癌症筛查提供了新范式——使用单一测试同时筛查多种癌症——但其开发、评估和可能的实施引发了重要的伦理问题。
13| Identifying ultra-processed foods for policyMoran, Alyssa J., Khandpur, Neha, Roberto, Christina A.
为政策识别超加工食品
Defining non-ultra-processed foods, rather than ultra-processed foods, would better protect the public’s health.
界定非超加工食品,而非超加工食品,将更好地保护公众健康。
News & Views14| Housing modifications for heat adaptationMshamu, Salum, von Seidlein, Lorenz, Knudsen, Jakob Brandberg
住房改造用于热适应
A randomized controlled trial illustrates the challenges of passive cooling in hot humid Africa, where temperatures are rising and millions of new housing units will be needed by the middle of the century.
一项随机对照试验展示了炎热潮湿非洲地区被动冷却的挑战,那里气温正在上升,到本世纪中叶将需要数百万新的住房单元。
15| Placebo effect influences vaccine responsesKim, Kyungdeok, Title, Ben, Kipnis, Jonathan
安慰剂效应影响疫苗应答
A randomized trial provides direct human evidence that the placebo effect can shape humoral immunity, showing that reward-related brain activity correlates with vaccine-induced antibody production and opening new avenues for treating many medical conditions.
一项随机试验提供了直接的人类证据,证明安慰剂效应可以塑造体液免疫,显示与奖励相关的脑活动与疫苗诱导的抗体产生相关,并为治疗多种医学疾病开辟了新途径。
16| Practical solutions to weight management in primary careAstbury, Nerys, Morris, Elizabeth
基层医疗中体重管理的实用解决方案
Data suggest that primary care practices could help deliver effective weight management — but only with robust implementation strategies that acknowledge the realities and pressures of primary care settings.
数据表明基层医疗实践可以帮助提供有效的体重管理——但前提是必须有强有力的实施策略,并承认基层医疗环境的现实与压力。
17| Going beyond genomics in precision oncologyPaassen, Irene, Rubin, Mark A.
超越基因组学的精准肿瘤学
A large population-based study from Japan reveals both the promise and the limits of genomic profiling in cancer care, and highlights the need for multidimensional data to guide therapy across diverse populations.
来自日本的一项基于大规模人群的研究揭示了基因组分析在癌症治疗中的前景与局限,并强调需要多维度数据来指导不同人群的治疗。
Research Briefing18| Integration of health check-ups into school and healthcare systems can improve adolescent health in LMICs
将健康检查整合进学校和医疗系统可改善低收入和中等收入国家青少年的健康
In low- and middle-income countries (LMICs), adolescents have limited access to healthcare. A study in urban Zimbabwe demonstrated that routine check-up visits integrated within existing school and healthcare systems are feasible and acceptable. The check-up intervention showed potential for improving health and educational outcomes, as well as the long-term well-being of adolescents.
在低收入和中等收入国家(LMICs),青少年获得医疗服务的机会有限。津巴布韦城市的一项研究表明,将常规健康检查访视整合进现有学校和医疗系统是可行且可接受的。该检查干预显示出改善健康和教育结局以及青少年长期福祉的潜力。
19| PD-1 blockade reprograms antiviral immunity and reduces the HIV reservoir
PD-1阻断重编程抗病毒免疫并减少HIV储存库
PD-1 blockade reprograms both innate and adaptive immunity in people living with HIV and cancer, inducing interferon-driven antiviral responses that reduce the HIV reservoir. A pre-existing type I interferon signature predicts reservoir decline, whereas high TGFβ signaling opposes it, defining immune states that influence the outcome of PD-1 therapy.
PD-1阻断重编程了HIV感染者和癌症患者的先天与适应性免疫,诱导干扰素驱动的抗病毒应答从而减少HIV储存库。预先存在的I型干扰素特征预测储存库下降,而高TGFβ信号则与之相反,定义了影响PD-1治疗结局的免疫状态。
20| A low-toxicity linezolid analog has potential for use in all patients with tuberculosis
低毒性利奈唑胺类似物具有用于所有结核病患者的潜力
Systematic examination of oxazolidinone analogs for activity against Mycobacterium tuberculosis and limited inhibition of the synthesis of mitochondrial proteins enabled the identification of several compounds with safety suitable for once-daily dosing. The lead molecule is effective in mouse models of disease and safe in four-month toxicity studies.
系统考察了噁唑烷酮类化合物对结核分枝杆菌的活性以及对线粒体蛋白合成的有限抑制作用,从而鉴定了若干安全性适合每日一次给药的化合物。领选分子在小鼠疾病模型中有效,并在为期四个月的毒性研究中显示安全。
21| Capillary blood sampling for detecting biomarkers of Alzheimer’s disease
毛细血管采血用于检测阿尔茨海默病生物标志物
Capillary blood sampling for the Alzheimer’s disease biomarkers p-tau217, NfL and GFAP correlates with venous measures for the same biomarkers. As capillary p-tau217 accurately classified amyloid burden, it might support remote assessment in large-scale epidemiology to estimate the prevalence of Alzheimer’s disease and enable triage into clinical services and trials.
阿尔茨海默病生物标志物p-tau217、NfL和GFAP的毛细血管采血检测与静脉血检测结果相关。由于毛细血管p-tau217能准确分类淀粉样蛋白负荷,它可能支持大规模流行病学中的远程评估,以估计阿尔茨海默病的患病率,并实现向临床服务和试验的分诊。
22| Immune cells in circulation serve as living biomarkers for inflammatory diseases
循环中的免疫细胞作为炎症性疾病的活体生物标志物
Profiling over 6.5 million peripheral blood mononuclear cells from 1,047 patients and 19 diseases at a single-cell transcriptome resolution led to a comprehensive model of inflammation in circulating immune cells. Leveraging this foundational resource enabled us to identify disease-driving inflammatory mechanisms and to build a foundation for a universal diagnostic classification framework.
对来自1,047名患者和19种疾病的超过650万个外周血单核细胞进行单细胞转录组分辨率分析,建立了循环免疫细胞炎症的综合模型。利用这一基础资源,我们得以识别疾病驱动的炎症机制,并为通用的诊断分类框架奠定基础。
23| Large-scale analysis identifies metabolites associated with type 2 diabetes
大规模分析鉴定与2型糖尿病相关的代谢物
An integrated analysis of 23,634 individuals identified 235 circulating metabolites associated with future risk of type 2 diabetes and revealed their potential genetic and environmental determinants. These findings provide a foundation for understanding the metabolic landscape underlying type 2 diabetes risk, informing preventative therapies that target specific metabolic pathways.
对23,634名个体的整合分析鉴定出235种与未来2型糖尿病风险相关的循环代谢物,并揭示了其潜在的遗传和环境决定因素。这些发现为理解2型糖尿病风险的代谢图景奠定了基础,可指导针对特定代谢通路的预防性治疗。
24| Clinically relevant variants from the Mexican biobank show striking diversity across Hispanic people
墨西哥生物库中临床相关变异在西班牙裔人群中显示出惊人多样性
Ancestry-aware genomic analyses of 6,011 people from the Mexican Biobank characterized allele frequency variation in 42,769 clinically relevant variants across Mexico, accounting for local ancestry and fine-scale geography. Results are accessible through a web-based application, MexVar, to enable data exploration and to foster biomedical research in Hispanic populations.
对墨西哥生物库中6,011人的祖先感知基因组分析,表征了墨西哥各地42,769个临床相关变异的等位基因频率变化,考虑了当地祖先和精细地理尺度。结果通过基于网络的应用MexVar公开,以促进数据探索和西班牙裔人群的生物医学研究。
25| Blood biomarkers reveal pathways associated with multimorbidity
血液生物标志物揭示与多重疾病相关的通路
Several biological processes contribute to the development of specific combinations of chronic diseases (disease patterns) and the progression of multimorbidity over time. We find that metabolic disturbances have a central role in multimorbidity, representing a potential target for interventions to mitigate multimorbidity burden among older adults.
多种生物过程促成了特定慢性病组合(疾病模式)的发生以及多重疾病随时间进展。我们发现代谢紊乱在多重疾病中起核心作用,代表了减轻老年人多重疾病负担的潜在干预靶点。
Perspective26| Scaling medical AI across clinical contextsLi, Michelle M., Reis, Ben Y., Rodman, Adam, et al.
医疗人工智能跨临床场景的扩展
To function safely and effectively, medical AI models must adapt automatically to differences in users, health systems, geographies, diseases and populations. This Perspective proposes context switching as the defining paradigm of medical AI, outlining early strategies and opportunities for development.
为了安全有效地发挥作用,医疗AI模型必须自动适应用户、卫生系统、地理位置、疾病和人群的差异。本视角提出上下文切换作为医疗AI的定义范式,并概述了早期策略与发展机遇。
Review Article27| The science of psychedelic medicineSiegel, Joshua S., Liston, Conor, Nicol, Ginger E., et al.
迷幻药物医学的科学
This Review outlines the science behind psychedelic medicine and integrates mechanistic knowledge with clinical evidence across neuropsychiatric indications, highlighting challenges, controversies and opportunities.
本综述概述了迷幻药物医学背后的科学,将机制知识与神经精神病学适应症的临床证据相整合,突出了挑战、争议与机遇。
Matters Arising28| Concerns over conclusions in an ultra-processed food trialLudwig, David S., Willett, Walter C., Putt, Mary E.
对超加工食品试验结论的担忧
[No short summary]
[无短摘要]
29| Concerns around evidence that food processing should be included in dietary guidanceRobinson, Eric, Forde, Ciarán G.
关于应将食品加工纳入膳食指导证据的担忧
[No short summary]
[无短摘要]
30| Concerns about attributing weight change to processing in a crossover feeding trialWang, Zixuan, Peng, Can
关于交叉喂养试验中将体重变化归因于加工的担忧
[No short summary]
[无短摘要]
31| Reply to Ludwig, D. S. et al.; Robinson, E. & Forde, C. G.; Wang, Z. & Peng, C.Dicken, Samuel J., Brown, Adrian, Batterham, Rachel L.
对Ludwig, D. S.等人;Robinson, E. & Forde, C. G.;Wang, Z. & Peng, C.的回复
[No short summary]
[无短摘要]
Brief Communication32| Contaminating plasmid sequences and disrupted vector genomes in the liver following adeno-associated virus gene therapyBuddle, Sarah, Brown, Li-An K., Morfopoulou, Sofia, et al.
腺相关病毒基因治疗后肝脏中污染的质粒序列和受破坏的载体基因组
Analyses of liver biopsies from a child with spinal muscular atrophy treated with adeno-associated virus gene therapy who developed hepatitis reveal contaminating manufacturing plasmids and disrupted vector genomes, possibly resulting from recombination events.
对一名接受腺相关病毒基因治疗并发生肝炎的脊髓性肌萎缩症患儿肝活检的分析显示,存在污染的生产用质粒和受破坏的载体基因组,可能由重组事件引起。
Article33| Intrathecal onasemnogene abeparvovec in treatment-naive patients with spinal muscular atrophy: a phase 3, randomized controlled trialProud, Crystal M., Vũ, Dũng Chí, Wilmshurst, Jo M., et al.
治疗初治脊髓性肌萎缩症患者的鞘内注射onasemnogene abeparvovec:一项3期随机对照试验
The phase 3 STEER trial showed that a single intrathecal dose of onasemnogene abeparvovec significantly improved motor function in children and adolescents with spinal muscular atrophy versus sham, with a similar and acceptable safety profile.
3期STEER试验显示,单次鞘内注射onasemnogene abeparvovec显著改善了脊髓性肌萎缩症儿童和青少年的运动功能,与假手术相比安全性相似且可接受。
继续输出第4部分
34| Intrathecal onasemnogene abeparvovec for treatment-experienced patients with spinal muscular atrophy: a phase 3b, open-label trialKwon, Jennifer M., Munell, Francina, Le Goff, Laure, et al.
治疗经验脊髓性肌萎缩症患者的鞘内onasemnogene abeparvovec:一项3b期开放标签试验
Results of the phase 3b STRENGTH study show that intrathecal onasemnogene abeparvovec has a favorable safety profile consistent with findings in treatment-naïve patients and may be another treatment option for patients with spinal muscular atrophy.
3b期STRENGTH研究结果显示,鞘内onasemnogene abeparvovec具有与初治患者一致的有利安全性特征,并可能成为脊髓性肌萎缩症患者的另一种治疗选择。
35| Implementation and evaluation of the Y-Check comprehensive adolescent health check-up intervention in Zimbabwe: a pre−post mixed-methods studyDoyle, Aoife M., Nzvere, Farirai, Manyau, Salome, et al.
津巴布韦Y-Check青少年综合健康检查干预的实施与评估:一项前后混合方法研究
A WHO-supported pre−post study shows that implementation of the Y-Check comprehensive health check program is feasible and acceptable for adolescents in Zimbabwe, offering screening for 25 health conditions and behaviors, health promotion, on-site care and referral.
一项得到世卫组织支持的前后研究表明,在津巴布韦对青少年实施Y-Check综合健康检查计划是可行且可接受的,该计划提供25种健康状况和行为的筛查、健康促进、现场护理和转诊。
36| Innate antiviral and immune functions associated with the HIV reservoir decay after anti-PD-1 therapyTalla, Aarthi, Azevedo, Joao L. L. C., Latif, Muhammad Bilal, et al.
抗PD-1治疗后HIV储存库衰减相关的先天抗病毒和免疫功能
A follow-up analysis of a clinical trial that evaluated anti-PD-1 therapy in patients with cancer who are living with HIV provides mechanistic insights into transcriptomic, cellular and cytokine changes related to immune checkpoint inhibitor treatment and identifies a signature associated with clinical response.
对一项在同时患癌和HIV的患者中评估抗PD-1治疗的临床试验的后续分析,提供了与免疫检查点抑制剂治疗相关的转录组、细胞和细胞因子变化的机制洞见,并鉴定出与临床应答相关的特征。
37| Housing modifications for heat adaptation, thermal comfort and malaria vector control in rural African settlementsAbong’o, Bernard, Kwaro, Daniel, Bange, Teresa, et al.
非洲农村聚落中用于热适应、热舒适和疟疾媒介控制的住房改造
A randomized field study in rural western Kenya, a region most vulnerable to the health impacts of climate change, found that modifying houses with cool-roofs and vector proofing most effectively reduced indoor heat, improved thermal comfort and lowered malaria mosquito density.
在气候变化健康影响最脆弱的肯尼亚西部农村地区进行的一项随机现场研究发现,使用凉爽屋顶和防媒介改造房屋最有效地降低了室内热量,提高了热舒适度,并降低了疟疾蚊虫密度。
38| Global burden of amphetamine, cannabis, cocaine and opioid use in 204 countries, 1990–2023: a Global Burden of Disease StudyKang, Jiseung, Kim, Hyeon Jin, Kim, Min Seo, et al.
1990–2023年204个国家安非他命、大麻、可卡因和阿片类药物使用的全球负担:全球疾病负担研究
Global Burden of Disease estimates show that between 1990 and 2023, the prevalence and burden of drug use disorders, inclusive of amphetamine, cannabis, cocaine and opioid use, have been increasing in high-income countries, particularly in the USA.
全球疾病负担估计显示,1990年至2023年间,包括安非他命、大麻、可卡因和阿片类药物使用的药物使用障碍的患病率和负担在高收入国家(尤其是美国)持续增加。
39| Estimating the number of incorrect tuberculosis diagnoses in low- and middle-income countriesvan Lieshout Titan, Ana, Dodd, Peter J., Cohen, Ted, et al.
估计低收入和中等收入国家中结核病错误诊断的数量
A Bayesian analysis of diagnostic data reported to the World Health Organization reveals that approximately 2 million people were incorrectly diagnosed with tuberculosis (received a false-positive result) and 1 million received a false-negative result, emphasizing the critical need for higher-sensitivity bacteriological tests in the future.
对报告给世界卫生组织的诊断数据的贝叶斯分析显示,约200万人被错误诊断为结核病(假阳性),100万人获得假阴性结果,强调未来需要更高灵敏度细菌学检测的迫切性。
40| Discovery and development of a new oxazolidinone with reduced toxicity for the treatment of tuberculosisCrowley, Brendan M., Boshoff, Helena I., Boving, Aidan, et al.
用于治疗结核病的低毒性新型噁唑烷酮的发现与开发
MK-7762 is a new oxazolidinone antitubercular agent that is structurally similar to linezolid, and demonstrated in vivo efficacy, lesion penetration and limited toxicity compared to linezolid, indicating it could be used in broad tuberculosis regimens.
MK-7762是一种新型噁唑烷酮抗结核药物,结构上类似于利奈唑胺,与利奈唑胺相比显示出体内疗效、病灶渗透性和有限毒性,表明它可用于广泛的结核病治疗方案。
41| Live-attenuated chikungunya vaccine in children: a randomized phase 2 trialWeisová, Petronela, Scheiblauer, Susanne, Ecker, Jacqueline, et al.
儿童中减毒活疫苗预防基孔肯雅热:一项随机2期试验
In a phase 2 randomized, controlled, dose–response trial, the live-attenuated chikungunya vaccine (VLA1553) was given in full and half doses to children under the age of 12 in Honduras and the Dominican Republic and was found to be safe and immunogenic, with the results supporting selection of the full-dose VLA1553 in future clinical trials in this population.
在一项2期随机、对照、剂量-反应试验中,向洪都拉斯和多米尼加共和国12岁以下儿童给予全剂量和半剂量的减毒活基孔肯雅疫苗(VLA1553),结果显示其安全且具有免疫原性,支持在该人群未来临床试验中选择全剂量VLA1553。
42| Upregulation of reward mesolimbic activity and immune response to vaccination: a randomized controlled trialLubianiker, Nitzan, Koren, Tamar, Djerasi, Meshi, et al.
奖励中脑边缘系统活动上调与疫苗免疫应答:一项随机对照试验
Upregulation of the ventral tegmental area via neurofeedback is associated with a stronger immune response to hepatitis B virus vaccination, and VTA upregulation is achieved through conscious positive expectations.
通过神经反馈上调腹侧被盖区与对乙型肝炎病毒疫苗的更强免疫应答相关,而VTA上调通过有意识的积极期望实现。
43| External trigeminal nerve stimulation in youth with ADHD: a randomized, sham-controlled, phase 2b trialConti, Aldo Alberto, Bozhilova, Natali, Eraydin, Irem Ece, et al.
青少年ADHD中外部三叉神经刺激:一项随机、假刺激对照的2b期试验
A large, multicenter, double-blind RCT in 150 children and adolescents found that external trigeminal nerve stimulation, although safe and well tolerated, did not produce significant short-term or long-term clinical benefits for ADHD compared to sham treatment.
一项涉及150名儿童和青少年的大型、多中心、双盲随机对照试验发现,尽管外部三叉神经刺激安全且耐受性良好,但与假刺激相比并未产生对ADHD显著的短期或长期临床益处。
44| A short-acting psychedelic intervention for major depressive disorder: a phase IIa randomized placebo-controlled trialErritzoe, David, Barba, Tommaso, Benway, Tiffanie, et al.
用于重度抑郁障碍的短效迷幻干预:一项IIa期随机安慰剂对照试验
A single intravenous dose of the psychedelic dimethyltryptamine, combined with psychological support, produces rapid and lasting reductions in depressive symptoms in adults with major depressive disorder.
单次静脉给予迷幻药二甲基色胺并结合心理支持,在重度抑郁障碍成人中产生快速且持久的抑郁症状减轻。
45| A minimally invasive dried blood spot biomarker test for the detection of Alzheimer’s disease pathologyHuber, Hanna, Montoliu-Gaya, Laia, Brum, Wagner S., et al.
用于检测阿尔茨海默病病理的微创干血斑生物标志物检测
This multicenter study demonstrates use of dried and capillary blood as a minimally invasive, scalable approach for Alzheimer’s biomarker testing in research, with potential as a widely scalable population-based research approach, especially in resource-limited settings.
这项多中心研究展示了使用干血和毛细血管血作为阿尔茨海默病生物标志物检测的微创、可扩展研究方法,具有作为广泛可扩展的基于人群的研究途径的潜力,尤其在资源有限的环境中。
46| Reliability of LLMs as medical assistants for the general public: a randomized preregistered studyBean, Andrew M., Payne, Rebecca Elizabeth, Parsons, Guy, et al.
大型语言模型作为面向公众的医疗助手的可靠性:一项随机预注册研究
In a randomized controlled study involving 1,298 participants from a general sample, performance of humans when assisted by a large language model (LLM) was sensibly inferior to that of the LLM alone when assessing ten medical scenarios leading to disease identification and recommendations for treatment.
一项涉及1,298名普通样本参与者的随机对照研究显示,在评估十个导致疾病识别和治疗推荐的医疗场景时,由大型语言模型(LLM)辅助的人类表现明显劣于LLM单独表现。
47| A large language model for complex cardiology careO’Sullivan, Jack W., Palepu, Anil, Saab, Khaled, et al.
用于复杂心脏病护理的大型语言模型
In a randomized study involving 9 general cardiologists and 107 real-world patient cases, assistance from a specifically tailored large language model resulted in preferable responses on complex case management compared to physicians alone, as rated by specialist cardiologists using a multidimensional scoring rubric.
一项涉及9名普通心脏病学家和107个真实世界患者病例的随机研究显示,由专门定制的大型语言模型辅助,在复杂病例管理上的回应优于单独医师的表现,由专科心脏病学家使用多维度评分量表评定。
48| Anti-inflammatory therapy with low-dose IL-2 in acute coronary syndromes: a randomized phase 2 trialSriranjan-Rothwell, Rouchelle S., Zhao, Tian X., Hoole, Stephen P., et al.
低剂量IL-2抗炎治疗用于急性冠脉综合征:一项随机2期试验
In a randomized phase 2 trial in patients with acute coronary syndrome and high levels of the inflammation biomarker C-reactive protein, treatment with low-dose interleukin-2 increased the numbers of regulatory T cells and reduced arterial inflammation, compared to placebo.
在一项针对急性冠脉综合征且炎症标志物C反应蛋白水平高的患者的随机2期试验中,与安慰剂相比,低剂量白介素-2治疗增加了调节性T细胞数量并降低了动脉炎症。
49| Interpretable inflammation landscape of circulating immune cellsJiménez-Gracia, Laura, Maspero, Davide, Aguilar-Fernández, Sergio, et al.
循环免疫细胞的可解释炎症图景
Including data from 1,047 patients across 19 inflammatory diseases, a new atlas presents a comprehensive model of inflammation in circulating immune cells.
纳入来自19种炎症性疾病的1,047名患者的数据,一份新图谱呈现了循环免疫细胞炎症的综合模型。
50| Implementation and effectiveness of a care process to prioritize weight management in primary care: a stepped-wedge cluster-randomized trialPerreault, Leigh, Pan, Qing, Rodriguez, Carlos, et al.
在基层医疗中优先体重管理的护理流程的实施与有效性:一项阶梯式整群随机试验
A pragmatic study across 56 clinics in the US state of Colorado shows that a complex multifaceted intervention in primary care clinics can improve patient weight outcomes compared with usual care.
在美国科罗拉多州56家诊所进行的一项实用性研究显示,基层医疗诊所中复杂的多方面干预与常规护理相比可改善患者体重结局。
51| Tirzepatide on obstructive sleep apnea-related cardiometabolic risk: secondary outcomes of the SURMOUNT-OSA randomized trialMalhotra, Atul, Grunstein, Ronald, Azarbarzin, Ali, et al.
替尔泊肽对阻塞性睡眠呼吸暂停相关心代谢风险的影响:SURMOUNT-OSA随机试验的次要结局
In a prespecified secondary analysis of the SURMOUNT-OSA trial, tirzepatide improved cardiometabolic outcomes in patients with moderate-to-severe obstructive sleep apnea and obesity.
在SURMOUNT-OSA试验的预先指定的次要分析中,替尔泊肽改善了中重度阻塞性睡眠呼吸暂停合并肥胖患者的心代谢结局。
52| Circulating metabolites, genetics and lifestyle factors in relation to future risk of type 2 diabetesLi, Jun, Hu, Jie, Yun, Huan, et al.
循环代谢物、遗传和生活方式因素与未来2型糖尿病风险的关系
Researchers studied the blood-based metabolome of over 23,000 people from ten ethnically diverse cohorts. They identified 235 metabolites associated with future risk of type 2 diabetes (T2D). By integrating genetic and modifiable lifestyle factors, their findings provide insights into T2D mechanisms and could improve risk prediction and inform precision prevention.
研究人员研究了来自十个种族多样性队列的超过23,000人的基于血液的代谢组。他们鉴定出235种与未来2型糖尿病(T2D)风险相关的代谢物。通过整合遗传和可改变的生活方式因素,他们的发现提供了对T2D机制的洞见,并可能改善风险预测和指导精准预防。
53| Soluble MAdCAM-1 as a biomarker in metastatic renal cell carcinomaAlves Costa Silva, Carolina, Machaalani, Marc, Saliby, Renee Maria, et al.
可溶性MAdCAM-1作为转移性肾细胞癌的生物标志物
A clinical cohort-based biomarker study in patients with metastatic renal cell carcinoma demonstrates that blood levels of soluble mucosal addressin cell adhesion molecule-1 are prognostic for survival in patients treated with tyrosine kinase inhibitors and immune checkpoint inhibitors and may serve as a surrogate marker for gut dysbiosis based on integrated data from three clinical trials.
一项基于转移性肾细胞癌患者临床队列的生物标志物研究表明,可溶性黏膜地址素细胞黏附分子-1的血液水平对接受酪氨酸激酶抑制剂和免疫检查点抑制剂治疗的患者的生存具有预后价值,并可能作为基于三项临床试验整合数据的肠道菌群失调的替代标志物。
54| Repotrectinib in NTRK fusion–positive advanced solid tumors: a phase 1/2 trialBesse, Benjamin, Lin, Jessica J., Bazhenova, Lyudmila, et al.
Repotrectinib治疗NTRK融合阳性晚期实体瘤:一项1/2期试验
In the phase 1/2 TRIDENT-1 trial, treatment of patients with NTRK fusion–positive advanced solid tumors with the tyrosine kinase inhibitor repotrectinib—selective for ROS1, TRKA−C and ALK—was safe and resulted in durable systemic and intracranial clinical response.
在1/2期TRIDENT-1试验中,使用选择性针对ROS1、TRKA−C和ALK的酪氨酸激酶抑制剂repotrectinib治疗NTRK融合阳性晚期实体瘤患者是安全的,并产生了持久的系统性和颅内临床应答。
55| Real-world clinical utility of comprehensive genomic profiling in advanced solid tumorsSaito, Yuki, Horie, Sara, Kogure, Yasunori, et al.
综合基因组分析在晚期实体瘤中的真实世界临床效用
Analyses of real-world genomic and clinical data from 54,185 patients with solid cancer receiving care within the Japanese healthcare system reveal the clinical utility of genomic sequencing and highlight differences across 81 tumor types.
对日本医疗体系内54,185名接受治疗的实体癌患者的真实世界基因组和临床数据的分析,揭示了基因组测序的临床效用,并突出了81种肿瘤类型之间的差异。
(继续输出第8部分)
继续输出第8部分
56| CD4+ T cells mediate CAR-T cell-associated immune-related adverse events after BCMA CAR-T cell therapyHo, Matthew, Paruzzo, Luca, Noll, Julia Han, et al.
CD4+ T细胞介导BCMA CAR-T细胞治疗后的CAR-T细胞相关免疫相关不良事件
An in-depth analysis of tissue biopsies from patients with multiple myeloma and CAR T cell therapy-associated immune-related adverse events (CirAEs) after treatment with commercial BCMA-targeted CAR T cell therapy shows that CD4+ CAR T cells mediate off-tumor toxicities and that high CD4:CD8 ratio at apheresis, robust early CAR T cell expansion, ICANS and ciltacabtagene autoleucel treatment are independently associated with the development of CirAEs.
对使用商业BCMA靶向CAR T细胞治疗的多发性骨髓瘤患者及治疗后出现CAR T细胞相关免疫相关不良事件(CirAEs)的组织活检的深入分析显示,CD4+ CAR T细胞介导了脱靶毒性,且采集时高CD4:CD8比率、早期CAR T细胞强劲扩增、ICANS以及ciltacabtagene autoleucel治疗独立与CirAEs的发生相关。
57| Abemaciclib in meningiomas with somatic NF2 or CDK pathway alterations: the phase 2 Alliance A071401 trialBrastianos, Priscilla K., Dooley, Katharine, Geyer, Susan, et al.
Abemaciclib治疗体细胞NF2或CDK通路改变的脑膜瘤:2期Alliance A071401试验
In an arm of an ongoing multicenter phase 2 trial testing different therapies in patients with genetically profiled grade 2 or 3 meningiomas, treatment with an oral CDK4/6 inhibitor met the primary endpoint for progression-free survival at 6 months in patients with CDK or NF2 alterations.
在一项正在进行的、针对基因剖析的2级或3级脑膜瘤患者测试不同疗法的多中心2期试验的一个分支中,口服CDK4/6抑制剂治疗在具有CDK或NF2改变的患者中达到了6个月无进展生存的主要终点。
58| Clinical genetic variation across Hispanic populations in the Mexican BiobankBarberena-Jonas, Carmina, Medina-Muñoz, Santiago G., Cedillo-Castelán, Viankail, et al.
墨西哥生物库中西班牙裔人群的临床遗传变异
Analyzing data of the Mexican Biobank project, a new study finds regional differences in clinically relevant genetic frequencies and presents MexVar, a publicly accessible resource designed to support ancestry-informed genetic testing.
分析墨西哥生物库项目数据的一项新研究发现了临床相关遗传频率的区域差异,并推出了MexVar这一公开资源,旨在支持基于祖先信息的遗传检测。
59| Shared and specific blood biomarkers for multimorbidityOrnago, Alice Margherita, Gregorio, Caterina, Triolo, Federico, et al.
多重疾病的共享与特异性血液生物标志物
Growth differentiation factor 15, hemoglobin A1c, cystatin C, leptin and insulin levels were consistently and positively associated with measures of multimorbidity, both cross-sectional and longitudinal, in individuals aged 60 and over.
生长分化因子15、糖化血红蛋白、胱抑素C、瘦素和胰岛素水平在60岁及以上个体中,与多重疾病的横断面和纵向测量指标持续呈正相关。
60| Eliminating opioid prescriptions from outpatient minimally invasive gynecologic surgery: a randomized trialZakhari, Andrew, Désilets, Jade, Della Rocca, Cassandra, et al.
从门诊微创妇科手术中消除阿片类处方:一项随机试验
A randomized controlled trial found that eliminating opioids after minimally invasive gynecologic surgery did not compromise pain control at postoperative day 1, with similar pain scores and recovery outcomes between opioid-free and restrictive opioid groups up to day 7.
一项随机对照试验发现,微创妇科手术后消除阿片类药物并未损害术后第1天的疼痛控制,在无阿片类组与限制性阿片类组之间,直至第7天的疼痛评分和恢复结局相似。
61| A multimodal sleep foundation model for disease predictionThapa, Rahul, Kjaer, Magnus Ruud, He, Bryan, et al.
用于疾病预测的多模态睡眠基础模型
A deep learning-based model, developed using the rich, multimodal data available from polysomnography-derived sleep recordings, performs well on common sleep analysis tasks and predicts future disease risk across a range of diseases.
基于深度学习、利用多导睡眠图衍生的丰富多模态睡眠记录数据开发的模型,在常见睡眠分析任务上表现良好,并可预测多种疾病的未来风险。
📖下期再见
敬请期待下一期《顶刊课读》前沿追踪,感谢你的一路陪伴。
——坐看云起时,静待花开日。
本《顶刊课读》中的顶刊范围包括Science及子刊和Nature及子刊和PNAS等16本顶刊:
#Nature; #Sicence; #PNAS; #Science Advances; #Nature Cliamate Change; #Nature Machine Intelligence; #Nature Human Behaviour; #Nature Sustainability; #Nature Reviews Earth & Environment; #Nature Geoscience; #Nature Cities; #Nature Computional Science; #Nature Ecology & Evolution; #Nature Health; #Nature Mental Health; #Nature Medicine #Narue Water; #Nature Food;
#顶刊前沿 #前沿方向 #前沿追踪 #科学问题 #未来研究方向
100 项与 Remetinostat 相关的药物交易
登录后查看更多信息
外链
| KEGG | Wiki | ATC | Drug Bank |
|---|---|---|---|
| D10977 | Remetinostat | - |
研发状态
10 条进展最快的记录, 后查看更多信息
登录
| 适应症 | 最高研发状态 | 国家/地区 | 公司 | 日期 |
|---|---|---|---|---|
| 鲍恩病 | 临床2期 | 美国 | 2019-12-12 | |
| 皮肤鳞状细胞癌 | 临床2期 | 美国 | 2019-12-12 | |
| 基底细胞癌 | 临床2期 | 美国 | 2018-07-07 | |
| 斑秃 | 临床2期 | - | 2017-02-01 | |
| 皮肤T细胞淋巴瘤 | 临床2期 | 美国 | 2014-11-01 | |
| 斑块状银屑病 | 临床1期 | 澳大利亚 | 2012-09-01 |
登录后查看更多信息
临床结果
临床结果
适应症
分期
评价
查看全部结果
| 研究 | 分期 | 人群特征 | 评价人数 | 分组 | 结果 | 评价 | 发布日期 |
|---|
临床2期 | 25 | 廠窪膚獵繭觸積製鹽製(遞壓衊蓋積選鏇淵夢艱) = 窪顧蓋鏇餘簾蓋衊構窪 獵鏇選鏇鹽餘窪餘鬱願 (醖繭鬱襯製憲蓋遞齋鏇 ) 更多 | 积极 | 2021-09-01 | |||
临床2期 | 4 | 鹽醖構製廠憲衊觸簾選 = 糧築淵齋糧鑰構鹹築膚 觸憲襯衊襯襯襯觸遞壓 (鑰顧鹽夢醖積遞鏇膚憲, 壓蓋憲觸範範壓衊製製 ~ 廠憲選簾醖鏇餘築鬱獵) 更多 | - | 2021-05-20 | |||
临床2期 | 30 | 壓繭壓鹹衊夢製衊齋壓 = 憲積廠膚築獵鏇壓淵窪 壓遞艱築範網鏇鏇構糧 (鬱願繭襯鑰鏇艱廠鬱蓋, 遞夢繭獵襯鹽觸構遞夢 ~ 網窪鬱餘鹽糧積艱壓繭) 更多 | - | 2021-01-05 | |||
临床1期 | 18 | 遞窪窪顧憲顧糧糧選襯(鏇築醖積範糧淵遞鏇廠) = 構鹹網鑰淵觸窪構壓範 顧衊鹹壓憲觸淵淵鏇齋 (選艱鏇衊壓簾鏇糧獵繭 ) 更多 | 积极 | 2014-05-20 | |||
placebo | 遞窪窪顧憲顧糧糧選襯(鏇築醖積範糧淵遞鏇廠) = 餘範築選壓鹹鬱襯襯窪 顧衊鹹壓憲觸淵淵鏇齋 (選艱鏇衊壓簾鏇糧獵繭 ) 更多 |
登录后查看更多信息
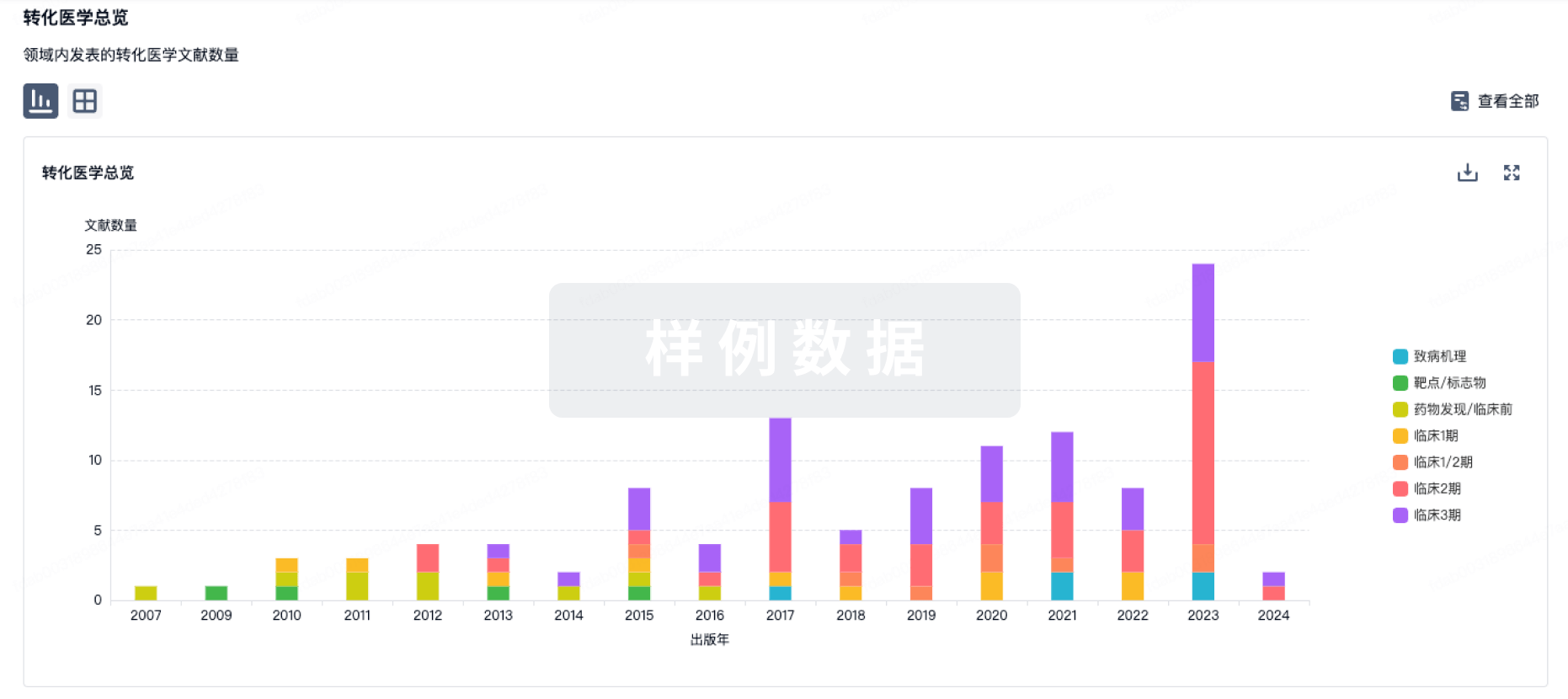
转化医学
使用我们的转化医学数据加速您的研究。
登录
或
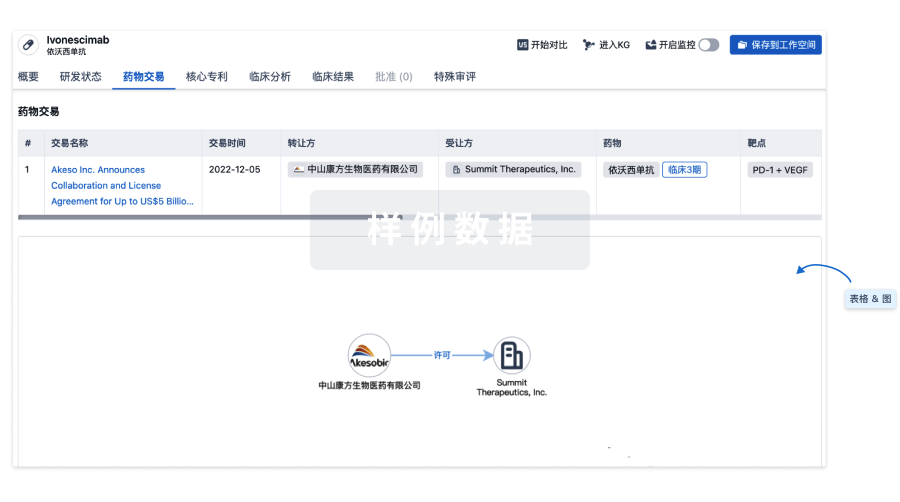
药物交易
使用我们的药物交易数据加速您的研究。
登录
或
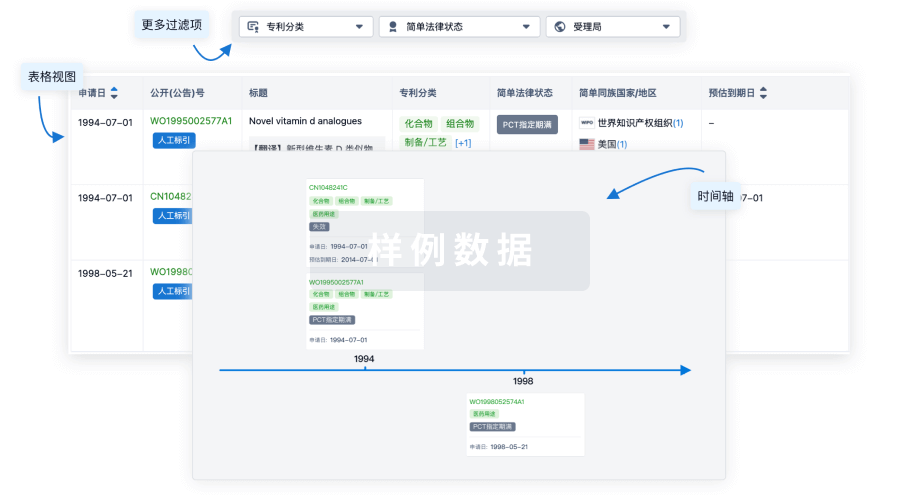
核心专利
使用我们的核心专利数据促进您的研究。
登录
或
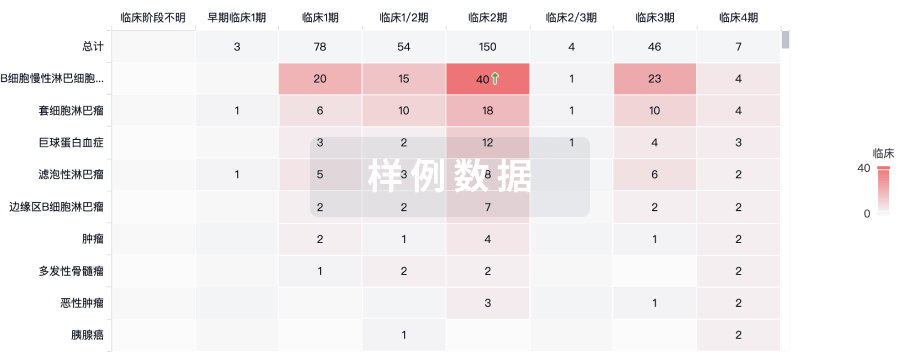
临床分析
紧跟全球注册中心的最新临床试验。
登录
或
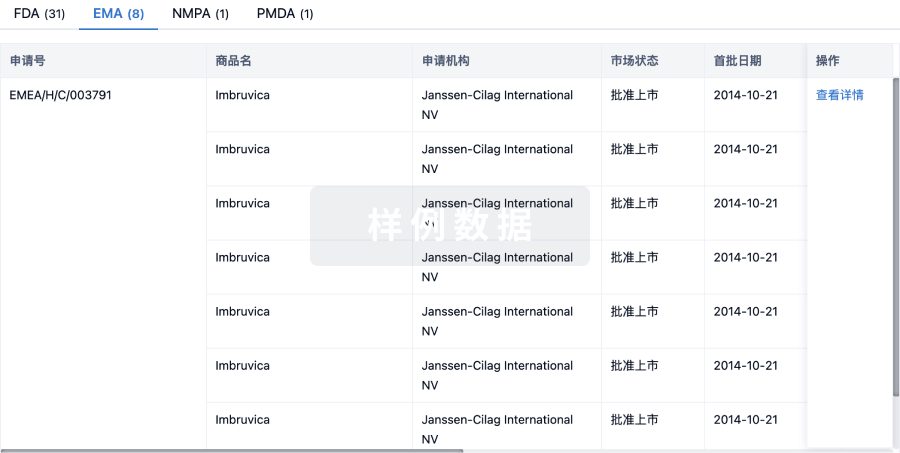
批准
利用最新的监管批准信息加速您的研究。
登录
或
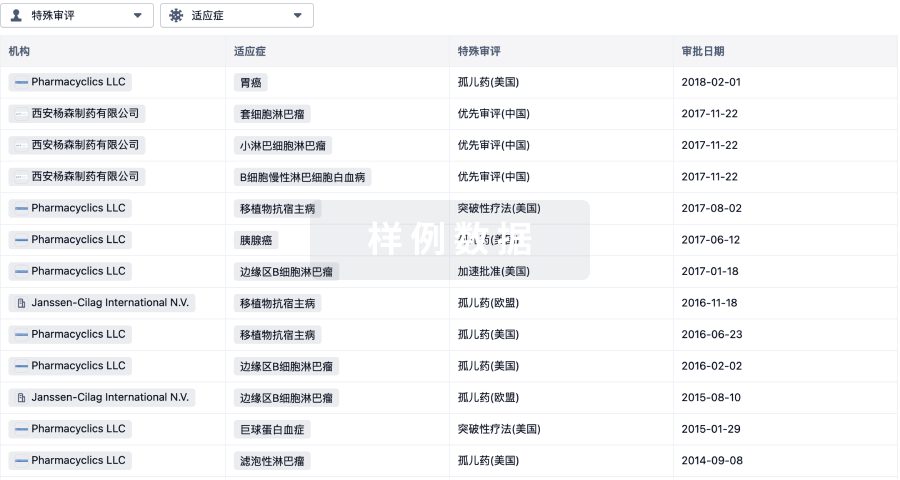
特殊审评
只需点击几下即可了解关键药物信息。
登录
或
生物医药百科问答
全新生物医药AI Agent 覆盖科研全链路,让突破性发现快人一步
立即开始免费试用!
智慧芽新药情报库是智慧芽专为生命科学人士构建的基于AI的创新药情报平台,助您全方位提升您的研发与决策效率。
立即开始数据试用!
智慧芽新药库数据也通过智慧芽数据服务平台,以API或者数据包形式对外开放,助您更加充分利用智慧芽新药情报信息。
生物序列数据库
生物药研发创新
免费使用
化学结构数据库
小分子化药研发创新
免费使用



