预约演示
更新于:2026-02-04

Beijing Institute of Technology
更新于:2026-02-04
概览
标签
其他疾病
肿瘤
神经系统疾病
小分子化药
化学药
重组多肽
疾病领域得分
一眼洞穿机构专注的疾病领域
暂无数据
技术平台
公司药物应用最多的技术
暂无数据
靶点
公司最常开发的靶点
暂无数据
| 排名前五的药物类型 | 数量 |
|---|---|
| 小分子化药 | 13 |
| 化学药 | 2 |
| mRNA | 1 |
| 重组多肽 | 1 |
| 多肽药物 | 1 |
关联
18
项与 北京理工大学 相关的药物靶点 |
作用机制 HER2拮抗剂 |
在研机构 |
原研机构 |
在研适应症 |
非在研适应症- |
最高研发阶段临床前 |
首次获批国家/地区- |
首次获批日期- |
作用机制 AKR1B1抑制剂 [+1] |
在研机构 |
原研机构 |
在研适应症 |
非在研适应症- |
最高研发阶段临床前 |
首次获批国家/地区- |
首次获批日期- |
11
项与 北京理工大学 相关的临床试验NCT07311421
Clinical Study of Non-invasive Blood Glucose Detection Technology Based on Raman Spectroscopy
Diabetes is a chronic metabolic disease that is widely prevalent globally, with its incidence rate continuously increasing, posing significant challenges to patient health and public health systems. In China, the number of diabetes patients ranks first in the world, with an adult prevalence rate as high as 12.8%. The core of diabetes management is blood glucose control. However, traditional finger-prick blood testing methods are inconvenient and have low patient compliance. In recent years, non-invasive blood glucose detection technologies have become a research hotspot. Among them, optical methods, especially spectroscopy techniques, are considered to have the most application potential due to their non-invasive, convenient, and stable characteristics.
Raman spectroscopy, as an important branch of spectroscopy, has advantages such as non-invasiveness and high specificity, and has been successfully applied to blood glucose detection in laboratory settings. However, its clinical application is still in the exploratory stage. Foreign research has validated its feasibility, and domestic research has also made certain progress, but overall, it is still in its infancy. This study aims to compare the consistency and accuracy of Raman spectroscopy non-invasive blood glucose detection with traditional finger-prick blood glucose detection by comparing the blood glucose values measured by the two methods at the same time point. Additionally, the study will assess the participants' satisfaction and acceptance of the two methods through questionnaires. The results of this study will provide a scientific basis for the clinical application of Raman spectroscopy technology and offer references for the promotion of non-invasive blood glucose detection technologies. This will help advance the development of non-invasive blood glucose detection technologies and improve the treatment compliance and quality of life of diabetes patients.
Raman spectroscopy, as an important branch of spectroscopy, has advantages such as non-invasiveness and high specificity, and has been successfully applied to blood glucose detection in laboratory settings. However, its clinical application is still in the exploratory stage. Foreign research has validated its feasibility, and domestic research has also made certain progress, but overall, it is still in its infancy. This study aims to compare the consistency and accuracy of Raman spectroscopy non-invasive blood glucose detection with traditional finger-prick blood glucose detection by comparing the blood glucose values measured by the two methods at the same time point. Additionally, the study will assess the participants' satisfaction and acceptance of the two methods through questionnaires. The results of this study will provide a scientific basis for the clinical application of Raman spectroscopy technology and offer references for the promotion of non-invasive blood glucose detection technologies. This will help advance the development of non-invasive blood glucose detection technologies and improve the treatment compliance and quality of life of diabetes patients.
开始日期2026-01-01 |
申办/合作机构 |
ChiCTR2500106957
Development of lower extremity deep venous valve functional assessment method and the artificial valves based on multi-parameter integration
开始日期2025-07-01 |
申办/合作机构  首都医科大学 首都医科大学 [+2] |
ChiCTR2600116988
Development and Validation of a Multimodal Feature-Based Prediction Model for Post-Dissection Distal Aortic Remodeling Adverse Risk
开始日期2025-01-01 |
申办/合作机构  北京理工大学 北京理工大学 [+1] |
100 项与 北京理工大学 相关的临床结果
登录后查看更多信息
0 项与 北京理工大学 相关的专利(医药)
登录后查看更多信息
22,565
项与 北京理工大学 相关的文献(医药)2026-12-01·Nano-Micro Letters
Multifunctional Three-Dimensional Porous MXene-Based Film with Superior Electromagnetic Wave Absorption and Flexible Electronics Performance
Article
作者: Cao, Maosheng ; Ji, Ying ; Wang, Ziming ; Zhang, Xinci ; Li, Lin ; Zhang, Xitian ; Li, Benyi ; Sun, Gongming ; Liu, Tingting ; Chang, Li
Abstract:
The development of multifunctional electromagnetic wave-absorbing materials is essential for next-generation flexible electronics and intelligent protection systems. Herein, a novel three-dimensional porous MXene-based film integrated with metallic nickel nanoparticles (Ni-PMF) is designed and synthesized with the potential to address the urgent need for multifunctional electromagnetic wave-absorbing materials in next-generation intelligent systems. By using polystyrene spheres as sacrificial templates, a hierarchical porous architecture is constructed to prevent MXene nanosheet restacking, extend electromagnetic wave propagation paths, and optimize impedance matching. Simultaneously, uniformly distributed Ni nanoparticles introduce abundant heterogeneous interfaces, enhancing interfacial polarization and magnetic loss, which significantly improve electromagnetic wave attenuation. The Ni-PMF film achieves a minimum reflection loss of –64.7 dB and a broad effective absorption bandwidth of 7.2 GHz, covering the full Ku-band and outperforming most reported MXene thin film absorbers. In addition to superior electromagnetic wave absorption, the film demonstrates excellent electrothermal conversion and flexible strain-sensing capabilities, enabling integrated protection and real-time sensing functions. This multifunctional material offers promising potential for next-generation smart flexible electronic systems.
2026-12-01·Nano-Micro Letters
Interface Engineering Strategies for Shuttle Mitigation in Alkali Metal–Sulfur Batteries: A Comparative Review from Li–S to Na–S and K–S Systems
Review
作者: Yu, Qiyao ; Chen, Zihan ; Wang, Wei ; Zhang, Jianguo
Abstract:
Rechargeable alkali metal-sulfur (M–S) batteries, including Li/Na/K–S chemistries, have the potential to utilize abundant and low-cost sulfur cathodes yet offer high theoretical energy densities. However, their practical electrochemical performance is fundamentally limited by the polysulfide shuttle effect. This challenge is particularly exacerbated in Na–S and K–S systems owing to larger metal-ion radii, weaker solvation energies, slower redox kinetics, and greater electrolyte–electrode incompatibilities compared to Li–S batteries. This review presents a comparative analysis of interface engineering strategies designed to suppress the shuttle effect across these three systems. Following a summary of sulfur cathode properties and reaction mechanisms, we systematically examine the origins of polysulfide shuttling. Our analysis progresses from functional separator design and interlayer enhancements to the implementation of solid‑state electrolytes for root-cause inhibition. By evaluating interface engineering research specific to Na–S and K–S batteries, we elucidate both shared principles and unique challenges inherent to alkali M-S systems. Finally, we propose multifaceted solutions to achieve shuttle-free operation and enhance overall battery performance, thereby establishing a foundation for future advancements.
2026-06-01·NEURAL NETWORKS
Rotation equivariant quantum graph neural networks with trainable compression encoder and entanglement-enhanced aggregation
Article
作者: Liu, Wenjie ; Zhu, Yifan ; Liu, Weiwei ; Du, Bohan
The integration of symmetry, such as permutation equivariance, into Quantum Graph Neural Networks (QGNNs), referred to as Equivariant Quantum Graph Neural Networks (EQGNNs), markedly improves the model's generalization performance on graph-structured data. Despite this advancement, current research has not yet extended rotational equivariance to QGNN frameworks. Furthermore, processing large-scale graph data increases computational complexity due to numerous inter-node connections, significantly raising the required number of qubits. To address these challenges, a novel Rotationally Equivariant Quantum Graph Neural Network (REQGNN) with trainable compression encoder and entanglement-enhanced aggregation mechanism is proposed. By adopting quantum fidelity as the evaluation metric, we design a quantum autoencoder to effectively compress feature dimensionality, substantially lowering the qubit requirements of the model while preserving essential global structural details. To achieve rotational equivariance in the model, we propose an entanglement-enhanced layer that incorporates distance and angle information between nodes. This layer performs entanglement by extracting diverse edge information, thereby further refining edge feature extraction. Additionally, an auxiliary entanglement layer is introduced to mitigate the over-smoothing issue. Experimental results demonstrate REQGNN is significantly better for graph classification tasks than GIN, Gra+QSVM, and Gra+QCNN on four datasets in all metrics and achieves better results than egoGQNN in accuracy on PTC dataset, and it also has advantage for graph regression tasks over the classical models, including EGNN and EquiformerV2, and reduces the MAE of Cv task unit by 20% on average compared with a previous quantum model QGCNN. Our approach offers an effective solution for achieving rotational equivariance while providing a novel perspective for exploring symmetry in graph neural networks (GNNs).
161
项与 北京理工大学 相关的新闻(医药)2026-02-01
点击卡片 关注我们
Interdisciplinary MEDICINE(IMed)交叉医学期刊第四卷第一期于2026年1月30日正式上线!本期共收录14篇文章,包含7篇论著、7综述(Review)。全部论文均为开放获取,供广大读者免费阅读!
Interdisciplinary Medicine (IMed) Volume 4, Issue 1 was officially launched on January 30, 2026! This issue features 14 articles, including 7 research articles and 7 reviews. All papers are open access and freely available to all readers.
欢迎登录IMed期刊主页,或点击底部阅读原文浏览第四卷第一期全文:
https://onlinelibrary.wiley.com/toc/28326245/2026/4/1
Welcome to visit the IMed journal homepage or click on the "Read More" link at the bottom to browse the full text of Volume 4, Issue 1: https://onlinelibrary.wiley.com/toc/28326245/2026/4/1
Front Cover
Back Cover
Frontispiece
滑动查看本期封面图片
IMed Volume 4 Issue 1
IMed 内容概览
IMed第四卷第一期共发表文章14篇,包含7篇Research Article以及7篇Review。由来自于中国、澳大利亚、新加坡、沙特阿拉伯 等 科学家们针对不同学科的前沿问题发表了最新的研究成果。
01 封面论文
重庆医科大学附属第一医院 Lai Xiaofei(赖晓霏) 教授团队发表综述文章, 标题是:基于微流控技术的肠道菌群检测研究进展(Progress in the detection of gut microbiota based onmicrofluidic technology)。DOI: 10.1002/inmd.70069。肠道菌群作为人体肠道内的复杂微生物群落,对消化、营养吸收及免疫调节至关重要,其组成、结构与功能的精准检测是解析健康 - 疾病关联、实现疾病早诊与个性化治疗的关键。传统检测方法存在显著局限 —— 培养法依赖特定培养基,难以分离厌氧和苛养微生物且检测周期长,常规聚合酶链式反应(PCR)操作复杂、通量低且易污染,无法满足高效、精准、高通量的分析需求。微流控技术通过微尺度通道操控微量流体,具备操作简便、试剂消耗少、分析快速等优势,为肠道菌群检测提供了全新技术路径。本文系统综述了近年来基于微流控技术的肠道菌群检测方法,涵盖分离类、核酸分析类、免疫分析类、成像类及微环境模拟类五大技术类型,详细阐述了各类技术的核心原理,分析了其在实际应用中的成果、优势与局限性。
文章链接二维码(QR code for article link)
02 第二篇文章
新加坡南洋理工大学 Paulo Bartolo 教授 团队发表综述文章, 标题是:基于光固化立体成型(VP)的生物 3D 打印:用光塑造下一代组织(Vat photopolymerization-based bioprinting: Shaping next-generation tissues with light)。DOI: 10.1002/inmd.70078 在组织工程与再生医学领域,功能组织的制造是核心挑战,天然组织具备复杂的微结构、细胞异质性和精准空间组织,这对复刻其生理功能至关重要。传统组织构建方法存在显著局限 —— 支架细胞接种法难以还原天然组织的精细微环境,挤出式生物打印分辨率有限,喷射式打印虽通量较高但构建体机械强度不足,均无法满足高性能组织工程的需求。光固化立体成型(VP)生物 3D 打印作为变革性技术,通过光介导交联实现微米级精度控制,具备几何保真度高、结构复杂度高、制造速度快等独特优势,为精准制造载细胞组织构建体提供了全新路径。本文系统综述了 VP 生物 3D 打印的最新进展,围绕光聚合化学、打印模式、生物墨水设计和生物医学应用四大核心主题,详细阐述了链增长、逐步增长、光介导氧化还原等光聚合机制,立体光刻(SLA)、数字光处理(DLP)、双光子聚合(TPP)、体积增材制造(VAM)等关键打印技术的原理与适用性,分析了生物墨水(功能单体、光引发剂、光吸收剂)的设计标准(细胞相容性、流变学 / 光学特性、机械性能等),并探讨了该技术在骨、心脏、软骨、角膜、肝脏等组织工程中的应用,同时展望了多材料 / 多模式打印、机器学习优化、临床转化监管等前沿趋势,为 VP 技术向临床可行、高通量组织工程技术发展提供了路线图。
文章链接二维码(QR code for article link)
03 第三篇文章
澳大利亚 格里菲斯大学 Peyman Halvaeikhanekahdani 教授团队发表综述文章, 标题是:纳米颗粒整合型电刺激响应生物材料:临床再生医学中药物递送与组织修复的创新(Nanoparticle‐integrated electrostimulation‐responsive biomaterials: Innovations in drug delivery and tissue repair in clinical regenerative medicine)。DOI: 10.1002/inmd.70077 组织工程在修复受损组织和器官方面具有巨大潜力,但现有方法常因宿主整合性差、药物递送精度有限、可扩展性不足等问题难以满足临床需求。传统治疗策略如手术干预、组织移植和药物治疗,虽能缓解部分症状,却存在供体短缺、免疫排斥、恢复周期长等显著局限,无法实现组织功能的完全修复。电刺激响应生物材料与纳米颗粒的结合为解决这些难题提供了全新路径 —— 电刺激可调控细胞代谢、增殖、分化等关键过程,纳米颗粒则能增强局部治疗递送效率,二者协同作用可显著提升再生效果。
文章链接二维码(QR code for article link)
04 第四篇文章
陆军军医大学西南医院包静 教授 团队发表综述文章, 标题是:战场创伤病原细菌即时检测(POCT)的进展与挑战(Advances and challenges in point‐of‐care testing for pathogenic bacteria in battlefield injuries)。DOI: 10.1002/inmd.70071 感染是战场创伤患者延迟死亡的主要原因,实时、准确、快速检测侵入性病原菌对优化伤口管理、加速康复至关重要。传统诊断方法存在显著局限 —— 细菌分离培养、核酸扩增等技术需精密设备和专业人员操作,检测周期长,无法在资源有限、高应激的战场环境中实现快速多重病原菌检测,难以满足战地救治的即时诊断需求。床旁检测(POCT)生物传感器具有便携性强、功能多样的特点,无需依赖中心化实验室即可实现现场诊断,为战地病原菌检测提供了全新技术路径。
文章链接二维码(QR code for article link)
05 第五篇文章
北京理工大学 陆梅 教授 团队发表综述文章, 标题是:基于细胞外囊泡(EVs)的癌症疫苗与免疫治疗剂(Extracellular vesicle‐based vaccines and immunotherapeutics for treatment of cancer)。DOI: 10.1002/inmd.70084 癌症免疫治疗因疗效持久、副作用小且能靶向肿瘤异质性,已成为癌症治疗的重要方向,而疫苗与免疫治疗剂是其核心模态。传统治疗及免疫疗法存在显著局限 —— 手术、放化疗副作用强,肽疫苗易发生抗原缺失突变,单克隆抗体易引发耐药性,免疫检查点抑制剂效果有限且缺乏精准递送系统,难以高效激活抗肿瘤免疫。细胞外囊泡(EVs)作为天然纳米级囊泡,具有独特优势:可展示多种抗原和免疫刺激分子,生物相容性佳、能穿透生物屏障,还可递送 RNA、蛋白质、化疗药物等多种治疗剂,为癌症免疫治疗提供了全新的无细胞平台。
文章链接二维码(QR code for article link)
06 第六篇文章
广州医科大学李莹教授,标题是:聚集诱导发光分子(AIEgens)在体外诊断中的应用:推进体液中生物标志物检测(Aggregation‐induced emission luminogens in in vitro diagnostics: Advancing biomarker detection in body fluids)。DOI: 10.1002/inmd.70066体液中生物标志物的快速、灵敏、准确检测是健康监测与疾病早诊、疗效评估的关键。传统荧光检测技术存在显著局限 —— 常规荧光探针在聚集状态下易发生荧光猝灭,光稳定性差,且受生物样本自身 autofluorescence 干扰大,操作复杂且依赖大型仪器,难以满足微量生物标志物的精准检测及即时诊断需求。聚集诱导发光分子(AIEgens)作为新型荧光材料,具有独特优势:在聚集或固态下发光增强,光稳定性高、结构可修饰性强,可通过特异性相互作用识别目标标志物,为体液检测提供了全新技术路径。
文章链接二维码(QR code for article link)
07 第七篇文章
陆军军医大学第二附属医院邱远 教授 团队联合中南大学发表综述文章, 标题是:炎症性肠病(IBD)的代谢重编程-从病理机制到靶向干预(Inflammatory bowel disease and metabolic reprogramming: From pathological mechanisms to targeted interventions)。DOI: 10.1002/inmd.70083 炎症性肠病(IBD)包括克罗恩病和溃疡性结肠炎,是遗传易感性、环境暴露、免疫失调与肠道菌群紊乱共同作用的结果,其慢性复发特征严重影响患者生活质量,解析发病机制并开发精准干预策略至关重要。传统治疗存在显著局限 —— 糖皮质激素、免疫调节剂及生物制剂等虽能缓解症状,但易引发耐药性、感染风险等副作用,且未能针对 IBD 核心的代谢紊乱问题,难以实现长期缓解。代谢重编程作为 IBD 发病的核心特征,为疾病干预提供了全新技术路径 —— 免疫细胞与肠道上皮细胞的糖酵解、脂肪酸代谢及氧化磷酸化紊乱,会影响免疫细胞极化与肠屏障完整性,而肠道菌群衍生的短链脂肪酸、胆汁酸等代谢物可通过调控相关受体与信号通路调节炎症反应。本文系统综述了 IBD 免疫代谢领域的最新进展,详细阐述了免疫细胞、肠道上皮细胞的代谢重编程机制,分析了肠道菌群衍生代谢物的调控作用,探讨了微生物调节、代谢物补充、AMPK/mTOR 等代谢通路靶向等干预策略,总结了疾病异质性、靶向递送不足等当前挑战,为 IBD 的精准治疗提供了全面参考。
文章链接二维码(QR code for article link)
08 第八篇-论著文章
南方医科大学公共卫生学院周晓红教授 团队联合广州市疾病预防控制中心发表Research Article, 标题是:基于 CRISPR/Cas12a 的重组酶辅助扩增(RAA)检测方法-用于蚊子和临床样本中登革热病毒的快速监测,助力全球协同监测与风险评估以阻断登革热传播(A clustered regularly interspaced palindromic repeat‐Cas12a‐based assay for rapid dengue virus monitoring in mosquito and clinical samples facilitating global collaborative surveillance and risk assessment to block dengue spreading)。DOI: 10.1002/inmd.70074 登革热是由登革热病毒(DENV)引起的伊蚊传播急性传染病,全球流行态势严峻,快速精准的监测对疫情防控至关重要。传统检测方法存在显著局限 ——RT-PCR 技术耗资源、耗时,依赖专业设备,难以在基层医疗机构推广;血清学方法灵敏度和特异性较低,且无法满足跨区域、多样本的高效监测需求,制约了登革热的早期预警与疫情阻断。基于 CRISPR/Cas12a 的重组酶辅助扩增(RAA-Cas12a)技术为解决这些难题提供了全新路径,该技术兼具高灵敏度与特异性,通过 37℃温和扩增无需复杂仪器,检测快速且操作简便。。
文章链接二维码(QR code for article link)
09 第九篇-论著文章
暨南大学医学院生理学系 代小勇教授 团队发表Research Article, 标题是:抗 CD47 抗体修饰的载顺铂介孔二氧化硅纳米颗粒用于结直肠癌患者来源类器官异种移植模型的靶向化学免疫治疗(Anti‐CD47 antibody‐decorated and cisplatin‐containing mesoporous silica nanoparticles for targeted chemoimmunotherapy of colorectal cancer in a patient‐derived organoids xenograft model)。DOI: 10.1002/inmd.70075 结直肠癌(CRC)是全球高发恶性肿瘤,一线放化疗与免疫治疗存在明显局限 —— 化疗药物(如顺铂)缺乏肿瘤特异性,脱靶毒性强(易损伤肝肾、骨髓等)且易引发耐药性;免疫治疗则受限于 “冷肿瘤” 微环境,肿瘤细胞过表达 CD47 分子可通过结合巨噬细胞表面 SIRPα 蛋白逃避免疫监视,导致治疗效果不佳。基于介孔二氧化硅纳米颗粒(MSN)的靶向纳米递送系统为解决上述难题提供了全新路径,该载体兼具高载药能力与可控缓释特性,结合抗体靶向修饰可实现精准递药与免疫调节协同作用。本文构建了载顺铂(CDDP)并修饰抗 CD47 抗体的纳米复合物(CDDP@MSN‐Anti),系统验证其治疗效果:通过抗 CD47 抗体精准靶向 CRC 细胞,MSN 实现顺铂缓释,诱导活性氧过量产生并激活 caspase‐3 相关凋亡通路,同时释放损伤相关分子模式(DAMPs)促进肿瘤相关巨噬细胞(TAMs)从 M2 型向抗炎杀瘤的 M1 型极化,恢复巨噬细胞吞噬活性;在 CRC 细胞系、患者来源类器官及异种移植模型中,该复合物均展现出强效抑瘤效果,显著降低系统毒性,延长荷瘤小鼠生存期,为 CRC 精准化学免疫治疗提供了新型策略与实验依据。
文章链接二维码(QR code for article link)
10 第十篇-论著文章
同济大学医学院附属东方医院 陈波 教授 团队发表Research Article,标题是:整合磁性纳米颗粒的纳米工程化中性粒细胞用于 T₂加权磁共振成像引导的胰腺癌增强磁热治疗(Nanoengineered neutrophils integrated with magnetic nanoparticles for T₂‐weighted magnetic resonance imaging‐guided enhanced magnetic hyperthermia therapy of pancreatic tumor)。DOI: 10.1002/inmd.70061 胰腺癌是致死率极高的恶性肿瘤,5 年生存率不足 10%,传统治疗面临诸多局限 —— 手术切除难度大、放化疗易产生耐药性,且胰腺癌所处的深部位置与 immunosuppressive 肿瘤微环境,导致常规磁热治疗(MHT)靶向性差、温度控制难,易造成脱靶损伤。纳米工程化中性粒细胞(NE)与磁性纳米颗粒结合的协同治疗策略为解决上述难题提供了全新路径,中性粒细胞具备天然肿瘤归巢能力,可穿透致密肿瘤基质,磁性纳米颗粒则能实现磁热消融与影像引导双重功能。本文构建了负载 Fe₃O₄@PEI@PDA(FPP)磁性纳米颗粒的纳米工程化中性粒细胞(FPPN),系统验证其治疗效果:FPPN 借助中性粒细胞的肿瘤靶向性,显著提升肿瘤部位纳米颗粒富集度;在 T₂加权磁共振成像(MRI)引导下,可精准定位肿瘤并监控治疗过程;交替磁场作用下,FPP 产生 42-45℃治疗温度直接消融肿瘤细胞,同时磁热激活中性粒细胞线粒体产生大量活性氧(ROS),通过 “磁热消融 + ROS 杀伤” 协同增强抗肿瘤效果;在胰腺癌动物模型中,FPPN 治疗组肿瘤消融效果显著,且无明显肝肾毒性,为深部肿瘤的精准靶向治疗提供了新型技术平台。
文章链接二维码(QR code for article link)
11 第十一篇-论著文章
吉林大学免疫学院 闫东梅 教授团队发表Research Article,标题是:靶向肿瘤相关巨噬细胞中的缺氧诱导因子 - 1α- 外泌体血管内皮生长因子轴克服卡介苗免疫治疗耐药性(Targeting the hypoxia‐inducible factor‐1 alpha‐exoVEGF axis in tumor‐associated macrophages overcomes Bacillus Calmette‐Guérin immunotherapy resistance)。DOI: 10.1002/inmd.70063卡介苗(BCG)免疫治疗是膀胱癌等肿瘤的重要临床方案,但约 50% 患者会出现耐药,其核心瓶颈在于肿瘤微环境(TME)异常血管生成削弱免疫疗效。传统治疗缺乏针对耐药机制的精准干预策略 ——BCG 激活的肿瘤相关巨噬细胞(TAMs)会通过未知通路促进血管生成,导致肿瘤逃逸,现有方案无法靶向该关键环节。靶向 HIF-1α-exoVEGF 轴的干预策略为突破耐药提供了全新技术路径,缺氧诱导因子 - 1α(HIF-1α)可调控巨噬细胞分泌血管内皮生长因子(VEGF)并封装进外泌体(exoVEGF),进而驱动血管生成,这一轴通路是 BCG 耐药的核心机制。本文系统验证了该机制及干预效果:BCG 通过激活 NF-κB、PI3K/AKT 等通路上调巨噬细胞 HIF-1α 表达,促进 VEGF 分泌及外泌体封装,外泌体介导 VEGF 递送并激活内皮细胞血管生成;巨噬细胞特异性敲除 HIF-1α 可显著抑制 BCG 诱导的血管生成,不影响 CD8+T 细胞、B 细胞浸润,同时增强 BCG 的抗肿瘤效果;沉默外泌体中的 VEGF 可削弱其促血管生成活性。该研究揭示了 BCG 免疫治疗耐药的关键机制,为靶向 HIF-1α-exoVEGF 轴的联合治疗策略提供了实验依据。
文章链接二维码(QR code for article link)
12 第十二篇-论著文章
香港理工大学应用生物与化学科技学系 Shakeel Ahmad Khan 教授 团队联合沙特国王科技大学控制与仪器工程系 Adnan Shakoor 博士 团队发表Research Article,标题是:TargetGen‐RNN 模型发现靶向耐药金黄色葡萄球菌的新型抗生素化合物(TargetGen‐RNN model discovers novel antibiotic compound targeting drug‐resistant Staphylococcus aureus)。DOI: 10.1002/inmd.70064 耐甲氧西林金黄色葡萄球菌(MRSA)等耐药菌感染已成为全球健康危机,现有抗生素因耐药性疗效锐减,而传统抗生素发现方法存在显著局限 —— 高通量筛选命中率低、耗时耗力,基于结构的药物设计易受蛋白‐配体相互作用建模复杂性限制,天然产物筛选常重复发现已知化合物,难以获得具有新型骨架的靶向化合物。深度学习驱动的生成模型为突破这一瓶颈提供了全新技术路径,可通过数据驱动方式探索化学空间,高效生成结构新颖且具有生物活性的化合物。本文开发了 TargetGen‐RNN 深度生成学习模型,通过迁移学习、温度调制采样及严格化学验证,基于 570 万种药物样化合物预训练,结合 82 种已知金黄色葡萄球菌二氢叶酸还原酶(DHFR)抑制剂微调,生成 28708 种结构多样的新型化合物;经 QSAR 分析、药效团映射、分子对接、分子动力学模拟等虚拟筛选,发现新型骨架抗生素 SAK‐2970。该化合物具有良好的药代动力学特性,体外对金黄色葡萄球菌表现出强效杀菌活性,能有效抑制并清除生物膜,对环丙沙星耐药菌株同样高效;在耐药菌败血症小鼠模型中,可显著降低体内菌载量、提高存活率,且系统毒性极低。该研究验证了 SAK‐2970 作为耐药菌感染治疗候选药物的潜力,同时证明 TargetGen‐RNN 模型在新型抗生素发现中的高效性,为对抗抗菌药物耐药性提供了新策略。
文章链接二维码(QR code for article link)
13 第十三篇-论著文章
南方医科大学基础医学院生物信息学系余光创教授发表Research Article,标题是:Illumina NovaSeq 6000 与 GeneMind SURFSeq 5000 平台在小鼠脑和肺单细胞空间转录组学中的比较(Comparison of Illumina NovaSeq 6000 and GeneMind SURFSeq 5000 platforms for single‐cell spatial transcriptomics of mouse brain and lung)。DOI: 10.1002/inmd.70067 单细胞空间转录组学可在保留组织空间结构的前提下实现基因表达全景分析,是解析复杂组织细胞异质性与空间组织规律的关键技术,其数据质量高度依赖测序平台性能。传统测序平台存在显著局限 ——Illumina NovaSeq 6000 作为行业标准,虽性能稳定但购置与运行成本高昂,限制了该技术的广泛普及,而新型替代平台的适用性与可靠性缺乏系统验证。直接对比评估不同测序平台的兼容性与性能,为空间转录组学研究提供低成本、高质量的技术选择,成为当前研究的重要需求。本文通过 SeekSpace 单细胞空间转录组学技术,对小鼠脑和肺组织的相同 cDNA 文库,分别在 Illumina NovaSeq 6000 与 GeneMind SURFSeq 5000 平台进行测序,采用统一生物信息学流程分析。结果显示,SURFSeq 5000 在独特分子标识符(UMI)捕获、空间条形码检测、基因识别及映射率等核心指标上,与 NovaSeq 6000 表现高度一致;下游的降维聚类、细胞类型注释、空间映射、差异基因表达、细胞间相互作用及空间热点模块检测等分析中,两种平台的结果高度吻合,差异基因重叠率约 65%,细胞类型分配重现性优异(受试者工作特征曲线下面积 > 0.92),且无明显批次效应。该研究证实 GeneMind SURFSeq 5000 是 Illumina NovaSeq 6000 可靠且经济的替代方案,为空间组学研究提供了更具可及性的技术选择,助力该领域的广泛发展。
文章链接二维码(QR code for article link)
14 第十四篇-论著文章
广州中医药大学第三附属医院骨科何伟教授 团队发表Research Article,标题是:模仿斗拱结构的 3D 打印支架通过调控炎症与力学刺激促进骨软骨再生(Mimicking DOUGONG brackets orchestrate regulating inflammation and mechanical stimuli for osteochondral regeneration using 3D printing)。DOI: 10.1002/inmd.70068骨软骨缺损是骨科常见难治疾病,软骨因缺乏血管、神经分布导致自我修复能力极差,且常伴随软骨与软骨下骨同时损伤,严重影响关节功能。传统治疗方法存在显著局限 —— 微骨折术修复组织不稳定,软骨移植易引发免疫排斥,人工关节置换术后并发症多,单一生物材料支架则难以兼顾力学支撑、成骨成软骨活性及炎症调控需求。模仿传统建筑 “斗拱” 结构的 3D 打印复合支架,为骨软骨再生提供了全新技术路径 —— 斗拱的多层嵌套与榫卯结构可模拟骨软骨组织的力学传递特性,结合功能生物材料的协同作用,实现力学支撑与生物活性的双重优化。本文通过 3D 打印技术制备 β- 磷酸三钙、镁黄长石(AKer)与不同浓度硅酸锶(SrSiO₃)的复合支架,系统验证其修复效果:AKer/Sr5% 支架孔隙均匀、孔隙率高,力学性能优异且能持续释放锶离子;体外实验中,该支架显著提升骨髓间充质干细胞活力与增殖能力,抑制凋亡,上调成骨标志物(RUNX2、COL1A1、OCN、OPN),下调炎症因子(IL-6、TNF-α),同时促进软骨细胞表型维持(上调 COL2A1、SOX9);在 SD 大鼠膝骨关节骨软骨缺损模型中,该支架在骨体积、骨密度及组织修复评分上表现最优,通过 PI3K/Akt 信号通路促进成骨,借助细胞因子 - 细胞因子受体相互作用调控炎症,实现骨软骨协同再生。该研究为骨软骨修复的临床转化提供了理论基础与创新策略。
文章链接二维码(QR code for article link)
欢迎关注Imed期刊
期刊简介
IMed
扫二维码
关注期刊官微
Interdisciplinry MEDICINE (IMed)是由南方医科大学南方医院与WILEY出版集团联合创办的一本开放获取学术期刊。IMed致力于报道以多学科交叉为研究手段的医学创新科研成果。IMed期刊已被DOAJ、CAS、Scopus、ESCI数据库收录,2025年6月获得第一个影响因子13.6,在Medicine,Research&Experimental(医学,研究&实验)学科领域内位于Q1区(排名5/195)。期刊秉承标准Peer-Review流程,稿件处理及时,并为优秀文章提供免费文章摘要制作和宣传推广。
2025年Imed期刊文章目录回顾
IMed第三卷第六期正式上线!IMed Volume 3, Issue 6 is now officially live!
IMed编辑部,公众号:Interdisciplinary MEDICINEIMed第三卷第六期正式上线!IMed Volume 3, Issue 6 is now officially live!
IMed第三卷第五期正式上线!IMed Volume 3, Issue 5 is now officially live!
IMed编辑部,公众号:Interdisciplinary MEDICINEIMed第三卷第五期正式上线!IMed Volume 3, Issue 5 is now officially live!
IMed第三卷第四期正式上线!IMed Volume 3, Issue 4 is officially live!
IMed编辑部,公众号:Interdisciplinary MEDICINEIMed第三卷第四期正式上线!IMed Volume 3, Issue 4 is officially live!
IMed第三卷第三期正式上线!IMed Volume 3, Issue 3 is officially live!
IMed编辑部,公众号:Interdisciplinary MEDICINEIMed第三卷第三期正式上线!IMed Volume 3, Issue 3 is officially live!
IMed第三卷第二期正式上线!IMed Volume 3, Issue 2 is officially live!
IMed编辑部,公众号:Interdisciplinary MEDICINEIMed第三卷第二期正式上线!IMed Volume 3, Issue 2 is officially live!
IMed第三卷第一期正式上线!
IMed编辑部,公众号:Interdisciplinary MEDICINEIMed第三卷第一期正式上线!
IMED每期论文合集
关于投稿
SUBMISSION
非常高兴地邀请交叉医学领域专家学者向IMed投稿。我们相信您的支持将与本刊共同推动交叉医学领域的融合创新发展。
发表文章类型:Research Article、Review、Perspective、Short Communication、Letter to the Editor、Standard、Position Paper、Editorial
IMed主页:
https://onlinelibrary.wiley.com/journal/28326245
投稿网站:
https://onlinelibrary.wiley.com/page/journal/28326245/homepage/author-guidelines
邮箱:intmed@smu.edu.cn
X (previousTwitter):@Medicineln17771
编辑丨龚英
初审丨司徒博
审定丨郑磊
临床1期微生物疗法
2026-01-26
·今日头条
> 2026年北京两会期间,作为全国首个医药健康产业规模破万亿的城市,北京如何破解创新药从实验室到临床的转化难题,成为政协委员们热议的焦点。多位委员从数据整合、支付协同、机制革新等多维度,探讨了一套旨在提升研发效率与可及性的“北京方案”。

1. 中医创新:跨院数据整合与AI赋能
北京市政协委员、北京中医药大学“大学未来学习中心”副主任闫永红指出,北京拥有中国中医科学院、北京中医药大学、同仁堂等顶尖机构和品牌,具备显著的人才优势,但关键在于将优势转化为落地成果。
她建议,针对某一类疾病,组建跨医院的研发团队,整合多家医院现有数据,并统一未来数据收集的标准,以构建高质量、规范化的临床数据库。
在中药创新药研发上,AI有望成为不可或缺的工具。闫永红以研究天然牛黄的质量评价为例,表示正在利用数据建模和算法进行分析,人工智能能够科学、高效地处理海量临床数据,并通过建模加速研发过程。她相信,通过真实世界数据与人工智能的结合,**有望将新药研发周期缩短至少三年**。
> “目前国内中药创新研发领先的企业,如康缘、以岭等,其成功模式正是做到了与高校、科研机构的深度融合发展。因此,北京应当进一步推动‘产学研用’深度融合,在政策、研发技术、合作模式上协同创新,才能真正将潜力转化为实力。”
2. 支付保障:多层次医保协同破解“用不起”
创新药研发成功后,支付问题成为落地“最后一公里”的关键。北京市政协委员、赛诺菲大中华区副总裁朱海鸾提交提案,建议完善多层次医疗保障协同机制,推动创新药更好落地。

她指出,当前基本医疗保险、商业健康保险等多种保障方式在功能定位、支付规则等方面存在衔接不足,影响了创新药规范落地和可及性提升。
2026年,北京已在行动。**“北京普惠健康保”特药清单增加到159种**,涵盖国内上市特药57种、海外上市国内暂未上市特药65种,还新增37种创新药品及创新疗法、高值慢病用药,首次将CAR-T疗法等纳入保障范围。该产品提供累计保额350万元,特药责任0免赔,健康人群报销比例提高至65%。
首版《商业健康保险创新药品目录》纳入19种药品,包括CAR-T等肿瘤治疗药品和罕见病治疗药物,与基本医保形成互补。例如,神经母细胞瘤药物那西妥单抗注射液,通过北京惠民保可报销35%的药费,减轻患者负担。
国家医保局正探索商保与基本医保错位发展,给予“三除外”支持政策,如不纳入基本医保自费率指标等。
3. 机制革新:创新联合体激活全链条
为打通“基础研究-技术攻关-产业应用-人才培养”全链条,北京市政协委员、中国工程院院士、北京工业大学校长聂祚仁建议,由市级层面统筹,实体化组建一批“高校-科研机构-领军企业”创新联合体。核心是推动机制革新:
- 建立创新要素共享平台,推动重大科研设施、科学数据与仪器设备开放共享。
- 深化人才评价与流动改革,试点科研人员“旋转门”制度。
- 创新项目形成机制,试点推行“企业出题、联合答题、市场验题”模式。
北京已成功支持组建了**27个覆盖人工智能、量子信息等领域的创新联合体**。例如,盟固利新材料牵头组建先进动力电池创新联合体,包括北京理工大学及产业链企业。房山区良乡大学城推动25项科技成果就地转化,并搭建科创公共服务平台。
4. 审评提速:政策优化加速上市
在审评审批环节,国家药监局进一步优化临床急需境外已上市药品审评审批机制,鼓励全球同步研发、同步申报上市,对于符合要求的可纳入优先审评审批范围。药审中心对纳入优先审评审批范围的注册申请予以单独管理,加强沟通指导。
北京市政协委员杨伟宪建议,优化集采与目录动态调整机制,建立基于临床价值的科学透明评审谈判机制,实现“优质优价”动态管理,以平衡可及性与创新性。
5. 协同破局:从“散珠”到“项链”
“北京方案”的核心在于协同破局,将政企学研的优势拧成合力。从数据整合到支付协同,从创新联合体到政策优化,每一个环节的优化都在为创新药研发注入新动能。随着这些措施的落地,北京不仅有望在国内发挥引领作用,更将在全球医药创新版图中占据重要位置。
对于患者而言,未来可能是更多创新药可及、可负担的现实。这不仅是“接地气”的解决办法,更是北京利用其独特资源,推动医药健康产业高质量发展的智慧体现。
细胞疗法免疫疗法
2026-01-26
·今日头条
> 北京成为全国首个医药健康产业规模突破1万亿元的城市,标志着其在生物医药领域取得了规模上的领先地位。
然而,在这张亮眼的成绩单背后,新药研发著名的 “双十定律”——即平均需要十年以上时间和十亿美元以上资金,且失败率超过90%——所伴随的漫长周期与高昂成本风险,以及科技成果从实验室到病床的转化难题,仍是产业升级面临的主要瓶颈。
1. 政策与成本优势构筑产业基石
北京医药健康产业的万亿突破并非偶然。政策端,北京已**接续实施三轮加快医药健康协同创新行动计划**,并在2024-2025年连续出台《北京市支持创新医药高质量发展若干措施》,为创新药发展注入持续动能。
在创新赛道上,北京正纵深布局**人工智能+医药健康、细胞基因治疗、脑机接口**等前沿领域。
更为突出的优势体现在研发效率与成本上。中国已成为全球药企眼中 **“性价比极高的合作对象”**。具体数据显示:
- 在**I期临床阶段**,美国的平均患者入组时间超过18个月,而中国仅需8个月。
- 在**III期临床阶段**,美国招募单例受试者的平均成本为7万美元,而在中国,这一数字仅为**2.5万美元**。
- 整体上,中国单例患者的临床试验成本为4-7万美元,而全球多中心临床实验的平均成本高达12-18万美元,相差三倍以上。
这种优势源于中国庞大的患者基数、覆盖广泛的医院网络以及丰富的临床资源,而非简单的劳动力成本差异。
2. 光环下的挑战:转化、竞争与支付之困
尽管产业规模与成本优势显著,但北京的创新药研发仍面临多重深层挑战。
**首先是科技成果转化的“最后一公里”梗阻。** 高校普遍存在 **“不能转、不敢转、不会转”** 的难题。北京理工大学技术转移中心副主任陈柏强指出,大多数高校的成果转化流程可能要耗时半年甚至一年,“企业哪经得起等待”。与此同时,医院端的转化效率也亟待提升。
数据显示,2021年全国约1600家三甲医院合计专利转化量仅1002件,平均每家医院不到1件。
**其次是同质化竞争引发的“内卷”。** 中国创新药研发存在靶点扎堆现象。例如,抗体药物大量集中在PD-1/PD-L1等靶点,CAR-T疗法则集中在CD19和BCMA。这种扎堆导致先发优势被快速摊薄,并引发了价格战。以PD-1药物为例,其价格随时间呈现明显下降趋势,企业利润空间被大幅压缩。

**支付机制的衔接不足同样制约创新药落地。** 《中国创新药械多元支付白皮书(2025)》显示,2024年创新药销售额中,**医保基金支付约占44%,个人支付占比约49%,而商业健康险仅贡献7.7%**。

北京市政协委员朱海鸾指出,基本医保、商业健康险等多种保障方式在功能定位、支付规则等方面存在衔接不足,影响了创新药规范落地和可及性提升。
**人才与资金的结构性短板亦不容忽视。** 中国医药工业协会报告显示,国内药企研发投入强度平均仅为**4.5%**,远低于跨国药企(MNC)**15%-20%** 的常规水平。
融资层面,2025年1至11月,全球医疗健康领域一级市场融资合计约586亿美元,而同期国内市场融资仅有约82亿美元,形成强烈反差。

3. 探寻“北京方案”:技术赋能与机制创新
面对挑战,北京正依托其独特的资源禀赋,探索破局路径。
**人工智能(AI)被视作缩短研发周期的关键工具。** 北京市政协委员郭田德认为,通过AI技术可以显著缩短药物研发周期。北京中医药大学的闫永红进一步指出,结合真实世界数据与人工智能,**有望将新药研发周期缩短至少三年**。
**在转化模式上,高校正进行机制创新。** 北京理工大学率先探索 **“先赋权后行权”** 模式,即学校先保留知识产权所有权,允许教师和企业使用成果进行市场化验证;待企业发展到一定规模后,学校再转让所有权并获取收益。
这套模式简化了审批流程,并降低了高校对国有资产流失的顾虑,即使创业失败,成果还可“二次赋权”。
**医院与企业的协同也在深化。** 北京大学第三医院通过举办科技成果推介会,集中呈现44项成果,并搭建医产学研协同平台。北京中医药大学房山医院则与驼人控股集团建立战略协作,旨在以临床需求为导向,打通“基础研究—临床应用—产业转化”的创新链条。

**针对支付难题,政策层面的优化已提上议程。** 朱海鸾委员建议,应完善顶层设计,加强医疗、医保、商保等政策的统筹衔接,并探索将创新药规范应用纳入医院绩效管理体系。
4. 从万亿规模到价值引领
北京医药健康产业站上万亿规模的新起点,其意义远超一个数字。它既是对过去政策引导、资源集聚和效率优势的肯定,也清晰地标示出未来的主攻方向:破解从技术到产品、从研发到商业化的系统性难题。
当AI加速药物发现,当转化机制不断疏通,当支付体系趋向协同,北京的产业优势才能从 **“成本与规模”** 转化为 **“创新与价值”** 的全球竞争力。从跟随到并跑,乃至在部分领域实现领跑,这条路径考验的不仅是科学家的智慧,更是整个产业生态的协同与韧性。
100 项与 北京理工大学 相关的药物交易
登录后查看更多信息
100 项与 北京理工大学 相关的转化医学
登录后查看更多信息
组织架构
使用我们的机构树数据加速您的研究。
登录
或

管线布局
2026年03月01日管线快照
管线布局中药物为当前组织机构及其子机构作为药物机构进行统计,早期临床1期并入临床1期,临床1/2期并入临床2期,临床2/3期并入临床3期
药物发现
6
12
临床前
登录后查看更多信息
当前项目
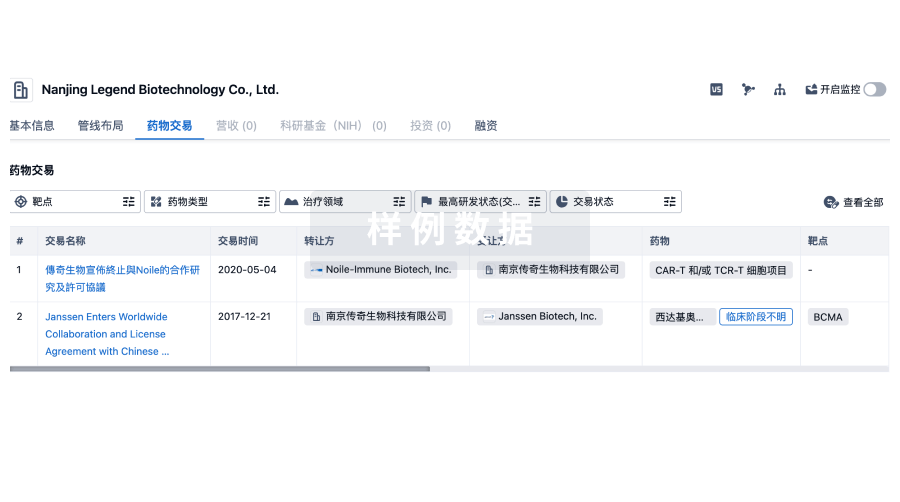
药物交易
使用我们的药物交易数据加速您的研究。
登录
或
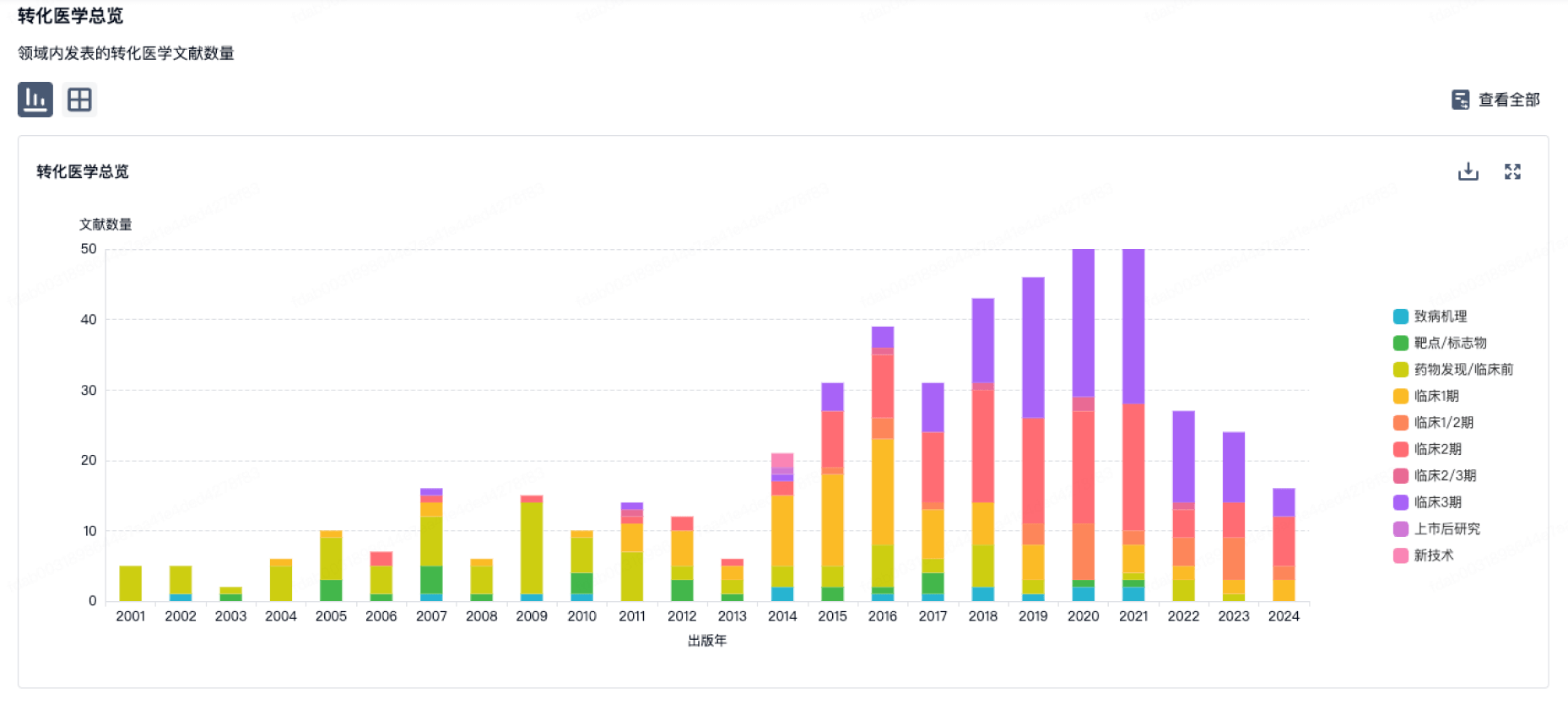
转化医学
使用我们的转化医学数据加速您的研究。
登录
或
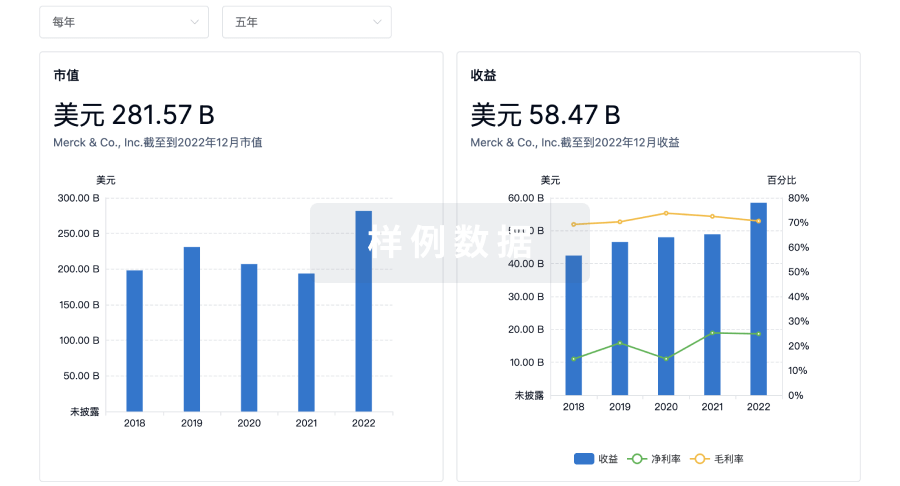
营收
使用 Synapse 探索超过 36 万个组织的财务状况。
登录
或
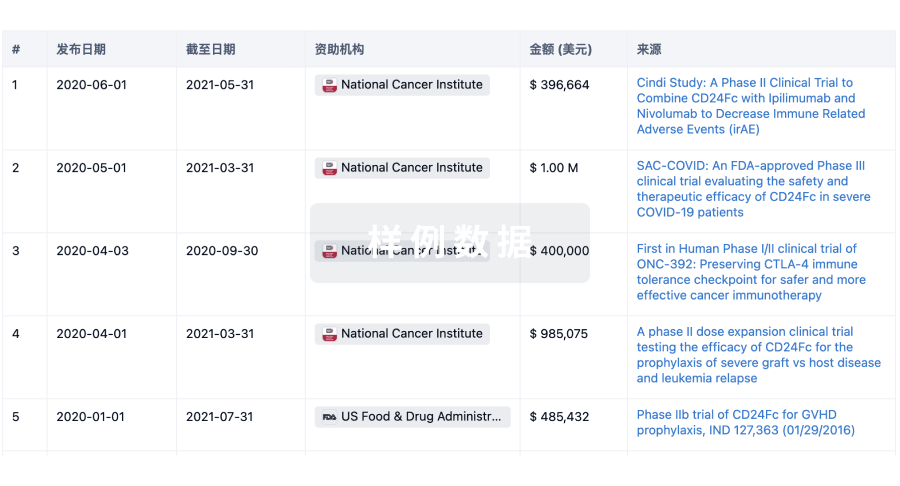
科研基金(NIH)
访问超过 200 万项资助和基金信息,以提升您的研究之旅。
登录
或
投资
深入了解从初创企业到成熟企业的最新公司投资动态。
登录
或
融资
发掘融资趋势以验证和推进您的投资机会。
登录
或
生物医药百科问答
全新生物医药AI Agent 覆盖科研全链路,让突破性发现快人一步
立即开始免费试用!
智慧芽新药情报库是智慧芽专为生命科学人士构建的基于AI的创新药情报平台,助您全方位提升您的研发与决策效率。
立即开始数据试用!
智慧芽新药库数据也通过智慧芽数据服务平台,以API或者数据包形式对外开放,助您更加充分利用智慧芽新药情报信息。
生物序列数据库
生物药研发创新
免费使用
化学结构数据库
小分子化药研发创新
免费使用
