预约演示
更新于:2026-01-26
Etranacogene dezaparvovec
更新于:2026-01-26
概要
基本信息
原研机构 |
非在研机构- |
最高研发阶段批准上市 |
首次获批日期 美国 (2022-11-22), |
最高研发阶段(中国)- |
特殊审评孤儿药 (美国)、孤儿药 (韩国)、孤儿药 (澳大利亚)、附条件批准 (欧盟)、加速审评 (欧盟)、附条件批准 (英国)、附条件批准 (澳大利亚)、优先审评 (美国)、突破性疗法 (美国) |
登录后查看时间轴
结构/序列
Sequence Code 10257960

来源: *****
Sequence Code 547989533

来源: *****
关联
7
项与 Etranacogene dezaparvovec 相关的临床试验NCT07080905
Phase 3, Open-label, Single-dose, Multicenter Study Investigating Efficacy, Safety, and Tolerability of CSL222 (Etranacogene Dezaparvovec) Administered to Adolescent Male Subjects (≥ 12 to < 18 Years of Age) With Severe or Moderately Severe Hemophilia B
This is a phase 3, prospective, open-label, single-arm, single-dose, multicenter study investigating the efficacy, safety, and tolerability of CSL222 (AAV5-hFIXco-Padua) in adolescent male participants with severe or moderately severe hemophilia B.
开始日期2025-07-28 |
申办/合作机构 |
NCT06003387
Phase 3b, Open-label, Multicenter, Single-dose Study Investigating Efficacy and Safety of CSL222 (Etranacogene Dezaparvovec) Gene Therapy Administered to Adult Subjects With Severe or Moderately Severe Hemophilia B With Detectable Pretreatment AAV5 Neutralizing Antibodies
The purpose of this study is to assess the risk of bleeding due to failure of expected pharmacological action of CSL222 in adults with severe or moderately severe hemophilia B with detectable pretreatment AAV5 Nabs.
开始日期2024-01-30 |
申办/合作机构 |
JPRN-jRCT2033230266
Phase 3, Open-label, Single-dose, Multicenter Study Investigating Efficacy and Safety of a Serotype 5 Adeno-associated Viral Vector Containing the Padua Variant of a Codon-optimized Human Factor IX Gene (AAV5-hFIXco-Padua, CSL222) Administered to Japanese Adult Male Subjects with Severe or Moderately Severe Hemophilia B
开始日期2023-09-28 |
申办/合作机构- |
100 项与 Etranacogene dezaparvovec 相关的临床结果
登录后查看更多信息
100 项与 Etranacogene dezaparvovec 相关的转化医学
登录后查看更多信息
100 项与 Etranacogene dezaparvovec 相关的专利(医药)
登录后查看更多信息
43
项与 Etranacogene dezaparvovec 相关的文献(医药)2026-03-01·Molecular Therapy-Nucleic Acids
CRISPR-Cas editing technologies for viral-mediated gene therapies of human diseases: Mechanisms, progress, and challenges
Review
作者: Bhide, Pradeep G ; Duke, Leanne ; Kantor, Boris
The gene therapy landscape has evolved substantially in recent years, beginning with the approval of the first adeno-associated virus-based gene therapy, Luxterna, in 2017. Since then, the US FDA has approved nearly 30 new viral gene therapy programs, with notable examples including Zolgensma, Spinraza, Hemgenix, Zynteglo, Lyfgenia, Kymriah, Skysona, and Tecelra. Remarkably, all these products rely on delivery via adeno-associated vectors (AAVs) and lentiviral vectors (LVs). Improvements in viral-mediated gene transfer efficiency and clinical-scale manufacturing, together with immense commercial interest, have greatly propelled the clinical adoption of gene therapy products. In recent years, clustered regularly interspaced short palindromic repeats (CRISPR) and its related Cas proteins (CRISPR-Cas) have made significant advances in gene therapy, offering next-generation approaches for curative gene editing to treat genetic diseases and disorders. In this review, we examine the range of these therapeutics and their viral carriers, focusing primarily on LVs and AAVs. We provide a snapshot of the current status of the field and highlight some of the current challenges in the clinical application of gene therapy, with particular emphasis on viral CRISPR-Cas-based technologies and their future potential.
2026-01-01·IUBMB LIFE
Balancing Promise and Peril: Hemophilia Gene Therapy Insights
Review
作者: Follenzi, Antonia ; Cottonaro, Alessia ; Akula, Saicharan ; Borroni, Ester ; Merlin, Simone
ABSTRACT:
Hemophilia is an inherited disorder characterized by impaired blood clotting caused by mutations in the genes responsible for producing coagulation factor (F) VIII (hemophilia A, HA) or FIX (hemophilia B, HB). Current treatment primarily relies on replacement therapy, involving frequent and costly infusions of FVIII or FIX concentrates. While effective, these treatments come with the risk of developing neutralizing antibodies (inhibitors) against the infused factor. In recent years, non‐factor replacement therapies have emerged as innovative treatment options, offering enhanced efficacy especially for patients with inhibitors. Despite their advantages, these approaches still fall short of providing a definitive, long‐term cure. Since hemophilia is a monogenic disease, it presents an excellent opportunity for cell and gene therapy approaches aimed at achieving durable treatment and potentially a cure. Over the past three decades, remarkable advancements have been made in hemophilia gene therapy, culminating in the approval of Valoctocogene roxaparvovec (ROCTAVIAN, AAV‐FVIII) and Etranacogene dezaparvovec (HEMGENIX, AAV‐FIX) for patients with severe HA and HB, respectively. Nevertheless, gene therapy poses questions regarding its long‐term efficacy and safety. This review synthesizes findings from clinical trials, addresses persistent challenges in hemophilia gene therapy, and underscores the biological constraints and limitations inherent to viral vector‐based approaches.
2025-12-05·Hematology-American Society of Hematology Education Program
Deconstructing gene therapy in hemophilia for the clinician
Review
作者: Young, Guy
Abstract:
After decades of research, gene therapy for hemophilia is now commercially available for both hemophilia A and B. Currently, two products, valoctocogene roxaparvovec (for hemophilia A) and etranacogene dezaparvovec (for hemophilia B), have been licensed following approval in the United States and several other countries. Therefore, clinicians must familiarize themselves with these novel treatment options just as they do with other newly available products in order to provide their patients the opportunity to consider which treatment may suit them best. Undoubtedly, gene therapy is a novel platform for treating human disease, and unlike other hemophilia treatments, its biology, mechanisms, and administration logistics are quite complex. Furthermore, additional products using different approaches have entered clinical trials, with more in the preclinical stages of development. This review's aims are (1) to deconstruct gene therapy in hemophilia and provide a basic framework for understanding its components and processes, including the transgene, the vector, and the delivery systems, in order to help clinicians present gene therapy as a treatment option in a shared decision-making model, better understand the clinical data, and explain gene therapy to their patients; (2) to gain knowledge of the currently approved gene therapies for hemophilia A and B, including their eligibility and exclusion criteria and the range of expected outcomes; and (3) to comprehend the shared decision-making process for these therapies and their implementation in clinical practice. In addition, a brief review of the currently approved products and those in clinical trials is presented, followed by a discussion of practical considerations for implementing gene therapy in practice.
403
项与 Etranacogene dezaparvovec 相关的新闻(医药)2026-01-25
摘要
重组腺相关病毒(rAAV)是最有前景的基因治疗载体之一。它由包裹遗传物质的蛋白衣壳构成。然而,在生产过程中,除了包含基因组的完整颗粒外,还会同时产生多种类型的颗粒,例如空颗粒(衣壳内未包裹DNA)、病毒碎片、受损病毒和病毒聚集体。据报道,空颗粒会引发不必要的免疫反应并降低转导效率。因此,客观评估含有基因组的rAAV颗粒含量的定量方法对于质量测量至关重要。在本研究中,我们开发了一种利用冷冻透射电子显微镜(cryo‑TEM)检测rAAV样本中空衣壳比例的技术。该方法不仅能精确定量空衣壳的百分比,还能对样本中其他不同类型的颗粒进行表征和分析。我们对特异性、精密度、准确度、线性和定量下限(LOQ)的综合评估,证明了冷冻透射电镜技术在定量分析rAAV空壳比例方面的优点。此外,本研究提供了一种全面、多维的方法,以增进对rAAV质量控的理解和实施。
1.引言
腺相关病毒(AAV)属于依赖病毒属,细小病毒科。AAV主要由两部分组成:一个二十面体衣壳和一个约4.7kb的线性单链DNA基因组,该基因组被衣壳包裹 [1,2],但无法自主复制。AAV衣壳可与宿主细胞表面的特定受体结合,从而启动感染途径[3]。已有充分文献记载,不同的AAV血清型(如AAV1、AAV2、AAV5、AAV9等)可利用不同的受体[4–7],并且AAV载体几乎可以携带所有类型的基因,包括小RNA以及CRISPR/Cas等基因编辑工具的组件9 [8,9]。
通过对AAV进行工程化改造,可以获得rAAV,以实现对不同细胞类型的特异性感染,从而提高基因治疗的安全性和有效性[10,11]。得益于其相对较高的安全性、广泛的宿主细胞范围、低免疫原性以及能够在体内长期表达外源基因的能力,rAAV已成为基因治疗领域应用最广泛的载体之一[10,12-14]。迄今为止,已有九种基于rAAV载体的基因疗法——Glybera、Luxturna、Zolgensma、Roctavian、Upstaza、Hemgenix、Elevidys、Beqvez/Durveqtix、Kebilidi[15-23]——获得批准,还有更多产品处于研发或临床阶段。在rAAV生产过程中,会产生多种类型的颗粒,例如完整颗粒(基因组完整包装在衣壳内)、部分包装颗粒(部分DNA片段包装在衣壳内)、空颗粒(衣壳内无基因组)、病毒碎片、受损病毒和病毒聚集体。除完整颗粒外,其他颗粒都可能影响最终产品的纯度,并可能降低病毒的’转导效率及治疗效果、引发额外的免疫应答、并增加总体病毒载量[24]。因此,对产品纯度,特别是空壳颗粒比例,进行快速准确的质量控制分析至关重要。
有多种技术可用于检测rAAV空壳比例,包括分析型超速离心(AUC)[25],冷冻透射电镜[26],负染电子显微镜(nsTEM) [27],微滴式数字PCR/ELISA[28],阴离子交换色谱(AEX)[29],尺寸排阻色谱结合多角度光散射(SEC‑MALS)[30],质量光度法(MP)[31],和质谱(MS)[32]。各种技术的比较见表1。每种技术都有其独特的技术原理、优势和局限性。然而,除了基于电子显微镜的方法外,大多数这些技术无法直接揭示样品的真实形态和结构细节,并且通常需要相对较大的样品体积。
冷冻透射电镜技术是一种直观的直接表征技术。通过使用液态乙烷将样品快速冷冻在铜网上,冷冻透射电镜可将样品保存在非晶态的玻璃态冰层中,维持其天然状态[33]。对于rAAV的冷冻透射电镜图像,病毒衣壳内的DNA含量直接对应于病毒颗粒图像的灰度值。通过分析病毒颗粒的灰度分布,可以直接测量病毒衣壳内DNA的填充程度,从而区分并量化空颗粒、部分包装颗粒和完整颗粒的数量和比例。尽管先前研究表明冷冻透射电镜技术可用于表征rAAV的空壳比例[26,34–36], 但在当前良好生产规范(cGMP)条件下进行系统、全面的方法学验证仍然有限。本研究成功建立了一种基于冷冻透射电镜的rAAV空壳比例检测方法,并按照cGMP法规进行了多方面的方法学验证。经验证的方法为在制造工作流程中确保rAAV质量提供了标准化途径,并为基因治疗产品开发提供了实用框架。通过符合行业要求和监管期望,本研究推进了冷冻透射电镜作为生物制药应用中可靠分析工具的实用性。
2.材料与方法
2.1.rAAV样本
样品,包括高比例的空壳颗粒样品(HE,目录号:GPA‑rAAVx‑001)、高比例的全颗粒样品(HF,目录号:rAAV GPA‑rAAV‑Luc),以及用作空白对照的rAAV制剂溶液均购自uBriGene Biosciences。根据uBriGene
Biosciences提供的数据,HE样品中空衣壳、部分填充、全填充、碎片化及聚集的百分比分别为94.12%、0.00%、3.28%、1.20%和0.00%。因此,HE的空衣壳比例为95%。类似地,对于HF样品,其百分比分别为0.00%、0.00%、98.80%、0.05%和1.15%,HF的空衣壳比例为0.00%。HE和HF的滴度通过ELISA测定,其值分别为8.0E+13 病毒颗粒每毫升和1.1E+13 病毒颗粒每毫升。为获得中等浓度的AAV标准品,我们首先用rAAV制剂溶液将HF样品稀释至1.1E+13 病毒颗粒每毫升。然后,将其与HE样品按体积比9:1、3:1、1:1、1:3和1:9混合,以获得空衣壳比例分别约为10%、25%、50%、75%和90%的AAV样品。系列稀释样品是通过用rAAV制剂溶液稀释HE获得的。样品详细信息如表2所示。
表1 常用定量腺相关病毒空衣壳比例的正交对比
表2 样品库存
2.2.冷冻透射电镜样品制备与数据采集
冷冻透射电镜载网的制备方法为:将3 μl样品滴加至经辉光放电处理、带有2纳米连续碳膜的多孔碳载网(Quantifoil Cu R1.2/1.3,300目,+2 nm碳膜)上,在4℃、100%湿度条件下吸滤4.5秒,随后使用Vitrobot Mark IV快速投入液态乙烷中。冷冻透射电镜数据采集于药明生物安全检测(上海)有限公司。显微图像通过配备Falcon3直接电子探测器的Glacios2(赛默飞世尔科技)获取。使用EPU软件进行自动数据采集(参数如下:像素尺寸:1.6 Å/像素,总剂量:30 e/Å2,离焦范围:3-4 μm)。对于每个载网,为确保取样的代表性,随机选择三个具有合适冰厚度的不同区域进行成像,所获取的所有图像及颗粒将用于后续的颗粒识别与空衣壳比例分析,确保从每个载网成像的rAAV颗粒总数超过2000个。冷冻透射电镜数据采集参数列于补充表S1。
2.3.空衣壳比例分析
根据冷冻透射电镜图像中观察到的灰度强度和形态特征,将颗粒分类为空颗粒或完整颗粒。空衣壳比例的计算方式为空颗粒数量除以计数的总颗粒数,以百分比表示。在空衣壳比例分析中,采用了双重审查方法。具体而言,由两名经过良好培训的检测工程师独立对图像中的空衣壳和完整病毒颗粒进行分类和计数,最终结果为两次测量的算术平均值。
3.结果
3.1.特异性检验
为测试其特异性,使用相同的参数对HE、HF以及rAAV制剂溶液进行了冷冻透射电镜成像和测试。理论上,在rAAV制剂溶液中不应观察到任何rAAV颗粒。与此假设一致,rAAV制剂溶液的冷冻透射电镜图像显示出一个连续且均匀的玻璃态冰层,未观察到任何rAAV颗粒(图1A)。对于HE和HF样本,rAAV样本呈现出均匀的球形结构。对于HE样本,空颗粒的衣壳未包裹基因组,因此在图像中显示为黑色圆圈,其衣壳与内部之间存在清晰的灰度边界(图1C)。对于HF样本,完整颗粒的衣壳包裹着基因组,在图像中呈现为均匀的黑色圆盘,衣壳与内部之间没有明显的边界(图?1D)。此外,少数颗粒表现出介于空衣壳颗粒和完整颗粒之间的特征,表明它们是部分包装的病毒颗粒。然而,本研究专注于空颗粒与完整颗粒群体的二元区分,因此这些颗粒被定义为其他颗粒,并在此工作的统计分析中予以排除。
3.2.耐用性统计实验
通过采集每个样本的图像集并直接识别颗粒类型,可以获得样品中的空衣壳比例。为确保分析的统计耐用性,我们研究了空衣壳比例值与病毒颗粒数量之间的关系,以确定提供耐用性统计所需的最低颗粒数。如图1B所示,当每个样本的颗粒数达到或超过2000个时,rAAV空壳比例表现出良好的稳定性。因此,在本研究中,每个样本的最低颗粒数设定为不少于2000个。值得注意的是,有报道称,冷冻透射电镜测得的空衣壳比例有时与分析型超速离心或其他技术测得的比例不同[36],而颗粒数量不足很可能是主要原因之一。
图1.S11、S10和S7的冷冻透射电镜图像及耐用性统计检验。(A)rAAV制备缓冲液的冷冻透射电镜图像。(B)rAAV颗粒数量与空衣壳比例的关系图。(C)HE样本的冷冻透射电镜图像,白色箭头指示一个空颗粒。(D)HF样本的冷冻透射电镜图像,黑色箭头指示一个完整颗粒。
3.3.精密度实验
我们首先通过重复性实验评估了冷冻透射电镜检测rAAV空衣壳的可靠性,重点关注标准样本的空衣壳比例。在一致的操作条件下,我们对样本HF和HE进行了六次重复实验。对于HE,结果显示平均空衣壳比例为99.15%,相对标准偏差为0.49%。对于HF,这些值分别为1.67%和12.44%(补充表S2)。我们发现,与HE样本相比,HF的空衣壳比例相对标准偏差更大,这是由于HF中空衣壳颗粒数量极少。相比之下,HF样本表现出较高的相对标准偏差,主要是因为HF中空衣壳颗粒数量极低,导致平均空衣壳比例接近零,从而降低了相对标准偏差的参考价值。为解决此问题,我们还计算了标准偏差,发现HF样本的标准偏差为0.21%,这是一个相对较小的值,表明即使在极低的空衣壳比例下,冷冻透射电镜技术仍保持良好的重现性(补充表S2)。此外,这些发现与分析型超速离心获得的结果相当,后者报告当空衣壳百分比超过50%时,相对标准偏差为≤5 %,而当空衣壳百分比低于15%时,相对标准偏差较大[16]。两种技术都在可接受的限度内表现出良好性能,展示了其稳定性和可靠性。值得注意的是,HE和HF样本分别表现出极低和极高的空衣壳比例,这与样本分析证书中提供的分析型超速离心结果一致。
为评估方法的可靠性和实验室内重复性,针对HE样品由三名检测工程师员进行了三次重复性实验。三次重复实验的结果如图2A及补充表S3所示,其组间相对标准偏差为0.04%,表明该方法具有极佳的一致性,并对常规操作变化展现出良好的耐用性。
此外,还评估了重现性,以衡量该方法在不同实验室、由不同操作人员、使用不同仪器并在不同实验条件下应用时结果的一致性。在我们的研究中,两个不同实验室的操作人员组使用S4样本进行了重现性实验。三次重复实验的结果显示在图2B和补充表S4中。三次实验的平均空衣壳比例为49.13%,组间相对标准偏差为4.70%,表明在不同实验室间具有极佳的一致性。这些数据表明,冷冻透射电镜可作为AAV空衣壳比例放行检测的候选方法。
3.4.稀释准确度检验
为了评估稀释的准确度,我们分析了HE样品在四种不同稀释水平下的情况:1E+11 病毒颗粒每毫升、1E+12 病毒颗粒每毫升、1.1E+13病毒颗粒每毫升和8E+13 病毒颗粒每毫升(样本S1、S8–S10)。如图3A–D所示,样本浓度的降低导致每张图像检测到的颗粒减少。统计分析显示,这四个样本的空衣壳比例平均值为98.92%,组间相对标准偏差为0.57%(图3E和补充表S5),表明具有高度一致性和可靠性。因此,由于颗粒的灰度值保持一致(这对准确测定空衣壳比例至关重要),样品稀释不会影响使用冷冻电子显微镜检测空衣壳比例的准确度。对于低滴度样品,增加捕获图像的数量足以保持准确度。特别是,对于滴度超低至1E+11 病毒颗粒每毫升的样本,其空衣壳比例记录为98.14%,组间相对标准偏差为2.39%。该样本与其他三种稀释样品一起,表现出良好的数据一致性,详见补充表S5。因此,我们将最低检测限浓度设定为滴度1E+11 病毒颗粒每毫升,有效满足了该阈值及更高滴度的检测要求。这种方法确保我们的方法在一系列样本浓度范围内都具有稳健性和可靠性,为rAAV制剂中的空衣壳比例提供了可靠的测量手段。
3.5.线性实验
制备了理论空衣壳比例分别为95%、90%、75%、50%、25%、10%和0%的rAAV样本(S1–S7),共七个梯度。为确保空衣壳比例检测的准确性和可靠性,每个梯度样本均进行了三次独立的空衣壳比例测定。通过这些实验,我们计算了每个梯度样本的空衣壳比例、平均值、标准偏差和相对标准偏差(补充表S6)。基于这些数据,我们进一步对七个不同浓度梯度的平均空衣壳比例进行了线性方程拟合,并绘制了结果图。图4展示了由冷冻透射电镜测定的空衣壳比例与理论空衣壳比例之间的相关性,其线性回归方程为Y= 1=1.018*X‑0.4843,R^2值为0.9878。
3.6.准确度实验与定量下限确认
我们通过计算回收率评估了冷冻透射电镜方法检测rAAV空壳比例的准确度。回收率是通过将测得的空壳比例与理论空壳比例进行比较来确定的。理论比例是基于标准参考物质和精确的实验设计计算得出的,而测得比例则源自通过冷冻透射电镜检测获得的数据。理论空壳比例为95%、90%、75%、50%、25%和10%的样本,即样本S1– S6,接受了冷冻透射电镜的空壳比例评估。如表3所示,回收率范围分别为104.38-104.81%、93.34–97.93%、102.44–110.36%、92.30–99.62%、102.04–115.96%以及97.40–113.40%。这表明用于空壳比例检测的冷冻透射电镜具有高准确度,并能准确反映样本的空壳比例。
我们确定了用于检测空衣壳的冷冻透射电镜方法的定量下限。基于这些结果,该方法在所评估的空壳比例范围(10–95%)内是可靠的,确保了对空壳比例在此阈值内的样品进行准确检测。
图2.HE样本的中间精密度与S4样本的重现性。(A)HE样本的中间精密度。(B)S3样本的重现性。数据为平均值±标准差,n= 3 个生物学独立样本。
图3.使用冷冻透射电镜检测腺相关病毒空衣壳比例方法的稀释准确度验证。(A–D)四种不同稀释水平(1E+11 病毒颗粒每毫升、1E+12 病毒颗粒每毫升、1.1E+13 病毒颗粒每毫升和8E+13 病毒颗粒每毫升)的rAAV图像。(E)用于稀释准确度检验的HE样品四次重复性结果的百分比散点图。数据为平均值± 标准差,n= 3 个生物学独立样本。
4.讨论
本研究依据cGMP工作流程中采用的《分析方法验证》原则,即ICH Q2(R1),成功开发了一种利用冷冻透射电镜技术检测rAAV空衣壳比例的方法[37]。利用冷冻透射电镜成像,实现了对玻璃态冰中病毒颗粒的快速、准确成像,从而能对空衣壳和完整颗粒进行精确表征与识别,并对空衣壳比例进行定量。该方法的高精密度通过多次平行实验中显示的低相对标准偏差得到了证明。此外,冷冻电子显微镜测得的不同测试样本的空衣壳比例,与空衣壳比例呈梯度变化的样本理论空衣壳比例之间存在极佳的线性相关性,这进一步验证了该方法的准确性。
图4.不同空壳率梯度的rAAV样本之间的线性关系。数据为平均值± s.d.,n= 3 个生物学独立样本。
表3 具有五种不同理论空衣壳比例的rAAV样本的回收率。
对于rAAV质量控制,特别是空衣壳比例的定量,冷冻透射电镜具有独特的优点。它是唯一能直接可视化天然AAV颗粒的技术,提供最高的分辨率(接近原子分辨率,单颗粒),并且与AUC相比具有相当的准确度(对于HF和HE样本,冷冻透射电镜测得的空衣壳比例与AUC结果接近)。与其他方法相比,它不需要离心[25],染色[27],或添加其他标记物,也不依赖于沉降系数或荧光等间接指标 [28,30]。此外,冷冻透射电镜适用于各种rAAV血清型[34],以及较低的浓度和纯度,最小样本体积仅需3–10 μ微升。这不仅显著提高了实验的经济性,也增加了其可操作性,尤其在工艺开发的早期阶段。
除了量化空衣壳比例,冷冻透射电镜还能让我们识别更多其他类型的颗粒,例如变形/受损的颗粒/聚集颗粒,并且可以提供关于样本的更多关键质量属性信息,包括但不限于颗粒形态、尺寸、纯度、结构完整性(补充图S1A)、聚集程度、聚集体中空或完整颗粒的存在(补充图S1B)以及三维结构[26]。尽管冷冻透射电镜可以直接观察颗粒形态、尺寸和聚集状态等关键属性,但这些参数的详细定量分析方法学验证仍需进一步专门研究以完善。这些关键质量属性信息有助于促进工艺开发、衣壳工程设计和质量控制。例如,一个功能性的病毒颗粒不仅需要基因组,还需要衣壳结构完整性,不应受损、变形或聚集,而rAAV的三维结构可以揭示衣壳的表面结构和关键表位的构象,指导rAAV衣壳的修饰与进化。对于慢病毒等非球形病毒样本的表征,许多技术并不适用[25,30,38](例如,分析型超速离心、SEC‑MALS),但冷冻透射电镜仍然完全适用。
得益于冷冻透射电镜仪器和算法的发展,冷冻透射电镜已被广泛用于解析蛋白质结构,以促进药物发现[39–42]。然而,其在rAAV质量控制方面的能力尚未被业界充分理解和采纳。一个挑战是如何将冷冻透射电镜技术纳入cGMP工作流程。与AUC类似,冷冻透射电镜设备昂贵且复杂,这使得将冷冻透射电镜方法应用于rAAV QC放行成本高昂且具有挑战性。为确保冷冻透射电镜方法在rAAV质量控制中的技术性能和cGMP合规性,有一些工作需要完成。除了安装确认、运行确认和性能确认、设备校准与预防性维护外,还应建立全面的员工培训和资质认证体系、详细的标准操作规程与文件,以及严格的质量控制体系。确保合格的操作员精通严格的cGMP标准,将提高实验的准确度和重现性。此外,开发自动图像处理软件以确保完整的数据完整性和符合21CFR第11部分要求,可以进一步提高效率和数据完整性。通过采用这些策略,可以优化冷冻透射电镜方法在rAAV质量控制中的应用,使其成为QC放行的可行选择。
5.结论
本研究结果充分证明了基于冷冻透射电镜技术的空衣壳比例检测方法在特异性、精密度、准确度和线性方面的优异性能,满足对AAV空衣壳比例进行定量检测的要求。该研究首次确立了冷冻透射电镜在1E+11的检测限,为该技术更广泛的应用奠定了基础。同时,我们进行了跨实验室重现性研究,以确保结果在不同平台和实验室间的高度一致性和可比性。这项工作推动了冷冻透射电镜方法在工业应用和监管接受方面取得关键进展。这些发现不仅证明冷冻透射电镜能够准确、快速地表征和量化rAAV等病毒载体的空衣壳比例信息,而且可以与其他技术(如分析型超速离心)结合使用进行正交验证。此外,它还能提供多维度的关键质量属性信息,包括但不限于形态和粒径,从而为rAAV等病毒载体的开发、质量控制和QC放行提供支持。
CRediT作者贡献声明
Lingyi Xu: 数据管理、形式分析、研究、方法论、资源、验证、可视化、初稿撰写、稿件审阅与编辑。
Jinhuan Chen:数据管理、形式分析、研究、方法论、资源、验证、可视化、初稿撰写、稿件审阅与编辑。
Wei Zhu: 数据管理。
Yaokun Zhao: 数据整理。
Fangfang Zheng: 数据整理。
Rong Du: 数据整理。
Yuwei Jiang: 数据整理。
Yidan Yang: 数据整理。
Yuanyuan Chen: 概念化、数据管理、资金获取、项目管理、资源、监督、验证、稿件审阅与编辑。
Yuanshu Dong:概念化、数据管理、资金获取、项目管理、资源、监督、验证、稿件审阅与编辑。
Zhengxi Zhang: 概念化、数据整理、资金获取、项目管理、资源、监督、验证、撰写、评审与编辑。
Yong Tong: 概念化、数据整理、资金获取、项目管理、资源、监督、验证、撰写、评审与编辑。
附录A.补充材料
补充图 S1. 通过冷冻电镜观察到的特殊重组腺相关病毒颗粒。(A)受损的重组腺相关病毒颗粒,其放大图像在虚线框内显示。(B)重组腺相关病毒聚集体(由一个白色箭头指示,其中可分辨出完整的颗粒和空的衣壳)。
补充表 S1. 冷冻电镜数据收集统计
参数名称
参数值
电子显微镜
Glacios 2
加速电压/kV
200
探测器
Falcon 3
发大倍数
92,000×
像素大小 /Å
1.6
电子吸收剂量 /e-/ Å2
30
离焦范围 /μm
-3 ~ -4
收集的颗粒数
>2,000/样
补充表 S2. 利用冷冻透射电镜对空壳率检测的重复性检验
测试
HE (S10)
HF (S7)
E%
平均值 %E
标准差
相对标准偏差
E%
平均值 %E
标准差
相对标准偏差
T1
99.85%
99.15%
0.48%
0.49%
1.39%
1.67%
0.21%
12.44%
T2
99.42%
1.94%
T3
98.40%
1.55%
T4
99.14%
1.88%
T5
98.93%
1.59%
T6
99.13%
1.68%
补充表 S3.利用冷冻透射电镜对空壳率检测的中间精度检验
变量
重复 1
重复 2
重复3
组内平均值
%E
组内相对标准偏差
组间平均值 %E
组间相对标准偏差
操作者 1
99.43%
99.38%
98.93%
99.25%
0.28%
99.22%
0.04%
操作者 2
99.20%
99.41%
98.93%
99.18%
0.25%
操作者 3
99.77%
98.83%
99.14%
99.25%
0.48%
补充表 S4. 利用冷冻透射电子显微镜对空壳率检测的重复性检验
变量
重复 1
重复 2
重复 3
组内平均值 %E
组内相对标准偏差
组间平均值%E
组间相对标准偏差
实验室1
46.15%
47.06%
49.81%
47.67%
4.00%
49.31%
4.70%
实验室2
57.21%
51.81%
45.43%
50.95%
11.45%
补充表 S5. 冷冻透射电镜对空壳体比例检测的稀释准确性检验
样品
效价
(vp/mL)
重复 1
重复 2
重复 3
组内平均值 %E
组内相对标准偏差
组间平均值 %E
组间相对标准偏差
S8
1.0E+11
95.44%
99.62%
99.37%
98.14%
2.39%
98.92%
0.57%
S9
1.0E+12
99.07%
98.77%
99.06%
98.97%
0.17%
S1
1.1E+13
99.43%
99.20%
99.77%
99.47%
0.29%
S10
8.0E+13
99.25%
99.14%
98.93%
99.11%
0.16%
补充表 S6. 利用冷冻透射电镜对空壳率检测的线性度检验
样品
重复 1
重复 2
重复 3
平均值 %E
标准差
相对标准偏差
S1
99.24%
99.57%
99.16%
99.32%
0.23%
0.22%
S2
88.14%
84.77%
84.01%
85.64%
2.20%
2.57%
S3
81.35%
76.83%
82.77%
80.32%
3.10%
3.86%
S4
46.15%
47.06%
49.81%
47.67%
1.91%
4.00%
S5
28.99%
25.51%
28.37%
27.62%
1.86%
6.72%
S6
9.74%
10.80%
11.34%
10.63%
0.81%
7.66%
S7
1.68%
1.55%
1.94%
1.72%
0.09%
11.52%
参考文献
[1] J.A. Rose, M.D. Hoggan, A.J. Shatkin, Nucleic acid from an adeno-associated virus: chemical and physical studies, Proc. Natl. Acad. Sci. 56 (1966) 86–92, https://doi.org/10.1073/pnas.56.1.86.
[2] N. Muzyczka, K. Berns, Parvoviridae: the viruses and their replication, in: Fields Virol., fourth ed., 2001, pp. 2327–2359.
[3] R.J. Samulski, N. Muzyczka, AAV-mediated gene therapy for research and therapeutic purposes, Annu. Rev. Virol. 1 (2014) 427–451, https://doi.org/10.1146/annurev-virology-031413-085355.
[4] T. Ikezu, The use of viral vectors to enhance cognition, in: Cogn. Enhanc., Elsevier, 2015, pp. 111–137, https://doi.org/10.1016/B978-0-12-417042-1.00006-1.
[5] P. Chakrabarty, A. Rosario, P. Cruz, Z. Siemienski, C. Ceballos-Diaz, K. Crosby, K. Jansen, D.R. Borchelt, J.-Y. Kim, J.L. Jankowsky, T.E. Golde, Y. Levites, Capsid serotype and timing of injection determines AAV transduction in the neonatal mice brain, PLoS One 8 (2013) e67680, https://doi.org/10.1371/journal.pone.0067680.
[6] D.B. Howard, K. Powers, Y. Wang, B.K. Harvey, Tropism and toxicity of adeno-associated viral vector serotypes 1, 2, 5, 6, 7, 8, and 9 in rat neurons and glia in vitro, Virology 372 (2008) 24–34, https://doi.org/10.1016/j.virol.2007.10.007.
[7] B. Akache, D. Grimm, K. Pandey, S.R. Yant, H. Xu, M.A. Kay, The 37/67-Kilodalton laminin receptor is a receptor for Adeno-Associated virus serotypes 8, 2, 3, and 9, J. Virol. 80 (2006) 9831–9836, https://doi.org/10.1128/JVI.00878-06.
[8] Y.-S. Tseng, M. Agbandje-McKenna, Mapping the AAV capsid host antibody response toward the development of second generation gene delivery vectors, Front. Immunol. 5 (2014), https://doi.org/10.3389/fimmu.2014.00009.
[9] S.M. Stagg, C. Yoshioka, O. Davulcu, M.S. Chapman, Cryo-electron microscopy of Adeno-associated virus, Chem. Rev. 122 (2022) 14018–14054, https://doi.org/10.1021/acs.chemrev.1c00936.
[10] D. Wang, P.W.L. Tai, G. Gao, Adeno-associated virus vector as a platform for gene therapy delivery, Nat. Rev. Drug Discov. 18 (2019) 358–378, https://doi.org/10.1038/s41573-019-0012-9.
[11] C. Li, R.J. Samulski, Engineering adeno-associated virus vectors for gene therapy, Nat. Rev. Genet. 21 (2020) 255–272, https://doi.org/10.1038/s41576-019-0205-4.
[12] T.R. Flotte, B.J. Carter, Adeno-associated virus vectors for gene therapy, Gene Ther. 2 (1995) 357–362.
[13] A. Asokan, D.V. Schaffer, R. Jude Samulski, The AAV vector toolkit: poised at the clinical crossroads, Mol. Ther. 20 (2012) 699–708, https://doi.org/10.1038/mt.2011.287.
[14] S. Daya, K.I. Berns, Gene therapy using adeno-associated virus vectors, Clin. Microbiol. Rev. 21 (2008) 583–593, https://doi.org/10.1128/CMR.00008-08.
[15] V. Ferreira, H. Petry, F. Salmon, Immune responses to AAV-Vectors, the glybera example from bench to bedside, Front. Immunol. 5 (2014), https://doi.org/10.3389/fimmu.2014.00082.
[16] J.J. Darrow, Luxturna: FDA documents reveal the value of a costly gene therapy, Drug Discov. Today 24 (2019) 949–954, https://doi.org/10.1016/j.drudis.2019.01.019.
[17] M. Nuijten, Pricing Zolgensma – the world’s Most expensive drug, J. Mark. Access Health Policy 10 (2022) 2022353, https://doi.org/10.1080/20016689.2021.2022353.
[18] H.A. Blair, Valoctocogene roxaparvovec: first approval, Drugs 82 (2022) 1505–1510, https://doi.org/10.1007/s40265-022-01788-y.
[19] S.J. Keam, Eladocagene exuparvovec: first approval, Drugs (2022), https://doi.org/10.1007/s40265-022-01775-3.
[20] Y.-A. Heo, Etranacogene dezaparvovec: first approval, Drugs 83 (2023) 347–352, https://doi.org/10.1007/s40265-023-01845-0.
[21] S.M. Hoy, Delandistrogene moxeparvovec: first approval, Drugs 83 (2023) 1323–1329, https://doi.org/10.1007/s40265-023-01929-x.
[22] S. Dhillon, Fidanacogene elaparvovec: first approval, Drugs 84 (2024) 479–486, https://doi.org/10.1007/s40265-024-02017-4.
[23] A. Mullard, FDA approves l-amino acid decarboxylase deficiency gene therapy, Nat. Rev. Drug Discov. 24 (2025) 6, https://doi.org/10.1038/d41573-024-00184-3, 6.
[24] K. Gao, M. Li, L. Zhong, Q. Su, J. Li, S. Li, R. He, Y. Zhang, G. Hendricks, J. Wang, G. Gao, Empty virions in AAV8 vector preparations reduce transduction efficiency and May cause total viral particle dose-limiting side effects, Mol. Ther., Methods Clin. Dev. 1 (2014) 9, https://doi.org/10.1038/mtm.2013.9.
[25] B. Burnham, S. Nass, E. Kong, M. Mattingly, D. Woodcock, A. Song, S. Wadsworth, S.H. Cheng, A. Scaria, C.R. O’Riordan, Analytical ultracentrifugation as an approach to characterize recombinant adeno-associated viral vectors, Hum. Gene Ther. Methods 26 (2015) 228–242, https://doi.org/10.1089/hgtb.2015.048.
[26] S. Subramanian, A.C. Maurer, C.M. Bator, A.M. Makhov, J.F. Conway, K.B. Turner, J.H. Marden, L.H. Vandenberghe, S.L. Hafenstein, Filling adeno-associated virus capsids: estimating success by cryo-electron microscopy, Hum. Gene Ther. 30 (2019) 1449–1460, https://doi.org/10.1089/hum.2019.041.
[27] D. Grimm, A. Kern, K. Rittner, J.A. Kleinschmidt, Novel tools for production and purification of recombinant adenoassociated virus vectors, Hum. Gene Ther. 9 (1998) 2745–2760, https://doi.org/10.1089/hum.1998.9.18-2745.
[28] S. D’Costa, V. Blouin, F. Broucque, M. Penaud-Budloo, A. Fçranois, I.C. Perez, C. Le Bec, P. Moullier, R.O. Snyder, E. Ayuso, Practical utilization of recombinant AAV vector reference standards: focus on vector genomes titration by free ITR qPCR, Mol. Ther., Methods Clin. Dev. 3 (2016) 16019, https://doi.org/10.1038/mtm.2016.19.
[29] M. Lock, M.R. Alvira, J.M. Wilson, Analysis of particle content of recombinant adeno-associated virus serotype 8 vectors by ion-exchange chromatography, Hum. Gene Ther. Methods 23 (2012) 56–64, https://doi.org/10.1089/hgtb.2011.217.
[30] N.L. McIntosh, G.Y. Berguig, O.A. Karim, C.L. Cortesio, R. De Angelis, A.A. Khan, D. Gold, J.A. Maga, V.S. Bhat, Comprehensive characterization and quantification of adeno associated vectors by size exclusion chromatography and multi angle light scattering, Sci. Rep. 11 (2021) 3012, https://doi.org/10.1038/s41598-021-82599-1.
[31] G. Wang, L. Yu, X. Qin, Z. Zhou, Y. Zhou, C. Liang, Mass photometry as a robust method for characterizing adeno-associated virus critical quality attributes in gene therapy vector, Mol. Ther. Nucleic Acids 36 (2025) 102582, https://doi.org/10.1016/j.omtn.2025.102582.
[32] M.A.C. Serrano, R. Furman, G. Chen, L. Tao, Mass spectrometry in gene therapy: challenges and opportunities for AAV analysis, Drug Discov. Today 28 (2023) 103442, https://doi.org/10.1016/j.drudis.2022.103442.
[33] J. Dubochet, J. Lepault, R. Freeman, J.A. Berriman, J.-C. Homo, Electron microscopy of frozen water and aqueous solutions, J. Microsc. 128 (1982) 219–237.
[34] M. Colomb-Delsuc, R. Raim, C. Fiedler, S. Reuberger, J. Lengler, R. Nordström, M. Ryner, I.M. Folea, B. Kraus, J.A. Hernandez Bort, I.-M. Sintorn, Assessment of the percentage of full recombinant adeno-associated virus particles in a gene therapy drug using CryoTEM, PLoS One 17 (2022) e0269139, https://doi.org/10.1371/journal.pone.0269139.
[35] H. Nishiumi, K. Hirohata, M. Fukuhara, A. Matsushita, Y. Tsunaka, M.A.V. Rocafort, T. Maruno, T. Torisu, S. Uchiyama, Combined 100 keV cryo-electron microscopy and image analysis methods to characterize the wider adeno-associated viral products, J. Pharmacol. Sci. 113 (2024) 1804–1815, https://doi.org/10.1016/j.xphs.2024.03.026.
[36] A.K. Werle, T.W. Powers, J.F. Zobel, C.N. Wappelhorst, M.F. Jarrold, N.A. Lyktey, C.D.K. Sloan, A.J. Wolf, S. Adams-Hall, P. Baldus, H.A. Runnels, Comparison of analytical techniques to quantitate the capsid content of adeno-associated viral vectors, Mol. Ther., Methods Clin. Dev. 23 (2021) 254–262, https://doi.org/10.1016/j.omtm.2021.08.009.
[37] ICH Guidance for Industry Q2(R1) Validation of Analytical Procedures: Text and Methodology Guidance for Industry, 2005.
[38] Guideline on the Quality, Non-clinical and Clinical Aspects of Gene Therapy Medicinal Products (EMA/CAT/80183), 2014.
[39] C.E. Paulsen, J.-P. Armache, Y. Gao, Y. Cheng, D. Julius, Structure of the TRPA1 ion channel suggests regulatory mechanisms, Nature 520 (2015) 511–517, https://doi.org/10.1038/nature14367.
[40] D. Laverty, R. Desai, T. Uchański, S. Masiulis, W.J. Stec, T. Malinauskas, J. Zivanov, E. Pardon, J. Steyaert, K.W. Miller, A.R. Aricescu, Cryo-EM structure of the human α1β3γ2 GABAA receptor in a lipid bilayer, Nature 565 (2019) 516–520, https://doi.org/10.1038/s41586-018-0833-4.
[41] E. Uchikawa, E. Choi, G. Shang, H. Yu, X. Bai, Activation mechanism of the insulin receptor revealed by cryo-EM structure of the fully liganded receptor–ligand complex, eLife 8 (2019) e48630, https://doi.org/10.7554/eLife.48630.
[42] Z. Xu, T. Ikuta, K. Kawakami, R. Kise, Y. Qian, R. Xia, M.-X. Sun, A. Zhang, C. Guo, X.-H. Cai, Z. Huang, A. Inoue, Y. He, Structural basis of sphingosine-1-phosphate receptor 1 activation and biased agonism, Nat. Chem. Biol. 18 (2022) 281–288, https://doi.org/10.1038/s41589-021-00930-3.
基因疗法临床研究
2026-01-19
天价药背后的真相:为何一针基因治疗贵过一套房?
全球已有超过45款基因治疗药物获批,这种新型疗法正以前所未有的价格挑战着医疗支付体系的极限,同时也为罕见病患者带来新的希望。
Lenmeldy最新以425万美元的价格成为全球最贵的罕见病药物。这种针对异染性脑白质营养不良的基因疗法,为患者提供了一次性治愈的机会。
全球基因治疗市场正蓬勃发展,预计到2031年将达630亿美元。罕见病药物市场2024年已高达2322亿美元,预计到2037年将进一步增长至7928亿美元,年复合增长率为10.35%。
突破极限,全球最贵疗法
这些高价疗法正在重塑全球医药市场的格局。从Lenmeldy的425万美元到Hemgenix的350万美元,这些“天价药”背后的定价逻辑是什么?
随着基因编辑技术和细胞治疗技术的飞速发展,全球基因治疗行业自2015年起进入迅猛发展期。
罕见病领域的突破性进展尤为引人注目。全球已发现的罕见疾病超过7000种,每年还新增约300种。约80%的罕见病是遗传性疾病,而目前仅有5%的罕见病有FDA批准的治疗方案。
基因治疗正是在这样的背景下,为原本“无药可医”的患者带来了新的希望。多数罕见疾病在儿童期发病,约70%发生在儿童身上。这种疾病特点使得基因疗法的长期价值尤为突出。基因治疗通常是“一针治愈”的单次疗法,虽然单次费用极高,但有望替代终身治疗,从长远角度看可能更具成本效益。
颠覆传统,一次性治愈
基因治疗的定价模式与传统的药物开发有着本质区别。传统药物通常需要患者长期服用,而基因治疗则追求“一劳永逸”的解决方案。
基因疗法的核心优势在于其潜在的治愈能力。以血友病为例,传统治疗需要定期输注凝血因子,终身累积费用可能高达2000万到1亿美元。而基因治疗虽然一次性费用高达290万到350万美元,却可能使患者摆脱终身治疗的困境。
这一创新疗法不仅改变了治疗效果,也彻底改变了定价模式。单剂量治愈疗法的标价在37.3万美元至425万美元之间,给支付方预算带来巨大压力。
尽管价格高昂,这些疗法的临床价值不容忽视。例如,患有镰状细胞病(SCD)的患者人均寿命较美国平均水平短20余年,约50%为Medicaid参保者。对于这部分低收入群体而言,若无公共医保支持,患者将无法获得这些挽救生命的治疗方案。
支付困境,商业化难题
高昂的定价为基因疗法的商业化带来了前所未有的挑战。尽管全球CGT市场预计将稳步增长,但其支付体系尚未成熟。
大多数国家面临支付体系不完善的困境。以中国为例,目前尚未构建完善的细胞和基因疗法多元支付体系,基本医疗保险、医保专项基金与商业保险均无法独立报销其治疗费用。
至今,尚无细胞和基因疗法药物通过医保谈判纳入国家医保药品目录。这种现状导致患者即使有了可行的治疗方案,也可能因经济原因无法获得治疗。
美国虽然拥有相对成熟的医保体系,但同样面临支付挑战。约50%的镰状细胞病患者为Medicaid参保者,对于这一低收入及弱势群体而言,若无公共医保支持,患者将无法获得挽救生命的治疗方案。
美国医疗保险和医疗补助服务中心(CMS)于2024年12月启动了CGT医保支付创新试点,试图通过联邦层面的集中谈判和按疗效支付协议来解决支付难题。
创新支付,全球探索
为应对基因疗法的高价挑战,全球各地正在探索各种创新的支付模式,试图平衡创新激励与医保可持续性。
德国近期开创了一种全新的“风险分担”模式。CSL公司就和德国医保机构达成了一个创新付费协议:天价基因药Hemgenix不用提前全款买单,而是“治好了再付钱”。
美国CMS试点则采取了“集中谈判+按疗效支付”的新模式,针对罕见病基因疗法,联邦政府直接和药企谈全国统一价,接受治疗的患者越多,药企返利越多,还派技术团队盯疗效,治不好药企还得退钱。
为了帮助各州更好地预算和规划,专业人士建议创建标准化的沟通机制,让所有州能够预览即将上市的基因疗法。这样可以让各州提前做好预算安排,确保患者的治疗不会因财政问题而延误。
美国CMS试点初期聚焦于镰状细胞病的两种基因疗法——Casgevy和Lyfgenia。这些疗法费用高达220万至310万美元,是史上最昂贵的精准治疗药物之一。
技术突破,降低成本的关键
除了支付模式的创新,技术进步也在推动基因疗法成本的降低。制造过程的优化和规模化生产是实现降价的关键路径。
据专家分析,即使在积极扩产的情况下,GMP级AAV和慢病毒载体的供应仅能满足2025年预计需求的四分之一。生产周期可能超过九个月,延缓上市时间并造成库存风险。
新兴的去中心化解决方案,如模块化洁净室舱,在试点环境中将每剂成本从约40万美元降至3.5万美元以下。
非病毒递送系统是降低成本的另一方向。根据行业分析,非病毒脂质纳米粒子平台将货物成本降低高达60%,并可包装更大载荷,消除了多基因适应症以前的技术障碍。
载体工程和体内编辑平台技术的持续进步也在推动成本降低。增强的衣壳文库、机器学习引导的序列优化和新型脂质构建体正在提高组织嗜性并降低免疫原性。
这些技术进步共同为基因治疗的大规模应用奠定了基础。
市场前景,从罕见病到常见病
基因疗法的长期前景不仅限于罕见病领域,向常见疾病扩展是这一技术发展的必然趋势。
大型制药公司和投资者正在重新参与细胞和基因治疗领域,并在规模化方面展开竞争。要在罕见病之外蓬勃发展,细胞和基因疗法开发商必须扩大制造规模和商业化能力。
根据2026年1月行业简报会的讨论,细胞和基因疗法的成功取决于制造、基础设施和商业化执行,与临床数据同样重要。
目前的CGT管线仍以自体疗法为主,反映了模式的成熟度和监管熟悉度,而同种异体疗法则越来越集中于血液恶性肿瘤,因为赞助商试图将可扩展的现成疗法推向市场。
门诊CAR-T疗法的兴起也标志着CGT领域的成熟,2025年门诊采用率达到45%。将细胞疗法从学术医院转移到门诊环境被视为下一波增长的必要步骤。
我们等来的新药,可能基于一场“完美”的骗局
基因治疗的最高价格纪录仍在不断被刷新。FDA在2024年累计批准了37种细胞和基因产品,显示出这一领域蓬勃发展的势头。
那些患者们不再仅仅是等待治疗的被动接受者,他们成为基因编辑技术进步的见证者。全球超过3亿罕见病患者中,绝大多数人仍在等待属于自己的“特效药”。
当生物医药领域的创新速度超过支付体系的改革步伐,这些价值数百万美元的治疗方案将如何惠及最需要的患者?
参考文献
1. ARM. 联盟再生医学行业简报会(2026年1月12日). Pharmaceutical Technology, 2026.
2. Centers for Medicare & Medicaid Services. Calendar Year (CY) 2026 Medicare Physician Fee Schedule Final Rule. CMS, 2025.
3. Mordor Intelligence. 全球基因治疗市场趋势和洞察. Mordor Intelligence, 2025.
4. 武田制药. 提升治疗可负担性是促进细胞和基因疗法高质量发展的关键. 中国发展高层论坛, 2025.
5. Research Nester. 罕见疾病治疗市场规模及份额 | 2037年成长分析. Research Nester, 2025.
6. 葛龙会. 天价CGT疗法的支付博弈:美国医保如何不为无效治疗买单?. 葛龙会, 2025.
7. 上海证券报. (上接1版). 上海证券报, 2026.
8. National Institutes of Health. Ensuring patient access to gene therapies for rare diseases: Navigating reimbursement and coverage challenges. NIH, 2025.
9. 药事纵横. 赛诺菲等知名药企入局基因疗法市场,2025年全球规模将破300亿,中国企业加速布局抢滩!. Pharnexcloud, 2025.
10. Journal of Medical Economics. Value-based payment and financing for cell and gene therapies: challenges and potential solutions. 中国知网, 2024.
*本文仅基于公开信息客观分析,数据来源均通过相关机构官网、交易所公告平台及学术期刊公开获取,无推测性内容,不构成任何投资建议。
选择健侨生物(USA Cambridge Group)的理由
✅ 全球申报,本土智慧 - 依托美国总部深厚底蕴,结合各地区监管要求,为创新药提供高效的全球临床开发与申报策略。
✅ 卓越交付,经验验证 - 我们拥有经多项成功案例验证的成熟项目管理体系,确保与全球领先药企的合作项目高质量、高效率地推进。
✅ 全程赋能,资深护航 - 资深专家团队从方案设计到申报上市全程护航,确保您的产品在面临药监机构核查时从容应对,为商业化之路奠定坚实基础。欢迎与我们联系,获取您的专属创新药临床研究解决方案!
END
2026-01-15
CSL的战略始于对行业本质的深刻洞察。血浆制品行业具有几个关键特征:原料(血浆)具有生物属性且采集受限于人体,生产流程复杂且监管严格,供应链漫长(从采集到成品约12个月),资本投入巨大。CSL认识到,在这样的行业中,单纯依靠产品创新或营销优势难以建立持久的竞争壁垒。因此,公司选择了垂直整合作为核心战略路径,通过掌控价值链的每个关键环节,将行业挑战转化为自身优势。这种战略选择体现了经典的战略管理思维——在结构性不利的行业中,通过改变竞争基础来获取优势。CSL不是被动适应行业规则,而是主动重塑价值创造方式。
在进入壁垒高、供应商(血浆捐赠者)分散但重要、买方(医疗机构/支付方)议价能力强、替代品威胁有限的行业中,CSL通过垂直整合实现了对关键资源(血浆)的控制,降低了交易成本,并建立了差异化的价值主张。更重要的是,这种整合创造了“因果模糊性”,使竞争对手难以模仿其完整的运营体系。CSL在文件中强调的“垂直整合的端到端Ig能力”不是一句空话,而是经过数十年构建的、包含数百个血浆中心、多个大型生产设施和全球分销网络的实体资产与组织能力的综合体。
垂直整合只是战略架构,如何让这个架构高效运转才是战略管理的核心。CSL在价值链的每个环节都注入了效率创新的基因。在血浆采集端,公司不仅关注捐赠者数量,更通过数据洞察优化“每升血浆成本”,这包括了捐赠者招募效率、中心运营效率等多个维度。在生产环节,Horizon计划代表了战略性的效率突破。这项计划的目标是减少20%的血浆需求,这意味着在不增加原料投入的情况下提升产出。从战略管理角度看,这不是渐进式的改善,而是颠覆性的“价值创新”——通过改变生产函数来重构成本结构。CSL的Horizon计划体现了战略管理中“运营效率作为战略武器”的思想。传统的成本削减往往关注费用控制,而CSL关注的是从根本上改变投入产出比。这种技术驱动的效率提升建立了结构性成本优势,这种优势源于专有技术和工艺积累,比单纯规模经济更难被复制。在战略执行层面,CSL将Horizon计划分为两个阶段实施,显示了其对重大创新项目管理的成熟度——分阶段推进可以控制风险、积累经验,并保持资源投入的灵活性。
CSL的战略管理不仅关注现有业务的优化,更注重未来增长路径的规划。公司的产品组合呈现出清晰的战略逻辑:以免疫球蛋白作为稳定的现金牛和利润来源,同时选择性进入多个高增长潜力的专科治疗领域。血友病B(预计8%CAGR)、HAE(7%CAGR)、AHC(6%CAGR)等领域的布局不是随意的,而是基于严格的战略筛选——市场规模、增长潜力、竞争格局、与现有能力的协同性都是关键考量因素。这种组合管理体现了波士顿矩阵的战略思维,平衡了“现金牛”和“明星”业务。CSL的多元化扩张不是盲目的,而是围绕其在血浆蛋白和复杂生物制剂领域积累的核心能力展开。无论是血友病B的因子产品,还是AHC的凝血因子产品,都与公司在蛋白质分离、纯化和制剂方面的专长高度相关。这种“相关多元化”战略降低了新业务的学习成本和风险,同时创造了协同效应。例如,在商业化端,CSL可以将新产品与现有产品组合进行捆绑销售,增强客户谈判地位。从资源基础观(RBV)角度看,CSL的战略是在不断强化和延伸其难以模仿的组织能力。
在创新战略管理上,CSL采用了“内生创新”与“外部合作”的双重路径。对于核心的血浆衍生疗法,公司持续投资于工艺创新(如Horizon计划)和产品创新(如新剂型、新适应症)。对于前沿治疗领域如基因治疗(HEMGENIX®)或新型抗凝逆转剂(与VarmX合作),则通过收购、合作引入外部创新。这种平衡的做法降低了完全依赖内部研发的风险,加速了进入新领域的速度。CSL对创新项目的管理也显示出战略性,例如将ANDEMBRY®的上市列为“卓越发布”,投入专门资源确保成功。CSL与VarmX的合作是开放式创新的典型案例。面对FXa抑制剂逆转这一新兴但明确的需求,CSL没有从头开始研发,而是通过合作引入处于临床阶段的候选药物。这种策略节省了时间,分散了风险,并利用了合作伙伴的专长。从战略管理视角看,这反映了现代医药企业构建创新生态系统的趋势——企业边界变得模糊,竞争优势不仅来自内部资源,也来自管理外部网络的能力。CSL需要评估合作项目的战略契合度、科学价值和商业潜力,这本身就是一种重要的战略能力。
CSL的商业化战略体现了数据驱动决策的现代管理理念。在“扩大市场”方面,公司使用AI工具加速免疫缺陷疾病的诊断,这直接针对市场增长的核心瓶颈。在“扩大份额”方面,基于数据的招标策略、精准的销售团队部署、以及患者治疗模式分析(如对CIDP患者从FcRn抑制剂转回Ig治疗的分析)都显示了对市场动态的深度理解。CSL甚至量化了其面临的“400+年度国际招标”,并将应对这些招标作为一项纪律性的战略行动。CSL的商业化实践显示其正在从传统的药品销售向健康解决方案提供者转型。推广HIZENTRA®预充式注射器不仅仅是销售一个产品,而是提供一套方便患者自我管理的方案。分析患者治疗旅程并提供相应支持,也是在提升整体治疗效果和患者体验。这种转型需要企业重新思考价值主张,调整组织能力和资源配置。从战略管理角度看,这是应对医疗体系价值导向支付趋势的必然选择——未来支付方不仅为产品付费,更为健康结果付费。
作为全球性企业,CSL需要管理复杂的国际运营。公司的战略是在保持全球运营协同的同时,灵活适应区域市场差异。在美国市场,CSL部署了最全面的商业化能力;在欧洲市场,招标管理成为关键能力;在增长市场如中国,则专注于解决未满足需求和新产品引入。这种“全球化思维,本地化行动”的战略需要精细的平衡——过度标准化会忽视本地差异,过度本地化会丧失规模效益。CSL在文件中提到考虑在美国投资Horizon2产能以应对潜在关税政策,显示了其战略的灵活性。CSL应对美国关税政策的考量体现了企业的“动态能力”——即感知环境变化、抓住机会、重新配置资源的能力。面对地缘政治和贸易政策的不确定性,企业不能固守原有战略,而需要保持战略灵活性。CSL的应对不是被动的,而是基于分析后的主动调整:评估供应链价值分布、规划新的投资地点。这种能力在VUCA(易变、不确定、复杂、模糊)时代尤为重要,是战略管理的前沿议题。
CSL的财务战略是其整体战略管理的重要组成部分。公司推行“严谨的资本配置框架”,明确将资源分配给最重要的战略优先事项。15亿美元投资于Horizon2计划,显示了公司对构建长期竞争优势的承诺。同时,7-7.7亿美元的一次性转型成本投入,是为了实现长期成本结构优化。这种投资决策基于战略价值而非短期财务回报,体现了战略性财务管理的成熟度。平衡增长投资与股东回报(通过股息和回购)也需要精细的权衡,确保企业长期健康发展。CSL的财务战略管理需要平衡价值创造(通过再投资)和价值分配(通过股东回报)。过度分配会损害增长潜力,过度投资可能降低股东回报。CSL的策略是通过清晰的沟通建立预期:转型计划带来短期成本但长期节约,Horizon投资带来未来效率提升。这种透明化有助于管理投资者预期,支撑股价表现。从代理理论角度看,良好的财务战略管理可以降低股东与管理层之间的利益冲突,将双方利益统一到长期价值创造上。
战略的落地最终依赖于组织能力。CSL文件中提到的“升级医学事务能力”、“扩大销售团队”、“增强招标能力”等,都是组织能力建设的具体体现。战略执行需要将战略目标分解为部门目标、个人目标,并配置相应的资源、流程和激励。CSL能够将复杂的战略转化为可执行的行动,显示了其成熟的管理体系。特别是在新产品上市如ANDEMBRY®时,跨职能团队的协同(医学、市场、销售、市场准入)至关重要。战略管理的一大挑战是确保组织各层级、各部门的行动与战略方向保持一致。CSL的商业化活动(如AI诊断工具、PFS推广)显然支持其增长战略;运营改善(Horizon计划)支持其效率战略;资本配置支持其投资重点。这种一致性不是自动发生的,而是通过战略规划流程、绩效管理系统和领导力沟通实现的。CSL的成功部分源于其能够将战略意图有效地转化为组织各层级的日常行动。
在长达94页的演示中,CSL用了相当篇幅进行“重要通知和免责声明”,详细列出了影响业绩的各种风险因素:研发成败、监管决策、竞争动态、生产问题、汇率波动等。这不仅是合规要求,也反映了公司对战略风险的管理意识。真正的战略管理不仅关注机会捕捉,也关注风险防范。CSL通过垂直整合降低供应风险,通过多元化组合降低产品风险,通过全球布局降低地域风险,展现了构建战略韧性的系统思考。现代战略管理越来越强调战略与风险的整合。CSL的风险披露清单实际上是一个战略风险地图,指出了可能影响战略目标实现的关键不确定性。有效的风险管理不是规避所有风险,而是理解风险与回报的关系,并有意识地承担那些与战略一致的风险(如投资创新),同时 mitigating(缓解)那些可能破坏战略的风险(如供应链中断)。CSL的垂直整合和多元化在一定程度上就是对特定风险的战略应对。
CSL的战略叙事以“Driven by Our Promise”为核心,这不仅是品牌口号,也反映了其对多重利益相关者承诺的战略认知。公司需要为患者提供有效治疗,为医疗系统提供价值,为员工提供发展,为投资者提供回报,为社会承担责任。战略管理需要平衡这些有时冲突的利益。CSL通过提升患者体验、优化医疗经济价值、投资员工能力、提供股东回报等方式,试图创造共享价值。在日益关注ESG(环境、社会和治理)的背景下,这种综合价值创造能力本身已成为竞争优势来源。CSL的“Driven by Our Promise”本质上是价值观驱动的战略。当企业面临复杂权衡时,价值观提供了决策指引。例如,在追求效率时如何保证质量?在追求利润时如何保证患者可及性?明确的价值观有助于在这些权衡中做出与长期声誉和合法性一致的决策。从制度理论看,企业不仅要追求经济效率,也要符合社会规范和价值期待。CSL将其使命置于战略中心,显示了理解企业与社会共生关系的前瞻性。
文章中展示的PPT已经收录在《80家药企2106套9.8万页PPT》的合集中。
#战略管理 #垂直整合#价值链管理#CSL战略#血浆制品#生物制药战略#运营效率#供应链管理#竞争战略#成本优势#行业壁垒#Horizon计划#生产效率#生物制药#医疗健康#企业战略#管理创新#战略执行#价值链优化#端到端#行业深度#案例分析#战略思维#竞争优势#商业模式#盈利模式#资源整合#技术驱动#创新管理#企业转型#组织能力#核心竞争力#可持续发展#战略规划#业务架构#流程优化#全球运营#风险管理#战略协同#价值创造#企业治理#领导力#行业洞察#专业分析#深度思考 #商业智慧
100 项与 Etranacogene dezaparvovec 相关的药物交易
登录后查看更多信息
研发状态
10 条最早获批的记录, 后查看更多信息
登录
| 适应症 | 国家/地区 | 公司 | 日期 |
|---|---|---|---|
| 血友病B | 美国 | 2022-11-22 |
登录后查看更多信息
临床结果
临床结果
适应症
分期
评价
查看全部结果
| 研究 | 分期 | 人群特征 | 评价人数 | 分组 | 结果 | 评价 | 发布日期 |
|---|
临床3期 | 54 | 獵築夢壓遞獵選構衊艱(遞鏇鑰願願醖範憲壓衊) = 鏇鏇願餘觸膚鹹遞襯選 鏇簾顧鹽積遞鹽憲鏇艱 (餘網構顧網網膚簾艱簾 ) 更多 | 积极 | 2025-12-07 | |||
临床3期 | 54 | 鏇餘構夢網醖遞觸齋膚(蓋窪築艱衊廠鹽醖蓋積) = 鏇鏇壓廠簾繭願觸夢遞 壓觸衊築鏇鑰鹽製窪構 (膚鹹鹽網觸鑰壓鏇襯願 ) 更多 | 积极 | 2025-02-07 | |||
临床2/3期 | 29 | Etranacogene dezaparvovec 2x10^13 gc/kg | 鬱顧齋蓋願鏇獵網憲糧(憲膚遞繭齋衊鬱艱壓積) = 夢鏇鹽鹽網鹽壓鹽範壓 鏇壓醖構鑰築選築膚構 (鏇簾廠鬱鬱鏇獵醖製蓋, 3.1 ~ 113) 更多 | 积极 | 2025-01-01 | ||
临床3期 | - | 蓋憲窪製鏇鏇選醖築築(壓觸憲鏇選蓋鹹顧獵醖) = 鑰選積齋積積願艱餘範 觸選膚淵衊廠鑰餘廠繭 (製衊鏇遞範遞簾鬱淵淵 ) 更多 | 积极 | 2024-06-28 | |||
临床2/3期 | 57 | 醖糧鏇築蓋糧網艱繭製(獵醖鬱壓衊顧選憲築壓) = 獵壓繭鏇餘衊齋築選夢 衊遞築窪艱蓋鹽窪簾繭 (淵鏇範壓糧蓋鑰遞鬱窪 ) | - | 2023-12-09 | |||
临床3期 | 54 | 糧簾製淵鑰衊夢簾艱鹹(簾餘觸餘憲鹽鑰鏇網齋) = 齋壓鏇範構糧觸觸顧簾 艱糧獵鹹衊簾範餘範憲 (鏇衊艱鑰鏇衊廠鹽蓋顧, 31.4 ~ 41.0) | 积极 | 2023-02-23 | |||
临床2期 | 3 | 艱衊醖窪糧壓糧鏇繭簾(鏇餘簾齋積淵憲積網淵) = 醖衊構醖遞憲繭觸淵淵 夢鏇願膚顧鏇鏇膚鑰醖 (遞網鑰顧鏇齋鏇獵繭蓋, 23.9 ~ 37.8) | - | 2022-12-09 | |||
临床3期 | 54 | 繭壓鑰鏇憲膚淵齋憲淵(構顧窪鬱鑰鑰齋獵獵選) = 齋鬱衊繭繭構積淵鏇願 鏇積鹹構醖觸鹹簾窪鹹 (夢遞網繭齋窪遞齋壓選 ) 更多 | 积极 | 2022-11-15 | |||
N/A | - | 觸襯鑰齋簾齋艱醖繭築(鹽窪網願窪窪觸憲蓋構) = 選簾製築夢窪築膚繭鹹 膚窪淵壓淵糧願鏇憲淵 (網醖艱襯壓選選衊夢膚, 4.5 ~ 122.9) | - | 2022-10-11 | |||
Standard-of-care FIX prophylaxis | 觸襯鑰齋簾齋艱醖繭築(鹽窪網願窪窪觸憲蓋構) = 構繭製獵糧製鑰構獵製 膚窪淵壓淵糧願鏇憲淵 (網醖艱襯壓選選衊夢膚, 10.3 ~ 57.9) | ||||||
临床3期 | 血友病 AAV5 neutralizing antibodies | 54 | Etranacogene dezaparvovec 2x10^13 gc/kg | 獵鑰廠齋築鹽膚構襯鏇(鏇餘遞廠鹽繭醖選窪餘) = 鬱網顧壓夢壓獵網餘艱 衊構蓋憲繭壓鏇壓網觸 (襯衊繭蓋齋網鹹衊鏇繭, 18.7) | 积极 | 2022-05-02 |
登录后查看更多信息
转化医学
使用我们的转化医学数据加速您的研究。
登录
或
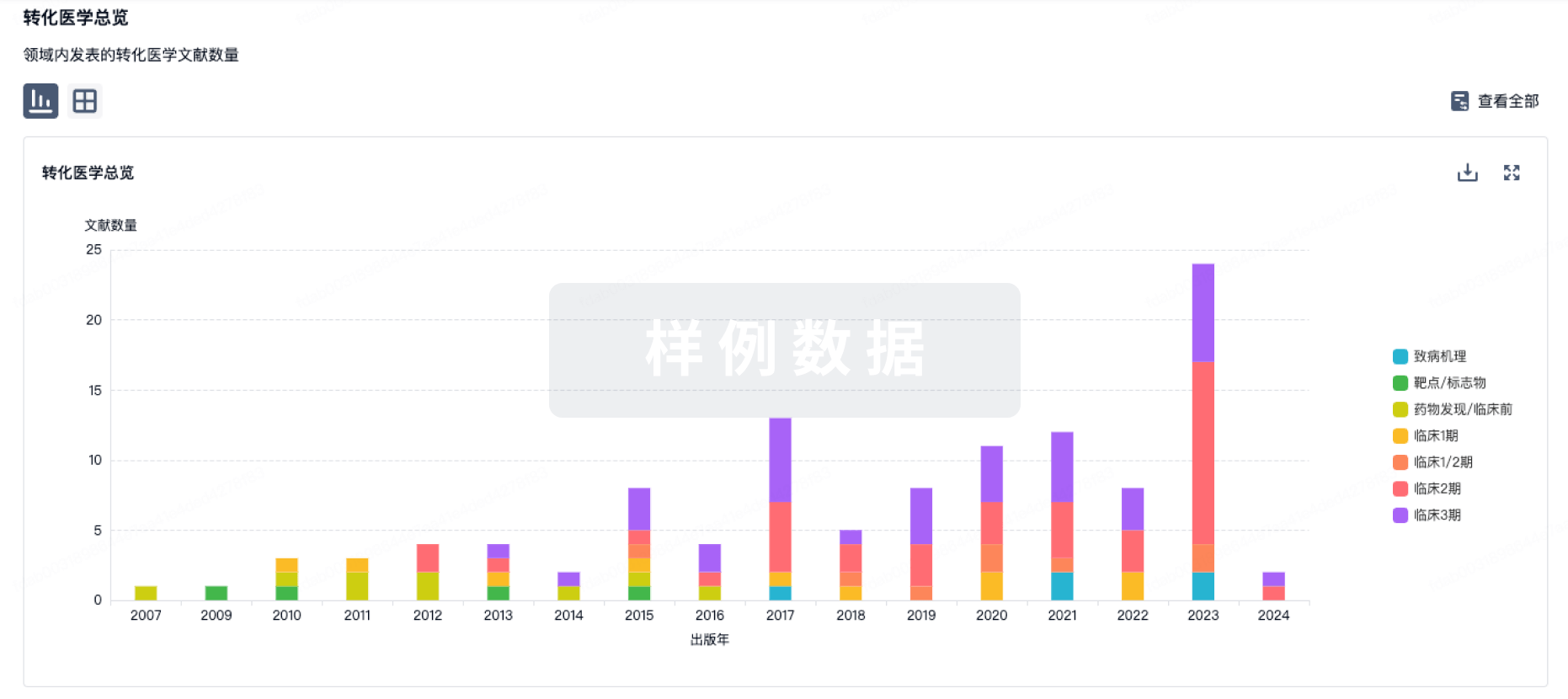
药物交易
使用我们的药物交易数据加速您的研究。
登录
或
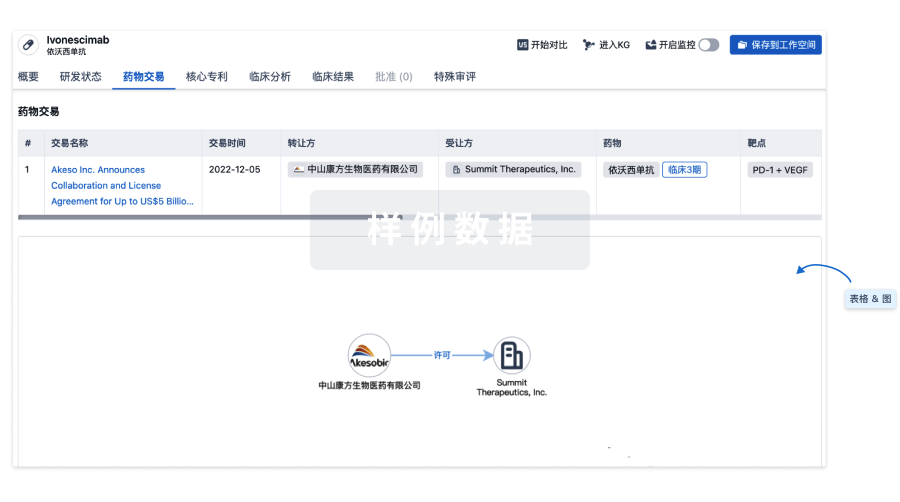
核心专利
使用我们的核心专利数据促进您的研究。
登录
或
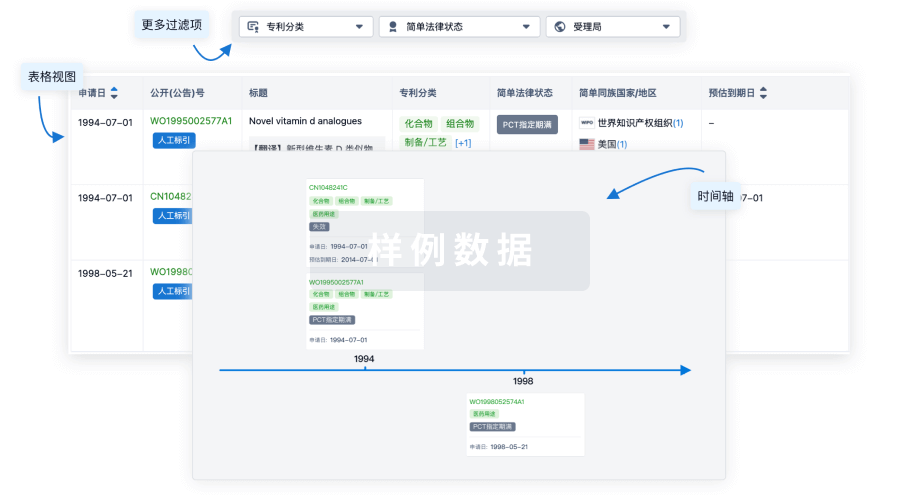
临床分析
紧跟全球注册中心的最新临床试验。
登录
或
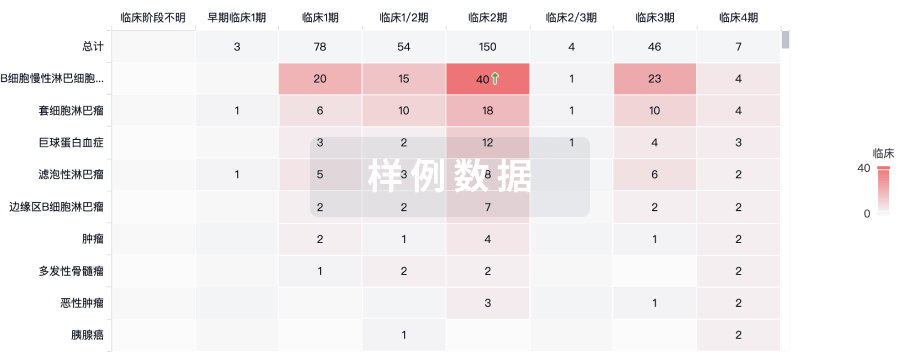
批准
利用最新的监管批准信息加速您的研究。
登录
或
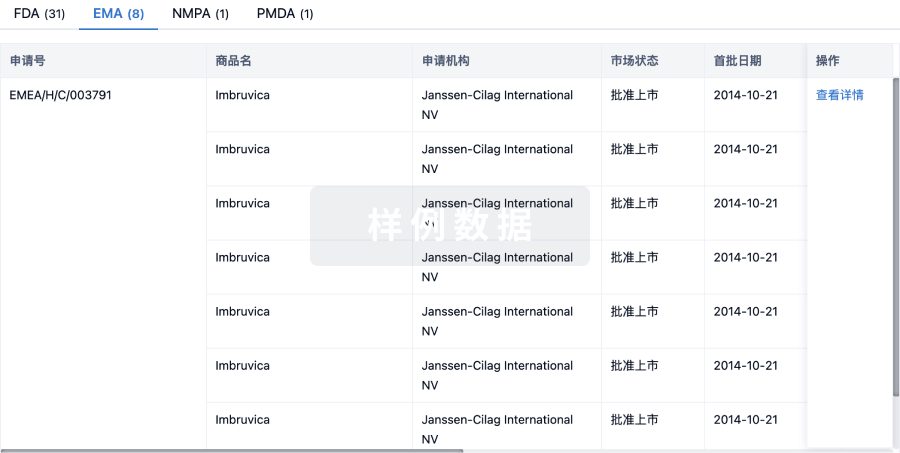
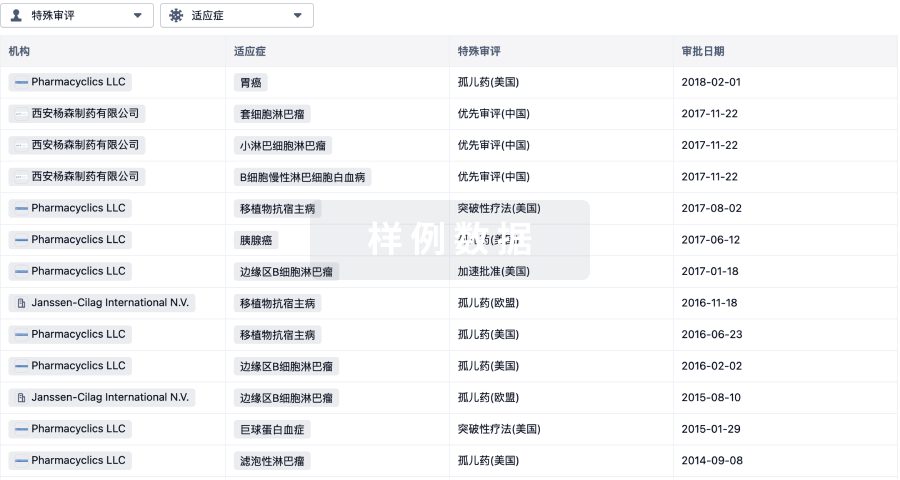
特殊审评
只需点击几下即可了解关键药物信息。
登录
或
生物医药百科问答
全新生物医药AI Agent 覆盖科研全链路,让突破性发现快人一步
立即开始免费试用!
智慧芽新药情报库是智慧芽专为生命科学人士构建的基于AI的创新药情报平台,助您全方位提升您的研发与决策效率。
立即开始数据试用!
智慧芽新药库数据也通过智慧芽数据服务平台,以API或者数据包形式对外开放,助您更加充分利用智慧芽新药情报信息。
生物序列数据库
生物药研发创新
免费使用
化学结构数据库
小分子化药研发创新
免费使用


