预约演示
更新于:2026-02-27
Nicotinamide riboside/Pterostilbene
更新于:2026-02-27
概要
基本信息
非在研机构- |
最高研发阶段临床2期 |
首次获批日期- |
最高研发阶段(中国)- |
特殊审评- |
登录后查看时间轴
结构/序列
分子式C11H15N2O5 |
InChIKeyJLEBZPBDRKPWTD-TURQNECASA-O |
CAS号1341-23-7 |
查看全部结构式(2)
关联
73
项与 Nicotinamide riboside/Pterostilbene 相关的临床试验ChiCTR2600116332
The improvement and impact of exercise rehabilitation on fatigue in patients with hypertrophic cardiomyopathy after the application of Mavacamten
开始日期2026-01-10 |
申办/合作机构 |
ChiCTR2500113830
Assessing the Efficacy and Safety of External Tibetan Medicine in the Treatment of Motor Pain After Knee Arthroplasty
开始日期2025-12-01 |
申办/合作机构 |
ChiCTR2500112475
Effects and EEG mechanisms of priming Intermittent Theta Burst Stimulation with High-Definition Transcranial Direct Current Stimulation on Cognitive Function in Depression
开始日期2025-10-30 |
申办/合作机构 |
100 项与 Nicotinamide riboside/Pterostilbene 相关的临床结果
登录后查看更多信息
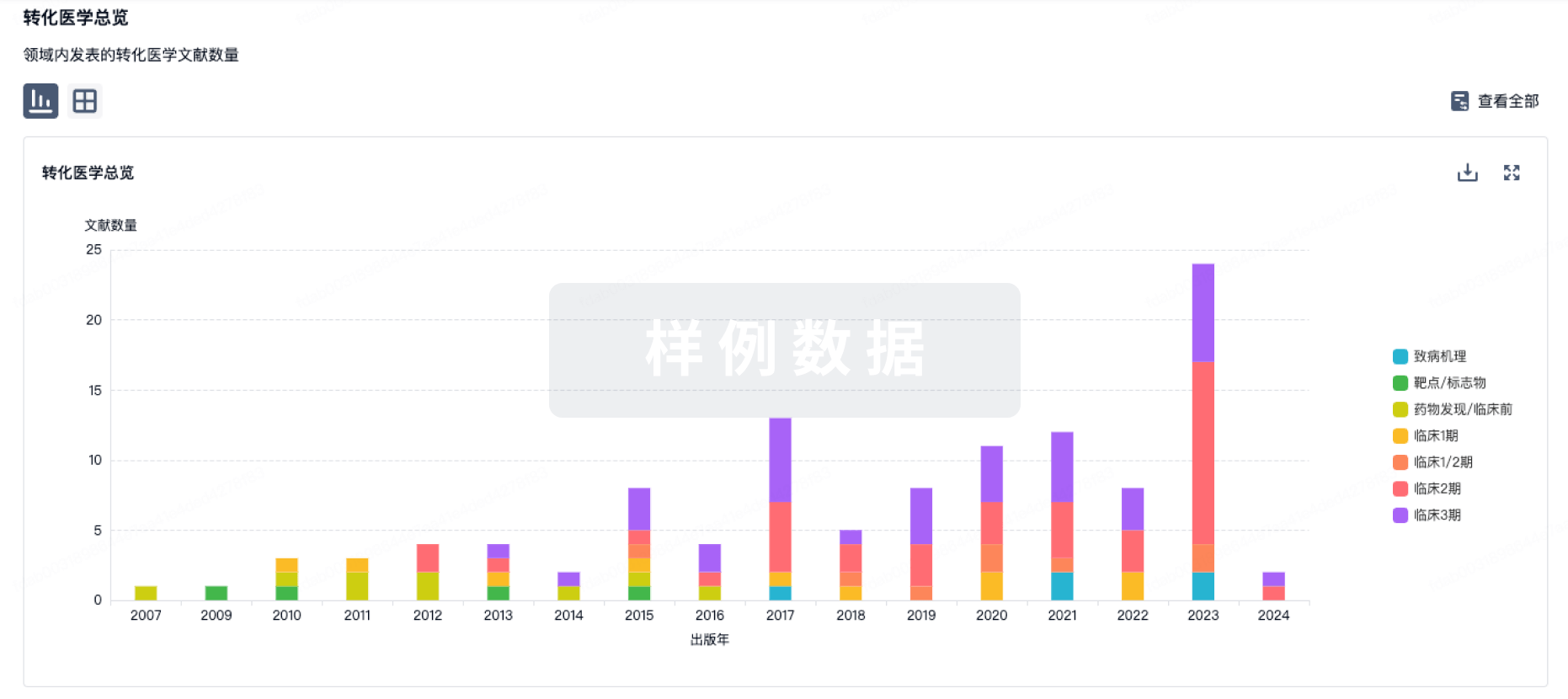
100 项与 Nicotinamide riboside/Pterostilbene 相关的转化医学
登录后查看更多信息
100 项与 Nicotinamide riboside/Pterostilbene 相关的专利(医药)
登录后查看更多信息
1
项与 Nicotinamide riboside/Pterostilbene 相关的文献(医药)2022-10-10·Human molecular genetics
Gene expression profiles in sporadic ALS fibroblasts define disease subtypes and the metabolic effects of the investigational drug EH301
Article
作者: Casalena, Gabriella ; Fels, Jasmine A ; Konrad, Csaba ; Holmes, Holly E ; Manfredi, Giovanni ; Dellinger, Ryan W
Abstract:
Metabolic alterations shared between the nervous system and skin fibroblasts have emerged in amyotrophic lateral sclerosis (ALS). Recently, we found that a subgroup of sporadic ALS (sALS) fibroblasts (sALS1) is characterized by metabolic profiles distinct from other sALS cases (sALS2) and controls, suggesting that metabolic therapies could be effective in sALS. The metabolic modulators nicotinamide riboside and pterostilbene (EH301) are under clinical development for the treatment of ALS. Here, we studied the transcriptome and metabolome of sALS cells to understand the molecular bases of sALS metabotypes and the impact of EH301. Metabolomics and transcriptomics were investigated at baseline and after EH301 treatment. Moreover, weighted gene coexpression network analysis (WGCNA) was used to investigate the association of the metabolic and clinical features. We found that the sALS1 transcriptome is distinct from sALS2 and that EH301 modifies gene expression differently in sALS1, sALS2 and the controls. Furthermore, EH301 had strong protective effects against metabolic stress, an effect linked to the antiinflammatory and antioxidant pathways. WGCNA revealed that the ALS functional rating scale and metabotypes are associated with gene modules enriched for the cell cycle, immunity, autophagy and metabolic genes, which are modified by EH301. The meta-analysis of publicly available transcriptomic data from induced motor neurons by Answer ALS confirmed the functional associations of genes correlated with disease traits. A subset of genes differentially expressed in sALS fibroblasts was used in a machine learning model to predict disease progression. In conclusion, multiomic analyses highlighted the differential metabolic and transcriptomic profiles in patient-derived fibroblast sALS, which translate into differential responses to the investigational drug EH301.
739
项与 Nicotinamide riboside/Pterostilbene 相关的新闻(医药)2026-02-26
在主要终点上, orforglipron 36mg组糖化血红蛋白(A1C)降幅为2.2%,而口服司美格鲁肽14mg组为1.4%。
在一项关键次要终点方面,orforglipron 36mg组参与者体重平均下降8.9kg(9.2%),而口服司美格鲁肽14mg组为5.0kg(5.3%),前者实现了73.6%更高的相对体重减轻幅度。
礼来已向全球40多个国家的监管机构提交orforglipron的上市申请,预计美国将于2026年第二季度就其肥胖适应症作出审批决定。
2026年2月26日,礼来公布了ACHIEVE-3研究的详细结果,ACHIEVE-3是该研究系列的首个头对头对照研究,旨在评估orforglipron与口服司美格鲁肽在经二甲双胍治疗血糖控制不佳的2型糖尿病成人患者中的安全性和有效性。orforglipron是一种小分子口服GLP-1受体激动剂,服用时没有饮食或饮水限制。该研究为期52周,共纳入1,698名参与者,分为四个活性治疗组:orforglipron 12mg和36mg,以及口服司美格鲁肽7mg和14mg。在ACHIEVE-3研究中,orforglipron在主要终点及所有关键次要终点上均优于口服司美格鲁肽,在降低A1C和体重改善方面取得显著提升。1,2相关研究结果今日发表于《柳叶刀》。
主要研究者、德克萨斯大学西南医学中心临床医学教授Julio Rosenstock博士表示:
ACHIEVE-3为我们首次提供了两种口服GLP-1受体激动剂在2型糖尿病成人患者中的头对头比较数据,且所观察到的差异具有明确的临床意义,在我们评估的所有关键终点上,包括A1C和体重减轻,orforglipron 12mg和36mg剂量均优于口服司美格鲁肽7mg和14mg剂量。相关改善最早在治疗第4周即可显现,并在整个研究期间持续保持。
上海交通大学医学院附属第六人民医院贾伟平教授作为ACHIEVE-3研究中国主要研究者,表示:
ACHIEVE3研究在中国近20个城市开展,纳入百余名中国患者。研究结果显示,orforglipron在我国人群中展现出与全球一致的有效性和安全性,为未来2型糖尿病治疗格局带来了新的可能,也为我国临床实践提供了重要参考。
当前,很多2型糖尿病患者在治疗过程中仍面临依从性挑战。Orforglipron通过突破口服肽类GLP-1受体激动剂在给药时间、进食和饮水方面的严格限制,使治疗更贴合患者的日常生活节奏。其兼具疗效与便利性的特性,有望为更多患者提供一种既易坚持、又能真正改善长期管理体验的治疗方案。
ACHIEVE-3 研究结果
ip<0.001 vs. 口服司美格鲁肽7mg
iip<0.001 vs. 口服司美格鲁肽14mg
iiip<0.01 vs. 口服司美格鲁肽14mg
iv未对orforglipron 12mg与口服司美格鲁肽14mg剂量组的体重对比以及实现A1C <5.7%的参与者比例进行整体I类错误率控制。 1
此外,orforglipron在多项关键心血管风险因素方面亦显示出具有临床意义的改善,包括非HDL胆固醇、HDL胆固醇、VLDL胆固醇、总胆固醇、收缩压及甘油三酯。4
礼来执行副总裁、心血管代谢健康事业部总裁Kenneth Custer博士表示:
ACHIEVE-3研究结果凸显了orforglipron在2型糖尿病治疗中相较口服司美格鲁肽的潜在优势:更大幅度的A1C降低、更显著的体重减轻,以及无需限制饮食或饮水的给药便捷性——这一组合优势对于需要日常管理疾病的患者而言意义重大。随着全球申报工作的推进,以及FDA预计于下季度对肥胖适应症作出决定,礼来正致力于尽快将这一治疗选择带给患者。
在ACHIEVE-3研究中,orforglipron的整体安全性和耐受性特征与此前研究结果一致。对于orforglipron及口服司美格鲁肽,最常见的不良事件包括恶心、腹泻、呕吐、消化不良和食欲下降。orforglipron因不良事件导致的治疗中断率为12mg组8.7%和36mg组9.7%,而口服司美格鲁肽为7mg组4.5%和14mg组4.9%。
礼来已向全球包括中国在内的40多个国家监管机构提交orforglipron上市申请,并计划于今年晚些时候在美国提交用于治疗2型糖尿病的申请。
关于orforglipron
Orforglipron是一种在研的、每日一次口服的小分子(非肽类)胰高血糖素样肽 – 1受体激动剂(GLP-1 RA)。该药物可在全天任何时间服用,对饮食和饮水不加以限制。5该药物由中外制药(Chugai Pharmaceutical Co., Ltd.)发现,并于2018年授权至礼来公司开发。中外制药与礼来共同发表了这一分子的临床前药理学数据。6目前,礼来正在进行orforglipron用于治疗2型糖尿病,以及用于肥胖或至少伴有一种体重相关合并症的超重成人进行体重管理的系列3期研究。此外,礼来还在研究orforglipron作为治疗肥胖成人的阻塞性睡眠呼吸暂停和高血压的潜在可能。
关于ACHIEVE-3和
ACHIEVE临床研究项目
ACHIEVE-3(NCT06045221)是一项为期52周的3期随机、开放标签临床研究,旨在评估在经二甲双胍血糖控制不佳的2型糖尿病成人参与者中,orforglipron与口服司美格鲁肽的疗效和安全性。该研究共纳入来自美国、阿根廷、中国、日本、墨西哥和波多黎各的1,698名参与者,以1:1:1:1的比例随机分配接受orforglipron (12mg或36mg),或口服司美格鲁肽 (7mg 或14mg)。研究的主要目标是证明orforglipron低剂量及高剂量组在52周时的A1C降幅非劣于口服司美格鲁肽。所有接受orforglipron治疗的参与者均以1mg每日一次的剂量起始,每4周增加一次剂量,直至达到最终随机维持剂量:12mg(从1mg起始、增至3mg、再至6mg)或36mg(从1mg起始、增至3mg、再至6mg、12mg和24mg)。所有接受口服司美格鲁肽治疗的参与者均以3mg每日一次的剂量起始,每4周增加一次剂量,直至达到最终随机维持剂量7mg(从3mg起始)或14mg(从3mg起始、增至7mg)。如果参与者无法耐受orforglipron或司美格鲁肽的某一剂量,可在研究期间回退一次至前一剂量,orforglipron的最低剂量为3mg,口服司美格鲁肽的最低剂量为7mg。
Orforglipron的ACHIEVE 3期全球临床开发项目已招募了超过6,000名2型糖尿病参与者入组5项全球注册研究。该项目于2023年启动,预计将于今年或2026年公布结果。
参考文献
Please scroll down for more.
All measures except for body weight for orforglipron 12 mg vs. oral semaglutide 14 mg and percentage of participants achieving A1C <5.7% were controlled for family-wise type 1 error using the efficacy estimand and treatment-regimen estimand. Body weight for orforglipron 12 mg vs. oral semaglutide 14 mg and percentage of participants achieving A1C <5.7% were prespecified secondary endpoints and showed nominal statistical significance using the efficacy estimand.
The efficacy estimand represents efficacy had all randomized participants remained on study intervention (with possible dose interruptions and/or dose modifications) for 52 weeks without initiating additional antihyperglycemic medications (>14 days of use).
The treatment-regimen estimand represents the estimated average treatment effect regardless of adherence to study intervention or initiation of additional antihyperglycemic medications.
Not controlled for family-wise type 1 error.
Ma X, Liu R, Pratt EJ, Benson CT, Bhattachar SN, Sloop KW. Effect of Food Consumption on the Pharmacokinetics, Safety, and Tolerability of Once-Daily Orally Administered Orforglipron (LY3502970), a Non-peptide GLP-1 Receptor Agonist. Diabetes Ther. 2024 Apr;15(4):819-832. https://doi.org/10.1007/s13300-024-01554-1. Epub 2024 Feb 24. PMID: 38402332; PMCID: PMC10951152.
Kawai T, Sun B, Yoshino H, Feng D, Suzuki Y, Fukazawa M, Nagao S, Wainscott DB, Showalter AD, Droz BA, Kobilka TS, Coghlan MP, Willard FS, Kawabe Y, Kobilka BK, & Sloop KW, Structural basis for GLP-1 receptor activation by LY3502970, an orally active nonpeptide agonist, Proc. Natl. Acad. Sci. U.S.A. 117 (47) 29959-29967, https://doi.org/10.1073/pnas.2014879117 (2020).
Lilly
关于礼来公司
礼来公司是一家致力于通过科学创新改善人类健康水平,惠及全球患者的医药公司。作为医疗健康行业的领军者,礼来公司拥有近150年的历史。今天,我们的药物已帮助全球数千万人。运用生物技术、化学和基因医学的力量,我们的科学家正在积极推动新的医学进展,以应对严峻的全球健康挑战。重新定义糖尿病与肥胖疗法,减少肥胖对人体的长期影响;助力阿尔茨海默病的防治行动;为一系列威胁人类健康的免疫性疾病提供解决方案;以及将难以治愈的癌症转变为可控的疾病。礼来公司迈向健康世界的每一步,都源自于我们“致力于让数百万患者生活得更美好”的信念。这包括致力于解决全球多重挑战的创新临床试验,同时确保药物的可及性和可负担性。如果需要了解更多关于礼来公司的信息,请登录:www.lilly.com.cn。
CMAT-15606
2026-02-26
点击蓝字,关注我们
1979年,纽约纪念医院斯隆凯特林癌症中心首次在化学或病毒诱发的肿瘤细胞中,发现一种分子量为53千道尔顿的蛋白质,并将其命名为p53,但是正常细胞并未发现p53,此后10年一直不知p53对肿瘤的确切作用。1989年,霍普金斯大学发现人类肿瘤常见p53编码基因TP53发生突变,利用基因编辑技术删除小鼠p53编码基因Trp53以后也会快速发生肿瘤。这些发现确定p53对肿瘤具有抑制功能,随后几十年研究证实人类肿瘤TP53基因突变率最高,人类乳腺癌TP53基因突变率可达30%至50%,尤其三阴性乳腺癌高达70%至80%。p53属于基因转录因子,通过多种途径调控数百个靶基因表达,防止基因组突变,从而维持细胞和组织基因组稳定并抑制肿瘤生长,故又被称为基因组守护神。这些途径包括抑制细胞生长、诱导细胞在应激反应中死亡以及维持基因组完整和代谢稳定(图A)。p53一端是转录激活区,中间是DNA结合区,以特定序列控制靶基因表达,另一端是四聚体区,可非特异结合DNA。大多数突变影响中间DNA结合区,包含锌指结构,对p53结构稳定至关重要(图B)。这些突变大多为原有氨基酸被其他氨基酸取代的错义突变,从而破坏p53结构或阻止其与DNA结合。由于某些氨基酸比其他氨基酸更容易发生突变,因此被称为热点突变(图B)。
2013年,根据法国和瑞典学者估计,全球大约2000万例被诊断癌症患者其中一半携带突变型TP53基因,且突变发生于一或两个等位基因。不过,另一半患者携带野生型TP53基因,p53抑癌功能通常受损。野生型p53半衰期短,表达水平低。突变型p53通常半衰期延长,并在癌细胞中积累。因此,恢复p53抑癌功能(无论TP53是否突变)对癌症治疗具有巨大的潜力,科学家开展大量研究尝试恢复野生型或突变型p53功能。
恢复野生型p53功能
p53关键转录靶点之一为泛素连接酶编码基因MDM2,该酶能够结合并标记p53氨基端,从而让p53被蛋白酶体降解。因此,p53对MDM2的转录激活是p53自身调控环路的一部分,目前大量精力被投入开发能够阻止MDM2结合从而增强野生型p53功能的小分子药物。
恢复突变型p53功能
无义突变常见于抑癌基因,通常导致基因编码蛋白质功能丧失。不过,TP53突变仅8%为无义突变,超过73%为错义突变,可能导致原有氨基酸残基被其他氨基酸残基取代。例如,TP53突变之一Y220C特征为第220位氨基酸残基的酪氨酸(Y)被半胱氨酸(C)取代。TP53错义突变发生率较高,促使科学家寻找能够恢复突变型p53抑癌功能的小分子药物。
实际上,近25年来已有11种小分子药物被报告能够重新激活突变型p53功能。其中,PRIMA首先被报告通过与DNA结合区半胱氨酸残基结合,可恢复突变型p53的结构、转录活性和细胞生长抑制功能。随后,PRIMA甲基化衍生物APR-246被研发,并进入一期和二期临床试验,但是三期临床试验失败。
近年来,科学家结合计算机建模和化学库筛选,发现三氧化二砷(俗称砒霜)是有效的突变型p53激活剂。突变型p53(R175H)与三氧化二砷复合物的晶体结构显示,三氧化二砷与p53锌指结构区的半胱氨酸残基结合。该结合使许多结构缺陷的突变型p53重新折叠为野生型结构,从而恢复转录活性。三氧化二砷为一线临床药物,通常与全反式维甲酸联合用于治疗急性早幼粒细胞白血病,并已注册三氧化二砷治疗多种癌症的一期、二期和三期临床试验。
在由TP53热点突变产生的p53突变蛋白中,Y220C突变残基形成的口袋结构容易与小分子药物结合,并有可能改变其结构,因此对靶向药物研究具有吸引力。该突变存在于大约1%的p53突变型癌症,大约10万癌症患者携带该突变。2008年,英国剑桥大学结合体外热变性和计算机建模筛选方法,发现一种小分子能够将Y220C突变型p53恢复为野生型p53结构。随后12年,根据英国剑桥大学的研究结果,至少10种Y220C突变型p53激活药物被研发,但是结合亲和力都较低。最后,美国PMV制药研发的瑞泽泊特,与突变型p53的结合亲和力最高,小鼠研究表明瑞泽泊特能够有选择地恢复TP53转录活性,并抑制肿瘤生长。
2026年2月25日,国际四大医学期刊之一、创刊于1812年的美国麻省医学会官方期刊《新英格兰医学杂志》在线发表德克萨斯大学MD安德森癌症中心、哈佛大学医学院德纳法伯癌症中心、麻省总医院、莎拉坎农研究中心、奥斯汀NEXT癌症中心、弗雷德哈钦森癌症中心、南加利福尼亚大学诺里斯综合癌症中心、俄勒冈医科大学奈特癌症中心、克利夫兰医学中心、PMV制药、纽约纪念医院斯隆凯特林癌症中心的PYNNACLE研究报告,首次探讨了瑞泽泊特对TP53基因Y220C突变实体肿瘤人类患者的剂量、有效性和安全性。
NCT04585750: The Evaluation of PC14586 in Patients With Advanced Solid Tumors Harboring a TP53 Y220C Mutation (PYNNACLE)
Official Title: A Phase 1/2 Open-label, Multicenter Study to Assess the Safety, Tolerability, Pharmacokinetics, Pharmacodynamics, and Efficacy of PC14586 in Patients With Locally Advanced or Metastatic Solid Tumors Harboring a TP53 Y220C Mutation (PYNNACLE)
该多中心单组非盲剂量递增和剂量优化一期临床研究入组携带TP53基因Y220C突变实体肿瘤局部晚期或远处转移经过一至九线(中位三线)治疗失败患者77例(其中乳腺癌10例)口服瑞泽泊特治疗连续21天,每天1次150至2500毫克或每天2次1500毫克。主要目标为确定最大耐受剂量和二期临床研究推荐剂量。主要终点包括剂量限制性毒性和不良事件,次要终点包括初步疗效和药物代谢动力学特征。
结果,截至2023年12月15日,最大耐受剂量为每天2次1500毫克。根据安全性、有效性和药物代谢动力学数据,选择每天1次2000毫克与食物同服作为二期研究推荐剂量。
治疗期间,76例患者(99%)至少出现过1次不良事件,其中29例(38%)出现过1级或2级不良事件。最常见的不良事件为恶心(58%)、呕吐(44%)、血肌酐升高(39%)、疲乏(39%)和贫血(36%)。67例患者(87%)出现治疗相关不良事件,其中48例(62%)为1级或2级不良事件;2例患者(3%)由于治疗相关不良事件而停用瑞泽泊特。大多数胃肠不良事件经症状治疗后缓解,且与食物同服时不良事件发生率较低。贫血是治疗期间最常见的≥3级不良事件,发生率为16%。
全部患者总缓解率(完全缓解或部分缓解)为20%,KRAS基因野生型肿瘤且每天1次至少1150毫克剂量治疗患者总缓解率为30%。对于多种肿瘤都观察到确认缓解,包括卵巢癌和乳腺癌。全部缓解患者均为携带TP53基因Y220C突变和KRAS野生型的实体肿瘤。
因此,该一期临床研究结果表明,对于TP53基因Y220C突变实体肿瘤经过大量治疗失败患者,瑞泽泊特最常见不良反应为恶心和呕吐,乳腺癌等多种肿瘤都观察到抗肿瘤活性,可为p53再次激活提供概念验证。
对此,英国牛津大学路德维希癌症研究院发表同期社论:实体肿瘤突变型p53功能恢复。
N Engl J Med. 2026 Feb 25;394(9):872-883. IF: 78.5
Phase 1 Study of Rezatapopt, a p53 Reactivator, in TP53 Y220C-Mutated Tumors.
Dumbrava EE, Shapiro GI, Parikh AR, Johnson ML, Tolcher AW, Thompson JA, El-Khoueiry AB, Vandross AL, Kummar S, Shepard DR, LeDuke K, Sheehan L, Alland L, Haque A, Jalota D, Fellous M, Schram AM.
University of Texas M.D. Anderson Cancer Center, Houston; Dana-Farber Cancer Institute, Boston; Massachusetts General Hospital, Boston; Sarah Cannon Research Institute, Nashville; NEXT Oncology, Austin, Texas; Fred Hutchinson Cancer Center, Seattle; University of Southern California Norris Comprehensive Cancer Center, Los Angeles; Oregon Health and Science University Knight Cancer Institute, Portland; Cleveland Clinic Foundation, Cleveland; PMV Pharmaceuticals, Princeton, NJ; Leila Alland MD Consultancy, New York; Memorial Sloan Kettering Cancer Center, New York.
BACKGROUND: Rezatapopt is an investigational, first-in-class, oral, selective p53 reactivator that specifically binds to Y220C-mutated p53, which stabilizes p53 in its wild-type conformation and restores its functionality.
METHODS: In this phase 1, single-group, dose-escalation and dose-optimization study, we assigned heavily pretreated patients with locally advanced or metastatic solid tumors harboring a TP53 Y220C mutation to receive rezatapopt during continuous 21-day treatment cycles. The primary objectives were to determine the maximum tolerated dose and recommended phase 2 dose. Primary end points included dose-limiting toxic effects and adverse events. Secondary end points included preliminary efficacy and pharmacokinetic features.
RESULTS: A total of 77 patients received rezatapopt at one of eight escalating doses: 150 mg, 300 mg, 600 mg, 1150 mg, 1500 mg, 2000 mg, or 2500 mg once daily or 1500 mg twice daily. The maximum tolerated dose was 1500 mg twice daily. On the basis of safety, efficacy, and pharmacokinetic data, 2000 mg once daily with food was selected as the recommended phase 2 dose. During the treatment period, 76 patients (99%) had at least one adverse event and 29 (38%) had an adverse event of grade 1 or 2. The most common adverse events were nausea (in 58% of patients), vomiting (in 44%), an increased blood creatinine level (in 39%), fatigue (in 39%), and anemia (in 36%). Treatment-related adverse events occurred in 67 patients (87%) and those of grade 1 or 2 in 48 (62%); 2 patients (3%) discontinued rezatapopt because of a treatment-related adverse event. Most gastrointestinal adverse events resolved with the treatment of symptoms and were less frequent when rezatapopt was given with food. Anemia was the most common adverse event of grade 3 or higher during the treatment period, occurring in 16% of patients. The overall response (complete or partial response) was 20% among all patients and 30% among those who had a KRAS wild-type tumor and received a dose of at least 1150 mg once daily. Confirmed responses were seen across multiple tumor types, including ovarian and breast cancers. All patients with a response had a solid tumor that harbored TP53 Y220C and wild-type KRAS.
CONCLUSIONS: In this phase 1 study involving heavily pretreated patients, the most common adverse events associated with rezatapopt were nausea and vomiting. Antitumor activity occurred across multiple tumor types, providing proof of concept for p53 reactivation.
Funded by PMV Pharmaceuticals
PYNNACLE ClinicalTrials.gov number, NCT04585750
PMID: 41740031
DOI: 10.1056/NEJMoa2508820
N Engl J Med. 2026 Feb 25;394(9):922-925. IF: 78.5
Restoring Function to a Variant of p53 in Solid Tumors.
Lu X.
Ludwig Institute for Cancer Research, University of Oxford, Oxford, United Kingdom.
PMID: 41740037
DOI: 10.1056/NEJMe2516747
(来源:SIBCS)
声 明
凡署名原创的文章版权属《肿瘤瞭望》所有,欢迎分享、转载。本文仅供医疗卫生专业人士了解最新医药资讯参考使用,不代表本平台观点。该等信息不能以任何方式取代专业的医疗指导,也不应被视为诊疗建议,如果该信息被用于资讯以外的目的,本站及作者不承担相关责任。
2026-02-25
注册号:
Registration number:
ChiCTR2600119266 最近更新日期:
Date of Last Refreshed on:
2026-02-25 09:33:22 注册时间:
Date of Registration:
2026-02-25 00:00:00 注册号状态:
预注册Registration Status:
Prospective registration注册题目:
评价CMS-D001在中度至重度特应性皮炎患者中的有效性和安全性的多中心、 随机、双盲、安慰剂对照的Ⅱ期临床研究Public title:
A multicenter, randomized, double-blind, placebo-controlled Phase II clinical study evaluating the efficacy and safety of CMS-D001 in patients with moderate to severe atopic dermatitis注册题目简写:English Acronym:研究课题的正式科学名称:
评价CMS-D001在中度至重度特应性皮炎患者中的有效性和安全性的多中心、 随机、双盲、安慰剂对照的Ⅱ期临床研究Scientific title:
A multicenter, randomized, double-blind, placebo-controlled Phase II clinical study evaluating the efficacy and safety of CMS-D001 in patients with moderate to severe atopic dermatitis研究课题代号(代码):
Study subject ID:在二级注册机构或其它机构的注册号:
The registration number of the Partner Registry or other
register:申请注册联系人:
陈权
研究负责人:
崔勇 Applicant:
Chen Quan
Study leader:
Cui yong 申请注册联系人电话:
Applicant telephone:
+86 177 0885 7150
研究负责人电话:
Study leader's telephone:
+86 157 0162 5913申请注册联系人传真 :
Applicant Fax:
研究负责人传真:
Study leader's fax:申请注册联系人电子邮件:
Applicant E-mail:
chenquan@cms.net.cn
研究负责人电子邮件:
Study leader's E-mail:
wuhucuiyong@vip.163.com申请单位网址(自愿提供):
Applicant website(voluntary supply):
研究负责人网址(自愿提供):
Study leader's website(voluntary supply):申请注册联系人通讯地址:
中国广东省深圳市南山区南头街道马家龙社区南山大道3186号莲花广场B栋801
研究负责人通讯地址:
中国北京市朝阳区文学馆路47号Applicant address:
Room 801, Building B, Lianhua Plaza, 3186 Nanshan Avenue, Majalong Community, Nantou Street, Nanshan District, Shenzhen, Guangdong, China
Study leader's address:
No. 47, Wenxueguan Road, Chaoyang District, Beijing, China申请注册联系人邮政编码:
Applicant postcode:
研究负责人邮政编码:
Study leader's postcode:申请人所在单位:
海南德镁医药科技有限责任公司Applicant's institution:
Hainan Dermavon Pharmaceutical Technology Co., Ltd.研究负责人所在单位:
中日友好医院Affiliation of the Leader:
China-Japan Friendship Hospital是否获伦理委员会批准:
是Approved by ethic committee:
Yes伦理委员会批件文号:
Approved No. of ethic committee:
YW2025-097-01
伦理委员会批件附件:
Approved file of Ethical Committee:
查看附件View批准本研究的伦理委员会名称:
中日友好医院药物(器械)临床试验伦理委员会Name of the ethic committee:
Ethics Committee for Drug (Device) Clinical Trials at Sino-Japanese Friendship Hospital伦理委员会批准日期:
Date of approved by ethic committee:
2025-12-29 00:00:00伦理委员会联系人:
郤思远Contact Name of the ethic committee:
Xi Siyuan伦理委员会联系地址:
中国北京市朝阳区樱花东街2号制剂楼415Contact Address of the ethic committee:
No. 415, Preparation Building, Yinghua Dong Street, Chaoyang District, Beijing, China伦理委员会联系人电话:
Contact phone of the ethic committee:
+86 10 8420 6086
伦理委员会联系人邮箱:
Contact email of the ethic committee:研究实施负责(组长)单位:
中日友好医院Primary sponsor:
China-Japan Friendship Hospital研究实施负责(组长)单位地址:
中国北京市朝阳区文学馆47号Primary sponsor's address:
No. 47, Wenxueguan Road, Chaoyang District, Beijing, China试验主办单位(项目批准或申办者):
Secondary sponsor:
国家:
中国
省(直辖市):
海南
市(区县):
Country:
China
Province:
Hainan
City:
单位(医院):
海南德镁医药科技有限责任公司
具体地址:
中国海南省海口市国家高新技术产业开发区科技大道22号海口国科中心C座6楼整层
Institution
hospital:
Hainan Dermavon Pharmaceutical Technology Co., Ltd.
Address:
6th Floor, Block C, Haikou National Science and Technology Center, No. 22 Science and Technology Avenue, National High tech Industrial Development Zone, Haikou, Hainan, China经费或物资来源:
海南德镁医药科技有限责任公司Source(s) of funding:
Hainan Dermavon Pharmaceutical Technology Co., Ltd.研究疾病:
特应性皮炎 Target disease:
Atopic dermatitis研究疾病代码:Target disease code:研究类型:
干预性研究Study type:
Interventional study研究所处阶段:
II期临床试验 Study phase:
2研究设计:
随机平行对照 Study design:
Parallel 研究目的:
主要目的:
评价CMS-D001在中度至重度特应性皮炎参与者中的初步有效性。
次要目的:
评价CMS-D001在中度至重度特应性皮炎参与者中的安全性和耐受性。
评价CMS-D001及其主要代谢产物(如适用)在中度至重度特应性皮炎参与者中的药代动力学(PK)特征。
评价CMS-D001及其主要代谢产物(如适用)在中度至重度特应性皮炎参与者中的暴露-效应(E-R)关系。 Objectives of Study:
Primary Objective:
To evaluate the preliminary efficacy of CMS-D001 in participants with moderate to severe atopic dermatitis.
Secondary objective:
Evaluate the safety and tolerability of CMS-D001 in participants with moderate to severe atopic dermatitis.
Evaluate the pharmacokinetic (PK) profile of CMS-D001 and its major metabolites (if applicable) in participants with moderate to severe atopic dermatitis.
Evaluate the exposure-response (E-R) relationship of CMS-D001 and its major metabolites (if applicable) in participants with moderate to severe atopic dermatitis.药物成份或治疗方案详述:
Description for medicine or protocol of treatment in
detail:
纳入标准:
入选标准:
参与者必须符合下列所有标准才能参加试验:
(1) 自愿签署知情同意书(ICF),能够和研究者进行良好的沟通,并且理解和遵守本研究的各项要求和限制条件;
(2) 签署ICF时,年龄≥18周岁且≤75周岁,性别不限;
(3) 筛选/基线访视时按照Hanifin & Rajka标准(1980)经研究者确诊为AD(附录1),且自首次出现AD相关皮疹/症状至筛选时病程≥1年;
(4) 筛选和基线时,根据研究者评估,符合中重度AD标准:
湿疹面积和严重程度指数(EASI)评分≥16;
研究者总体评估(IGA)评分≥3;
受累体表面积(BSA)≥10%;
瘙痒数字评分量表(Itch NRS)评分≥4;
(5) 经研究者判断,参与者具有对外用皮质类固醇(TCS)或外用钙调神经磷酸酶抑制剂(TCI)治疗反应不佳或不耐受的病史,或其他医学上考虑不建议进行外用治疗;
(6) 能够且愿意从基线前至少7天开始,仅使用由申办者统一提供的不含影响疗效评价成分的润肤剂,并在研究期间持续使用;
(7) 所有具有生育潜能的女性参与者及所有男性参与者需自签署ICF至研究末次给药后至少3个月无怀孕或捐精计划,必须遵守避孕的相关规定,至少采用一种高效的避孕方法避孕。(注:与有生育潜能的女性伴侣同居的男性参与者,必须愿意在其伴侣使用高效避孕方法的基础上再使用安全套)。Inclusion criteria
Inclusion criteria:
Participants must meet all of the following criteria to participate in the trial:
(1) Voluntarily sign an informed consent form (ICF), be able to communicate well with the researcher, and understand and comply with the requirements and limitations of this study;
(2) When signing the ICF, the age should be between 18 and 75 years old, with no gender restrictions;
(3) During screening/baseline visits, the patient was diagnosed with AD by the researcher according to Hanifin&Rajka criteria (1980) (Appendix 1), and the disease duration from the first appearance of AD related rash/symptoms to screening was >= 1 year;
(4) During screening and baseline, according to the researcher's evaluation, it meets the criteria for moderate to severe Alzheimer's disease:
Eczema area and severity index (EASI) score >= 16;
Researcher's overall assessment (IGA) score >= 3;
Affected body surface area (BSA) >= 10%;
Itch NRS score >= 4;
(5) According to the researchers' judgment, the participants have a history of poor response or intolerance to external corticosteroids (TCS) or external calcineurin inhibitors (TCI) treatment, or other medical considerations do not recommend external treatment;
(6) Able and willing to use only moisturizers provided by the sponsor that do not contain ingredients that affect efficacy evaluation, starting at least 7 days before baseline, and continue to use them during the study period;
(7) All female participants with reproductive potential and all male participants must sign the ICF and have no pregnancy or sperm donation plan for at least 3 months after the last dose of the study. They must comply with contraception regulations and use at least one highly effective contraceptive method . (Note: Male participants who cohabit with female partners with reproductive potential must be willing to use condoms on the basis of their partner's use of efficient contraceptive methods).排除标准:
排除标准:
必须排除符合下列任一排除标准的参与者:
(1) 患有其他混淆AD诊断或影响疗效评估的其他皮肤病(如全身性红皮病、银屑病、红斑狼疮、Netherton综合征等)、皮肤感染,或在患处有色素沉着、瘢痕、胎斑、纹身等情况经研究者判断可能影响对皮肤病变的评价;
(2) 有严重带状疱疹或严重单纯疱疹既往史(包括但不限于播散型带状疱疹、泛发型带状疱疹、中枢神经系统带状疱疹、眼带状疱疹、复发性带状疱疹(2年内发生2次或以上)或有单纯疱疹、带状疱疹感染现病史;
(3) 首次给药前3个月内存在需住院或静脉抗感染治疗的细菌、真菌或病毒感染史;
(4) 首次给药前4周内存在需口服抗感染治疗的细菌、真菌或病毒感染史;
(5) 首次给药前7天内,存在活动性感染或急性疾病状态(如发热、恶心、呕吐或腹泻);
(6) 筛选或基线时,存在慢性或复发性感染性疾病者,包括但不限于慢性肾脏感染、复发性尿路感染、慢性胸部感染、真菌感染(指甲浅表真菌感染除外)或感染性的皮肤伤口或溃疡,经研究者评估可能增加参与者安全性风险;
(7) 符合以下任一项结核筛查标准:
有活动性结核感染的现病史或既往病史;
在筛选期间,研究者判断存在活动性结核病的体征或症状;
胸部CT提示当前或既往活动性结核感染;
γ-干扰素释放试验结果显示潜伏性结核感染证据,定义为:筛选时γ-干扰素释放试验检测呈阳性或连续两次γ-干扰素释放试验结果不确定,且无临床症状。除非有记录表明参与者已经完成充分的结核潜伏感染的治疗,或者在首次给药前至少4周开始预防性治疗,并且同意完成后续预防性治疗疗程,预防措施的整个疗程不必在首次给药前完成。
注:
1)不允许使用利福平或利福喷丁进行结核预防。
2)如结核检测结果为不确定者,可进行1次复测。
(8) 首次给药前4周内接种减毒活疫苗,或计划在治疗期间的任何时间或研究完成后8周内接种减毒活疫苗者;
(9) 首次给药前6个月内存在重大或不稳定的消化/肝胆、肾脏/泌尿、心血管、呼吸、内分泌、血液、免疫、中枢神经系统疾病者,根据研究者判断不具备临床研究条件者,例如但不限于胰腺炎、不稳定型心绞痛、心肌梗死、症状性充血性心力衰竭(纽约心脏病协会III级或IV级)、需要治疗的心律失常、药物控制不佳的高血压(收缩压≥160mmHg,舒张压≥100mmHg)、肺动脉高压、呼吸衰竭、脑卒中(包含短暂性脑缺血发作)、肝硬化、静脉血栓栓塞症等;
(10) 首次给药前5年内患有恶性肿瘤(经过彻底治疗且没有任何复发迹象的皮肤原位鳞癌、基底细胞癌和原位宫颈癌除外)或淋巴组织增生性疾病;
(11) 目前患有其它自身免疫性疾病(如类风湿性关节炎、系统性红斑狼疮、炎症性肠病等);
(12) 患有或疑似先天性或获得性免疫缺陷病史者,或研究者认为会损害参与者免疫状态的情况(如脾切除术史、原发性免疫缺陷);
(13) 患有精神相关疾病或病史(如抑郁症),影响用药依从性或研究者从临床上判断有自杀风险者;
(14) 既往接受过或计划接受器官移植手术且需服用免疫抑制剂的参与者(如肝肾移植);
15.筛选时任何显著的临床和实验室异常,研究者认为可能影响参与者安全者,包括但不限于:
血常规:白细胞<3.0×10^9/L,中性粒细胞<1.5×10^9/L,淋巴细胞计数<0.5×10^9/L;血小板计数<100.0×10^9/L,血红蛋白<100g/L;
肾功能:估算的肾小球滤过率(eGFR)<60mL/min/1.73m^2;
肝功能:丙氨酸转氨酶(ALT)或天冬氨酸转氨酶(AST)≥2×ULN(正常值上限);总胆红素≥1.5×ULN;
任何其它实验室检查结果异常且有临床意义,经研究者评估如果参与研究将可能对参与者构成不可接受的风险;
(16) 筛选或基线时,生命体征、体格检查、12-导联心电图、胸部CT(可接受1个月内的CT检查结果)异常且有临床意义,经研究者评估如果参与研究将可能对参与者构成不可接受的风险;
(17) 筛选访视时存在下列任一感染者:
乙型肝炎:表面抗原(HBsAg)阳性;或核心抗体(HBcAb)阳性,且乙型肝炎病毒脱氧核糖核酸(HBV-DNA)拷贝数阳性(定义为超过研究中心检测值正常范围上限);
丙型肝炎(HCV)抗体阳性,且HCV-RNA拷贝数阳性(定义为超过研究中心检测值正常范围上限);
人类免疫缺陷病毒抗体(HIV Ab)阳性;
梅毒特异性抗体试验阳性(梅毒非特异性抗体RPR或TRUST结果为阴性,并经研究者判断为过去曾感染梅毒但已治愈的参与者除外);
(18) 随机前规定的洗脱期内接受了以下任何一种治疗者:
3个月内(或5个半衰期,以时间较长者为准)接受过生物疗法,包括但不限于度普利尤单抗、司普奇拜单抗等;
4周内(或5个半衰期,以时间较长者为准)接受过已知或可能影响特应性皮炎的系统治疗,包括但不限于JAK1/2/3抑制剂、系统性皮质类固醇或促肾上腺皮质激素类似物、环孢菌素、甲氨蝶呤、硫唑嘌呤或其他系统性免疫抑制或免疫调节剂(如霉酚酸酯或他克莫司);
4周内接受过紫外光治疗或长时间暴露于自然或人工紫外线辐射源(如阳光或日光浴),和/或有意在研究期间接受此类暴露者;
4周内接受过长效抗凝药物(如华法林、氯吡格雷等)或需要持续使用抗凝药物治疗者(≤100mg/天的阿司匹林除外);
2周内接受过已知或可能影响特应性皮炎的外用药物治疗,包括外用糖皮质激素(TCS)、钙调磷酸酶抑制剂(TCI)、磷酸二酯酶4(PDE4)抑制剂等;
2周内接受过用于治疗特应性皮炎的口服中草药或中成药(以下中药需洗脱4周:含明确免疫抑制/强免疫调节成分的中药或中成药,包括但不限于:雷公藤及其制剂、复方甘草酸苷等;组方复杂且成分不清、或无法明确主要有效/活性成分及其停用时间的中药治疗;研究者判断可能对疾病严重程度或免疫状态产生持续影响,干扰疗效评估或增加风险者);
(19) 既往暴露于TYK2抑制剂治疗者,或既往接受过系统性JAK1/2/3抑制剂治疗且疗效不佳或因安全性原因停药的参与者;
(20) 筛选前3个月内有酗酒史和/或药物滥用史;
(21) 存在任何可能影响药物吸收的情况者,包括但不限于:吸收不良综合征、乳糜泻、胃切除术、肠切除术(阑尾切除术除外);
(22) 首次给药前4周或5个半衰期(以时间较长者为准)内使用过或在研究期间不能避免使用CYP3A强诱导剂或抑制剂的药物(见附录7)者;
(23)首次给药前7天内食用了圣·约翰草(贯叶连翘)制品、葡萄柚,或拒绝在整个研究期间(包括随访期)避免食用此类物质者;
(24) 筛选前3个月内献血或失血≥ 400mL或计划在研究期间献血者;
(25) 已知或怀疑对试验药物中任何一种成分过敏者,或任何其他显著的药物过敏(如过敏性休克或肝毒性);
(26) 妊娠或哺乳期女性;
(27) 首次给药前3个月或5个半衰期内(以时间较长者为准)使用其他临床试验药物或目前正在参加其他临床研究者;
(28) 研究者认为不适宜参加本临床研究的其他情况。Exclusion criteria:
Exclusion criteria:
Participants who meet any of the following exclusion criteria must be excluded:
(1) Suffering from other skin diseases (such as systemic erythroderma, psoriasis, lupus erythematosus, Netherton syndrome, etc.) that may confuse the diagnosis of AD or affect the evaluation of treatment efficacy, skin infections, or pigmentation, scars, fetal spots, tattoos, etc. at the affected area, which may affect the evaluation of skin lesions according to the researcher's judgment;
(2) Have a history of severe herpes zoster or severe herpes simplex (including but not limited to disseminated herpes zoster, generalized herpes zoster, central nervous system herpes zoster, ocular herpes zoster, recurrent herpes zoster (occurring twice or more within 2 years), or a current history of herpes simplex or herpes zoster infection;
(3) History of bacterial, fungal, or viral infections requiring hospitalization or intravenous anti infective treatment within 3 months prior to the first administration;
(4) History of bacterial, fungal, or viral infections requiring oral anti infective treatment within 4 weeks prior to the first administration;
(5) Within 7 days before the first administration, there is an active infection or acute disease state (such as fever, nausea, vomiting, or diarrhea);
(6) In screening or baseline, the presence of chronic or recurrent infectious diseases, including but not limited to chronic kidney infection, recurrent urinary tract infection, chronic chest infection, fungal infection (except for superficial nail fungal infection) or infectious skin wounds or ulcers, may increase the safety risk of participants as assessed by the investigator;
(7) Meet any of the following tuberculosis screening criteria:
Present or past medical history of active tuberculosis infection;
During the screening period, the researcher judged that there were signs or symptoms of active tuberculosis;
Chest CT indicates current or previous active tuberculosis infection;
The results of the interferon gamma release test show evidence of latent tuberculosis infection, defined as: positive interferon gamma release test during screening or uncertain results from two consecutive interferon gamma release tests, and no clinical symptoms. Unless there is a record indicating that the participant has completed sufficient treatment for latent tuberculosis infection, or started preventive treatment at least 4 weeks before the first dose, and agrees to complete subsequent preventive treatment courses, the entire course of preventive measures does not need to be completed before the first dose.
Note:
1)The use of rifampicin or rifampicin for tuberculosis prevention is not allowed.
2)If the tuberculosis test result is uncertain, a retest can be conducted once.
(8) Those who have received attenuated live vaccine within 4 weeks before the first administration, or plan to receive attenuated live vaccine at any time during the treatment period or within 8 weeks after the completion of the study;
(9) Patients with significant or unstable digestive/hepatobiliary, renal/urinary, cardiovascular, respiratory, endocrine, hematological, immune, or central nervous system diseases within 6 months prior to the first administration, who, according to the researcher's judgment, do not meet the clinical research conditions, such as but not limited to pancreatitis, unstable angina, myocardial infarction, symptomatic congestive heart failure (New York Heart Association Class III or IV), arrhythmia requiring treatment, poorly controlled hypertension (systolic blood pressure >= 160mmHg, diastolic blood pressure >= 100mmHg), pulmonary hypertension, respiratory failure, stroke (including transient ischemic attack), cirrhosis, venous thromboembolism, etc;
(10) Suffering from malignant tumors (excluding skin squamous cell carcinoma in situ, basal cell carcinoma, and cervical cancer in situ that have been thoroughly treated and show no signs of recurrence) or lymphoproliferative diseases within 5 years before the first administration;
(11) Currently suffering from other autoimmune diseases (such as rheumatoid arthritis, systemic lupus erythematosus, inflammatory bowel disease, etc.);
(12) Individuals with or suspected of having a history of congenital or acquired immunodeficiency, or conditions that researchers believe may impair the immune status of participants (such as a history of splenectomy, primary immunodeficiency);
(13) Individuals with mental illness or medical history (such as depression) that affects medication adherence or is clinically judged by researchers to be at risk of suicide;
(14) Participants who have undergone or plan to undergo organ transplantation surgery and require immunosuppressants (such as liver and kidney transplantation);
(15) Any significant clinical and laboratory abnormalities during screening that researchers believe may affect the safety of participants, including but not limited to:
Blood routine: White blood cell count<3.0 × 10^9/L, neutrophil count<1.5 × 10^9/L, lymphocyte count<0.5 × 10^9/L; platelet count<100.0 × 10^9/L, hemoglobin<100g/L;
Renal function: Estimated glomerular filtration rate (eGFR)<60mL/min/1.73m^2;
Liver function: Alanine transaminase (ALT) or aspartate transaminase (AST) >= 2 × ULN (upper limit of normal); Total bilirubin >= 1.5 × ULN;
Any other laboratory test results that are abnormal and clinically significant, as assessed by the researcher, may pose an unacceptable risk to the participants if they participate in the study;
(16) When screening or baseline, if vital signs, physical examination, 12 lead electrocardiogram, and chest CT (CT scan results within 1 month are acceptable) are abnormal and clinically significant, and the researcher evaluates that participating in the study may pose an unacceptable risk to the participants;
(17) During the screening visit, any of the following infected individuals were identified:
Hepatitis B: HBsAg positive; Or the core antibody (HBcAb) is positive, and the copy number of hepatitis B virus deoxyribonucleic acid (HBV-DNA) is positive (defined as exceeding the upper limit of the normal range of the research center's detection value);
Hepatitis C (HCV) antibody positive and HCV-RNA copy number positive (defined as exceeding the upper limit of the normal range of detection values in the research center);
Positive for Human Immunodeficiency Virus Antibody (HIV Ab);
Positive syphilis specific antibody test (excluding participants who tested negative for syphilis non-specific antibody RPR or TRUST and were diagnosed by the researcher as having previously been infected with syphilis but have been cured);
18. Individuals who received any of the following treatments within the designated elution period prior to randomization:
Received biological therapy within 3 months (or 5 half lives, whichever is longer), including but not limited to Dupilumab, Sprucubizumab, etc;
Within 4 weeks (or 5 half lives, whichever is longer), have received systemic treatments known or likely to affect atopic dermatitis, including but not limited to JAK1/2/3 inhibitors, systemic corticosteroids or adrenocorticotropic hormone analogs, cyclosporine, methotrexate, azathioprine, or other systemic immunosuppressive or immunomodulatory agents (such as mycophenolate mofetil or tacrolimus);
Individuals who have received UV treatment within 4 weeks or have been exposed to natural or artificial UV radiation sources (such as sunlight or sunbathing) for a prolonged period of time, and/or who intend to receive such exposure during the study period;
Those who have received long-acting anticoagulants (such as warfarin, clopidogrel, etc.) within 4 weeks or require continuous use of anticoagulants (excluding aspirin <= 100mg/day);
Within 2 weeks, have received external medication treatment known or likely to affect atopic dermatitis, including topical corticosteroids (TCS), calcineurin inhibitors (TCI), phosphodiesterase 4 (PDE4) inhibitors, etc;
Have received oral Chinese herbal medicine or traditional Chinese patent medicines and simple preparations for the treatment of atopic dermatitis within 2 weeks (the following Chinese medicines need to be eluted for 4 weeks: Chinese herbal medicine or traditional Chinese patent medicines and simple preparations containing clear immunosuppressive/strong immunomodulatory ingredients, including but not limited to: tripterygium wilfordii and its preparations, compound glycyrrhizin, etc.; Chinese herbal medicine treatment with complex formula and unclear ingredients, or the main effective/active ingredients and their stopping time cannot be clear; the researcher judges those who may have a continuous impact on disease severity or immune status, interfere with efficacy evaluation, or increase the risk);
(19) Participants who have been previously exposed to TYK2 inhibitor therapy, or who have previously received systemic JAK1/2/3 inhibitor therapy with poor efficacy or have discontinued medication for safety reasons;
(20) History of alcohol and/or drug abuse within the past 3 months prior to screening;
(21) Individuals with any conditions that may affect drug absorption, including but not limited to: malabsorption syndrome, celiac disease, gastrectomy, and intestinal resection (excluding appendectomy);
(22) Those who have used CYP3A strong inducers or inhibitors within 4 weeks or 5 half lives (whichever is longer) before the first administration, or who cannot avoid using CYP3A strong inducers or inhibitors during the study period (see Appendix 7);
(23) Those who consumed St. John's wort (Forsythia suspensa) products or grapefruit within 7 days prior to the first administration, or refused to avoid such substances throughout the entire study period (including follow-up);
(24) Select individuals who have donated blood or lost ≥ 400mL of blood within the previous 3 months or plan to donate blood during the study period;
(25) Individuals who are known or suspected to be allergic to any component of the investigational drug, or to any other significant drug allergy (such as anaphylactic shock or hepatotoxicity);
(26) Pregnant or lactating women;
(27) Those who use other clinical trial drugs or are currently participating in other clinical studies within 3 months or 5 half lives before the first administration (whichever is longer);
(28) Other circumstances that the researcher deems unsuitable for participation in this clinical study.研究实施时间:
Study execute time:
从
From
2025-12-29 00:00:00至
To
2026-12-31 00:00:00
征募观察对象时间:
Recruiting time:
从
From
2026-03-06 00:00:00
至
To
2026-12-31 00:00:00干预措施:
Interventions:
组别:
50mg QD组
样本量:
40
Group:
50mg QD group
Sample size:
干预措施:
空腹口服给药,每日服药一次,持续服药 12 周。
干预措施代码:
Intervention:
Take the medication on an empty stomach, once a day, for a duration of 12 weeks.
Intervention code:
组别:
100mg QD 组
样本量:
40
Group:
100mg QD group
Sample size:
干预措施:
空腹口服给药,每日服药一次,持续服药 12 周。
干预措施代码:
Intervention:
Take the medication on an empty stomach, once a day, for a duration of 12 weeks.
Intervention code:
组别:
200mg QD组
样本量:
40
Group:
200mg QD group
Sample size:
干预措施:
空腹口服给药,每日服药一次,持续服药 12 周。
干预措施代码:
Intervention:
Take the medication on an empty stomach, once a day, for a duration of 12 weeks.
Intervention code:
组别:
安慰剂组
样本量:
40
Group:
Placebo
Sample size:
干预措施:
空腹口服给药,每日服药一次,持续服药 12 周。
干预措施代码:
Intervention:
Take the medication on an empty stomach, once a day, for a duration of 12 weeks.
Intervention code:研究实施地点:
Countries of recruitment and research settings:
国家:
中国
省(直辖市):
北京
市(区县):
Country:
China
Province:
Beijing
City:
单位(医院):
中日友好医院
单位级别:
三甲
Institution
hospital:
China-Japan Friendship Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
广东
市(区县):
Country:
China
Province:
Guangdong
City:
单位(医院):
南方医科大学皮肤病医院
单位级别:
三甲
Institution
hospital:
Southern Medical University Dermatology Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
上海
市(区县):
Country:
China
Province:
Shanghai
City:
单位(医院):
上海市皮肤病医院
单位级别:
三甲
Institution
hospital:
Shanghai Skin Disease Hospita
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
湖北
市(区县):
Country:
China
Province:
Hubei
City:
单位(医院):
武汉市第一医院
单位级别:
三甲
Institution
hospital:
Wuhan First Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
浙江
市(区县):
Country:
China
Province:
Zhejiang
City:
单位(医院):
杭州市第一人民医院
单位级别:
三甲
Institution
hospital:
Hangzhou First People's Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
浙江
市(区县):
Country:
China
Province:
Zhejiang
City:
单位(医院):
浙江省人民医院
单位级别:
三甲
Institution
hospital:
Zhejiang Provincial People's Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
四川
市(区县):
Country:
China
Province:
Sichuan
City:
单位(医院):
四川省人民医院
单位级别:
三甲
Institution
hospital:
Sichuan Provincial People's Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
河北
市(区县):
Country:
China
Province:
Hebei
City:
单位(医院):
河北医科大学第二医院
单位级别:
三甲
Institution
hospital:
The Second Hospital of Hebei Medical University
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
广东
市(区县):
Country:
China
Province:
Guangdong
City:
单位(医院):
北京大学深圳医院
单位级别:
三甲
Institution
hospital:
Peking University Shenzhen Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
宁夏回族自治区
市(区县):
Country:
China
Province:
Ningxia Hui Autonomous Region
City:
单位(医院):
宁夏医科大学总医院
单位级别:
三甲
Institution
hospital:
General Hospital of Ningxia Medical University
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
海南
市(区县):
Country:
China
Province:
Hainan
City:
单位(医院):
海南省第五人民医院
单位级别:
三甲
Institution
hospital:
Hainan Provincial Fifth People's Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
江苏
市(区县):
Country:
China
Province:
Jiangsu
City:
单位(医院):
江苏大学附属医院
单位级别:
三甲
Institution
hospital:
Affiliated Hospital of Jiangsu University
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
河南
市(区县):
Country:
China
Province:
Henan
City:
单位(医院):
郑州市中心医院
单位级别:
三甲
Institution
hospital:
Zhengzhou Central Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
浙江
市(区县):
Country:
China
Province:
Zhejiang
City:
单位(医院):
杭州市第三人民医院
单位级别:
三甲
Institution
hospital:
Hangzhou Third People's Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
天津
市(区县):
Country:
China
Province:
Tianjin
City:
单位(医院):
天津医科大学总医院
单位级别:
三甲
Institution
hospital:
General Hospital of Tianjin Medical University
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
北京
市(区县):
Country:
China
Province:
Beijing
City:
单位(医院):
首都医科大学附属北京同仁医院
单位级别:
三甲
Institution
hospital:
Beijing Tongren Hospital, Capital Medical University
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
山东
市(区县):
Country:
China
Province:
Shandong
City:
单位(医院):
山东大学齐鲁医院
单位级别:
三甲
Institution
hospital:
Qilu Hospital of Shandong University
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
四川
市(区县):
Country:
China
Province:
Sichuan
City:
单位(医院):
四川大学华西医院
单位级别:
三甲
Institution
hospital:
West China Hospital, Sichuan University
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
辽宁
市(区县):
Country:
China
Province:
Liaoning
City:
单位(医院):
沈阳市中西医结合医院
单位级别:
三甲
Institution
hospital:
Shenyang Integrated Traditional Chinese and Western Medicine Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
辽宁
市(区县):
Country:
China
Province:
Liaoning
City:
单位(医院):
沈阳医学院附属中心医院
单位级别:
三甲
Institution
hospital:
Central Hospital Affiliated to Shenyang Medical College
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
福建
市(区县):
Country:
China
Province:
Fujian
City:
单位(医院):
福建医科大学附属第一医院
单位级别:
三甲
Institution
hospital:
The First Affiliated Hospital of Fujian Medical University
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
陕西
市(区县):
Country:
China
Province:
Shaanxi
City:
单位(医院):
陕西省人民医院
单位级别:
三甲
Institution
hospital:
Shaanxi Provincial People's Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
山东
市(区县):
Country:
China
Province:
Shandong
City:
单位(医院):
滨州医学院附属医院
单位级别:
三甲
Institution
hospital:
Affiliated Hospital of Binzhou Medical University
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
河北
市(区县):
Country:
China
Province:
Hebei
City:
单位(医院):
华北理工大学附属医院
单位级别:
三甲
Institution
hospital:
Affiliated Hospital of North China University of Science and Technology
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
江苏
市(区县):
Country:
China
Province:
Jiangsu
City:
单位(医院):
苏州市立医院
单位级别:
三甲
Institution
hospital:
Suzhou Municipal Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
湖北
市(区县):
Country:
China
Province:
Hubei
City:
单位(医院):
十堰市人民医院
单位级别:
三甲
Institution
hospital:
Shiyan People's Hospital
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
上海
市(区县):
Country:
China
Province:
Shanghai
City:
单位(医院):
上海中医药大学附属岳阳中西医结合医院
单位级别:
三甲
Institution
hospital:
Yueyang Hospital of Integrated Traditional Chinese and Western Medicine, Shanghai University of Traditional Chinese Medicine
Level of the institution:
Tertiary A
国家:
中国
省(直辖市):
北京
市(区县):
Country:
China
Province:
Beijing
City:
单位(医院):
北京怀柔医院
单位级别:
三甲
Institution
hospital:
Beijing Huairou Hospital
Level of the institution:
Tertiary A测量指标:
Outcomes:
指标中文名:
湿疹面积和严重程度指数较基线改善至少75%(EASI 75)的参与者比例
指标类型:
主要指标
Outcome:
Proportion of participants with at least 75% improvement from baseline in the Eczema Area and Severity Index (EASI 75)
Type:
Primary indicator
测量时间点:
第12周
测量方法:
Measure time point of outcome:
Week 12
Measure method:
指标中文名:
湿疹面积和严重程度指数较基线改善至少75%(EASI 75)的参与者比例
指标类型:
次要指标
Outcome:
The proportion of participants whose eczema area and severity index improved by at least 75% compared to baseline (EASI 75)
Type:
Secondary indicator
测量时间点:
第2、4、8周
测量方法:
Measure time point of outcome:
At weeks 2, 4, and 8
Measure method:
指标中文名:
达到EASI 50/90的参与者比例
指标类型:
次要指标
Outcome:
Proportion of participants reaching EASI 50/90
Type:
Secondary indicator
测量时间点:
第2、4、8、12周
测量方法:
Measure time point of outcome:
At weeks 2, 4, 8, and 12
Measure method:
指标中文名:
达到IGA 0或1分且较基线改善≥2分的参与者比例
指标类型:
次要指标
Outcome:
The proportion of participants who achieved IGA score of 0 or 1 and improved by >= 2 points from baseline
Type:
Secondary indicator
测量时间点:
第2、4、8、12周
测量方法:
Measure time point of outcome:
At weeks 2, 4, 8, and 12
Measure method:
指标中文名:
达到IGA 0分或1分的参与者比例
指标类型:
次要指标
Outcome:
The proportion of participants who achieved 0 or 1 IGA score
Type:
Secondary indicator
测量时间点:
第2、4、8、12周
测量方法:
Measure time point of outcome:
At weeks 2, 4, 8, and 12
Measure method:
指标中文名:
Itch NRS评分较基线改善≥4分的参与者比例
指标类型:
次要指标
Outcome:
The proportion of participants whose Itch NRS scores improved by >= 4 points from baseline
Type:
Secondary indicator
测量时间点:
第2、4、8、12周
测量方法:
Measure time point of outcome:
At weeks 2, 4, 8, and 12
Measure method:
指标中文名:
EASI评分较基线的百分比变化
指标类型:
次要指标
Outcome:
Percentage change in EASI score compared to baseline
Type:
Secondary indicator
测量时间点:
第2、4、8、12周
测量方法:
Measure time point of outcome:
At weeks 2, 4, 8, and 12
Measure method:
指标中文名:
SCORAD评分较基线的百分比变化
指标类型:
次要指标
Outcome:
Percentage change in SCORAD score compared to baseline
Type:
Secondary indicator
测量时间点:
第2、4、8、12周
测量方法:
Measure time point of outcome:
At weeks 2, 4, 8, and 12
Measure method:
指标中文名:
Itch NRS评分较基线的变化
指标类型:
次要指标
Outcome:
Changes in Itch NRS score compared to baseline
Type:
Secondary indicator
测量时间点:
第2、4、8、12周
测量方法:
Measure time point of outcome:
At weeks 2, 4, 8, and 12
Measure method:
指标中文名:
受累体表面积(BSA)较基线的百分比变化
指标类型:
次要指标
Outcome:
Percentage changes in affected body surface area (BSA) compared to baseline
Type:
Secondary indicator
测量时间点:
第2、4、8、12周
测量方法:
Measure time point of outcome:
At weeks 2, 4, 8, and 12
Measure method:
指标中文名:
皮肤病学生活质量指数(DLQI)评分较基线的变化
指标类型:
次要指标
Outcome:
Changes in Dermatology Quality of Life Index (DLQI) scores from baseline
Type:
Secondary indicator
测量时间点:
第2、4、8、12周
测量方法:
Measure time point of outcome:
At weeks 2, 4, 8, and 12
Measure method:
指标中文名:
不良事件、实验室检查、生命体征、心电图检查、体格检查等
指标类型:
附加指标
Outcome:
Adverse events, laboratory tests, vital signs, electrocardiogram examination, physical examination, etc
Type:
Additional indicator
测量时间点:
测量方法:
Measure time point of outcome:
Measure method:
指标中文名:
评价CMS-D001及其主要代谢产物(如适用)在中重度特应性皮炎参与者中的PK特征
指标类型:
附加指标
Outcome:
Evaluate the PK characteristics of CMS-D001 and its major metabolites (if applicable) in participants with moderate to severe atopic dermatitis
Type:
Additional indicator
测量时间点:
测量方法:
Measure time point of outcome:
Measure method:
指标中文名:
群体药代动力学(PopPK)分析
指标类型:
附加指标
Outcome:
Population pharmacokinetic (PopPK) analysis
Type:
Additional indicator
测量时间点:
测量方法:
Measure time point of outcome:
Measure method:
指标中文名:
暴露-效应分析:CMS-D001及其主要代谢产物(如适用)的暴露与疗效和不良事件之间的关系
指标类型:
附加指标
Outcome:
Exposure effect analysis: The relationship between exposure to CMS-D001 and its major metabolites (if applicable) and efficacy and adverse events
Type:
Additional indicator
测量时间点:
测量方法:
Measure time point of outcome:
Measure method:
指标中文名:
评价血清胸腺活化调节趋化因子(TARC)和免疫球蛋白E(IgE)等生物标志物水平及其较基线变化随时间的变化
指标类型:
附加指标
Outcome:
Evaluate the levels of biomarkers such as serum thymic activation regulatory chemokine (TARC) and immunoglobulin E (IgE) and their changes over time compared to baseline
Type:
Additional indicator
测量时间点:
测量方法:
Measure time point of outcome:
Measure method:采集人体标本:
Collecting sample(s)
from participants:
标本中文名:
血液
组织:
无
Sample Name:
Blood
Tissue:
None
人体标本去向
使用后销毁
说明
无
Fate of sample:
Destruction after use
Note:
None征募研究对象情况:
Recruiting status:
尚未开始
Not yet
recruiting
年龄范围:
Participant age:
最小
Min age
18
岁
years
最大
Max age
75
岁
years性别:
男女均可
Gender:
Both随机方法(请说明由何人用什么方法产生随机序列):
本研究采用分层区组随机化方法,参与者的基线IGA评分(3分或4分)将作为随机分层因子,在每层内参与者将按照1:1:1:1比例随机分配至CMS-D001 50mg QD剂量组、100mg QD剂量组、200mg QD剂量组和安慰剂组。随机化将采用网络应答系统(IWRS)进行,该系统按照随机化编号自动随机分配治疗组。经过合适包装的研究药物,可一次或分若干次提供给研究中心。对符合纳入条件的参与者,将根据参与者的随机号,匹配对应的药物编号,分配药物。已完成随机的参与者,如果终止治疗或退出研究,无论其是否使用试验用药品、因任何原因终止治疗或退出研究,其随机号都不能分配给其他参与者再次使用。Randomization Procedure (please state who
generates the
random number sequence and by what method):
This study used a stratified block randomization method, where participants' baseline IGA scores (3 or 4 points) were used as random stratification factors. Within each layer, participants were randomly assigned to CMS-D001 50mg QD dose group, 100mg QD dose group, 200mg QD dose group, and placebo group in a 1:1:1:1 ratio. Randomization will be conducted using an Internet of Response System (IWRS), which automatically assigns treatment groups based on randomization numbers. The research drug, packaged appropriately, can be provided to the research center in one or several portions. For participants who meet the inclusion criteria, corresponding drug numbers will be matched based on their random numbers and drugs will be assigned. Participants who have completed randomization and terminate treatment or withdraw from the study, regardless of whether they use the investigational drug or terminate treatment or withdraw from the study for any reason, their randomization number cannot be assigned to other participants for reuse.是否公开试验完成后的统计结果:
Calculated Results after the Study Completed public access:
不公开/Private盲法:
盲法可确保研究评估不受具体治疗分配的影响。本研究采用双盲设计,即研究治疗过程中参与者、研究者均不清楚随机分组治疗分配情况。Blinding:
Blinding ensures that the research evaluation is not affected by specific treatment allocation. This study uses a double-blind design, meaning that neither the participants nor the researchers are aware of the random group treatment allocation during the treatment process.是否共享原始数据:
IPD sharing
否No共享原始数据的方式(说明:请填入公开原始数据日期和方式,如采用网络平台,需填该网络平台名称和网址):
无The way of sharing IPD”(include metadata and
protocol,
If use web-based public database, please provide
the
url):
None数据采集和管理(说明:数据采集和管理由两部分组成,一为病例记录表(Case
Record Form, CRF),二为电子采集和管理系统(Electronic Data
Capture, EDC),如ResMan即为一种基于互联网的EDC:
电子采集和管理系统Data collection and Management (A
standard data collection and management system
include a CRF and an electronic data capture:
Electronic Data Capture, EDC数据与安全监察委员会:
Data and Safety Monitoring Committee:
无/No注册人:
Name of Registration:
2026-02-25 09:33:15
临床2期
100 项与 Nicotinamide riboside/Pterostilbene 相关的药物交易
登录后查看更多信息
研发状态
10 条进展最快的记录, 后查看更多信息
登录
| 适应症 | 最高研发状态 | 国家/地区 | 公司 | 日期 |
|---|---|---|---|---|
| 急性肾损伤 | 临床2期 | 美国 | 2020-12-01 | |
| 腹主动脉瘤 | 临床2期 | 美国 | 2020-12-01 | |
| 胸主动脉瘤 | 临床2期 | 美国 | 2020-12-01 | |
| 肌萎缩侧索硬化 | 临床1期 | 欧洲 | - | |
| 更年期综合症 | 临床阶段不明 | 美国 | 2021-04-05 |
登录后查看更多信息
临床结果
临床结果
适应症
分期
评价
查看全部结果
| 研究 | 分期 | 人群特征 | 评价人数 | 分组 | 结果 | 评价 | 发布日期 |
|---|
No Data | |||||||
登录后查看更多信息
转化医学
使用我们的转化医学数据加速您的研究。
登录
或
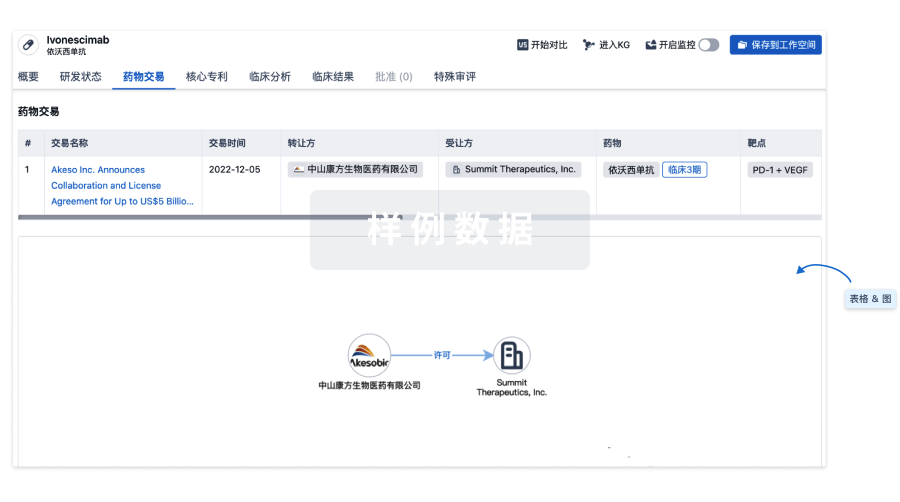
药物交易
使用我们的药物交易数据加速您的研究。
登录
或
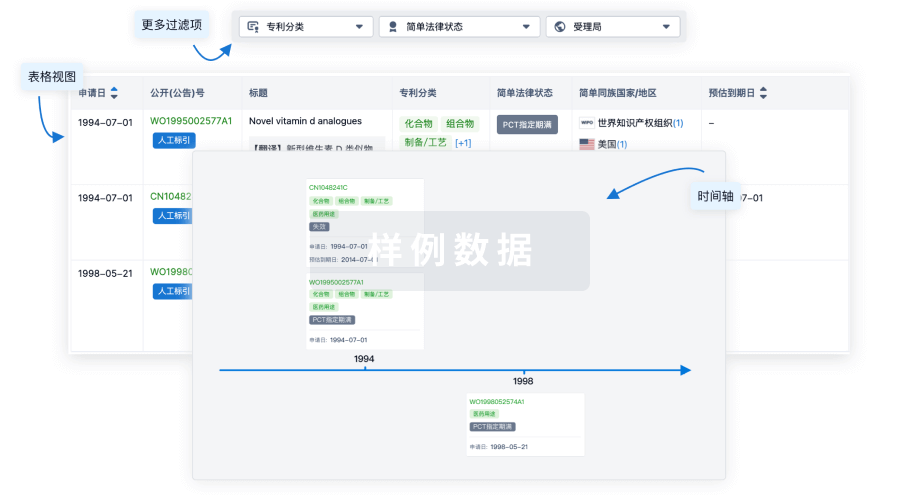
核心专利
使用我们的核心专利数据促进您的研究。
登录
或
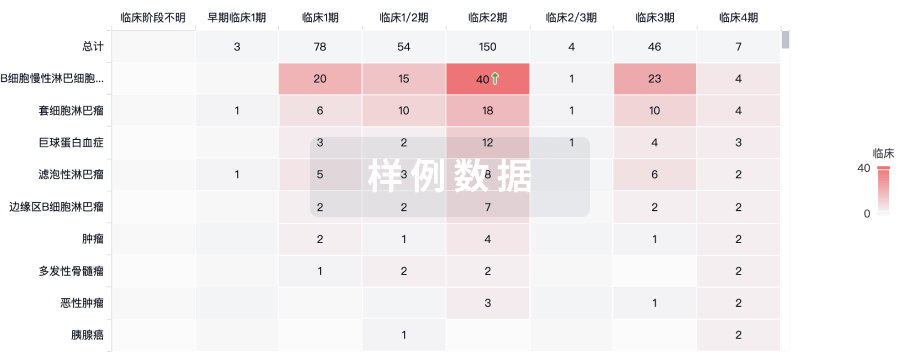
临床分析
紧跟全球注册中心的最新临床试验。
登录
或
批准
利用最新的监管批准信息加速您的研究。
登录
或
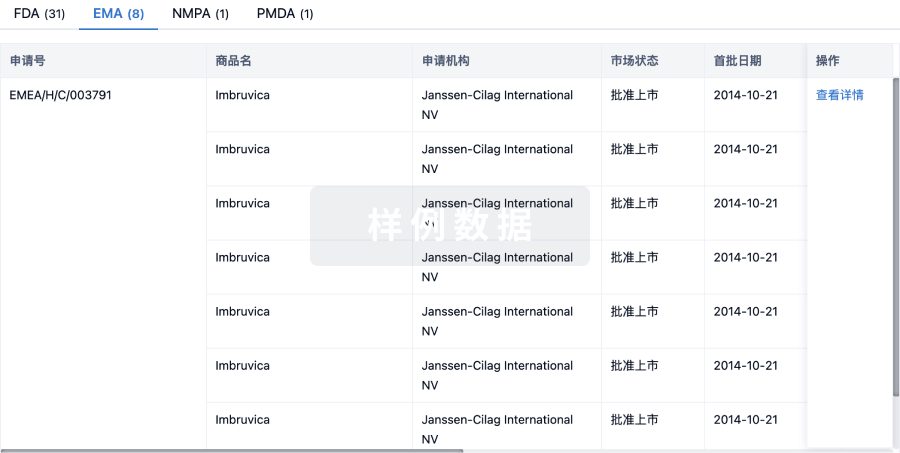
特殊审评
只需点击几下即可了解关键药物信息。
登录
或
生物医药百科问答
全新生物医药AI Agent 覆盖科研全链路,让突破性发现快人一步
立即开始免费试用!
智慧芽新药情报库是智慧芽专为生命科学人士构建的基于AI的创新药情报平台,助您全方位提升您的研发与决策效率。
立即开始数据试用!
智慧芽新药库数据也通过智慧芽数据服务平台,以API或者数据包形式对外开放,助您更加充分利用智慧芽新药情报信息。
生物序列数据库
生物药研发创新
免费使用
化学结构数据库
小分子化药研发创新
免费使用



