预约演示
更新于:2025-12-25

Brown University
更新于:2025-12-25
概览
标签
肿瘤
消化系统疾病
其他疾病
小分子化药
治疗性疫苗
自然杀伤细胞疗法
疾病领域得分
一眼洞穿机构专注的疾病领域
暂无数据
技术平台
公司药物应用最多的技术
暂无数据
靶点
公司最常开发的靶点
暂无数据
| 排名前五的药物类型 | 数量 |
|---|---|
| 小分子化药 | 12 |
| 自然杀伤细胞疗法 | 1 |
| 未知 | 1 |
| 治疗性疫苗 | 1 |
| 预防性疫苗 | 1 |
关联
17
项与 Brown University 相关的药物作用机制 Akt-1抑制剂 [+4] |
在研机构 |
原研机构 |
最高研发阶段批准上市 |
首次获批国家/地区 美国 |
首次获批日期2025-08-06 |
作用机制 CLPP激动剂 [+3] |
在研机构 |
最高研发阶段临床2期 |
首次获批国家/地区- |
首次获批日期- |
靶点 |
作用机制 GSK-3β抑制剂 |
最高研发阶段临床2期 |
首次获批国家/地区- |
首次获批日期- |
512
项与 Brown University 相关的临床试验NCT03313622
Locating Biomarkers of Medically Intractable Obsessive Compulsive Disorder (OCD) Through the Use of Behavioral Tasks
Subjects that have a diagnosis of OCD will participate in a clinical interview and cognitive tasks, during which they will be exposed to their individual OC stressors or will be asked to make decisions related to information value and quantity while measuring neural activity and filming facial reactions. This will assist investigators to look for biomarkers of that change. This study offers a unique opportunity to develop biomarkers for key domains of OCD, and other neuropsychiatric disorders, that are grounded in brain neurocircuitry at the individual-patient level.
Subjects will participate in a clinical interview (Day 1), and then tasks+EEG (Day 2). Day 1 will be 4 hours or less, and Day 2 will be 2.5 hours or less.
Subjects will participate in a clinical interview (Day 1), and then tasks+EEG (Day 2). Day 1 will be 4 hours or less, and Day 2 will be 2.5 hours or less.
开始日期2026-03-01 |
申办/合作机构 |
NCT07099638
Randomized Factorial Trial of Varenicline With Nicotine Lozenges and a Smartphone Medication Adherence Intervention to Promote Smoking Cessation
Although the prevalence of smoking has declined among U.S. adults, smoking remains the leading preventable cause of cancer incidence and mortality. Quitting smoking increases life expectancy, and quitting at an earlier age is associated with more years of life gained. Effective pharmacotherapies to aid cessation are available, and the combination of behavioral support with pharmacotherapy optimizes cessation outcomes. Varenicline is an effective, first-line smoking cessation treatment, and recent research has investigated combination pharmacotherapy to improve the modest quit rates observed with monotherapy. The findings of two meta-analyses have indicated that varenicline combined with the nicotine patch was more effective than varenicline alone for smoking cessation However, no published studies to date have evaluated the combined impact of varenicline and oral nicotine replacement therapy (NRT) on smoking cessation in a randomized trial. Oral NRT, such as nicotine lozenges, can provide acute relief from cravings/withdrawal, and offers individuals the flexibility to deliver nicotine quickly, in contrast with the continuous, passive, and slow-acting delivery of the nicotine patch. Nevertheless, in clinical trials of other combination pharmacotherapies, participants' adherence to of oral NRT has been suboptimal, making it difficult to determine whether there is an added benefit. Given the near-ubiquity of smartphone ownership (85% of U.S. adults), it is plausible that smartphone-based medication adherence interventions could have a positive influence on pharmacotherapy adherence and smoking cessation. This investigative team has demonstrated the feasibility and potential efficacy of using combination varenicline plus oral NRT treatment to promote smoking cessation in a pilot factorial randomized trial. Likewise, pilot findings showed that medication adherence and smoking cessation rates were higher among those who received smartphone-based medication reminders than those who did not. The proposed study will enroll 496 adults who smoke cigarettes daily. The study will employ a 2x2 factorial design in which participants will be randomized to one of four combinations of two treatment factors: 1) pharmacological treatment (varenicline + nicotine lozenges vs. varenicline alone) and 2) smartphone medication adherence intervention (smartphone-based smoking cessation app with vs. without adherence components). The primary study outcomes will be biochemically-confirmed 7-day point prevalence abstinence at 26 weeks after a scheduled quit date, and medication adherence over the 13-week treatment period. Smartphone-based daily diaries will be employed to assess daily smoking and medication adherence. Notably, the proposed study will employ entirely remote assessment and treatment delivery strategies. Exploratory analyses will evaluate the potential interaction between medication type and the smartphone adherence intervention, and compare the influences of pharmacological treatment type and the medication adherence intervention on weekly physical symptoms (e.g., withdrawal, medication side effects). The overarching goal of the proposed research is to improve smoking cessation treatment and decrease cancer risk.
开始日期2026-01-05 |
申办/合作机构 |
NCT05901766
Effect of Maternal Supplementation With an Iodine-containing Multiple Micronutrient During Lactation on Infant Iodine Status, Thyroid Function and Neurodevelopment
The goal of this clinical trial is to learn about the effects of iodine-containing multiple micronutrient supplements provided to breastfeeding mothers who live in settings with mild iodine deficiency.
The main questions it aims to answer are:
1. What are the effects of iodine-containing multiple micronutrient supplements provided to breastfeeding mothers on infant development, as measured by electroencephalography/visual evoked potentials?
2. What are the effects of iodine-containing multiple micronutrient supplements on breast milk concentrations of iodine, and infant iodine and thyroid status?
3. How do iodine and iron interact with each other to affect thyroid function in the mother during lactation?
Participants will be randomized to receive a daily multiple micronutrient tablet containing iodine (UNIMAPP) for 6 months postpartum, or routine postnatal care per Ethiopia Ministry of Health. Mothers will provide a breast milk sample and blood at 3 and 6 months postpartum. Infants will provide a urine sample and drop of blood, and have a neurodevelopmental assessment at 3 and 6 months.
Researchers will compare the groups that received the iodine-containing micronutrient supplement with the group that received routine care and see if there were any benefits on infant development and iodine and thyroid status in the mother and baby.
The main questions it aims to answer are:
1. What are the effects of iodine-containing multiple micronutrient supplements provided to breastfeeding mothers on infant development, as measured by electroencephalography/visual evoked potentials?
2. What are the effects of iodine-containing multiple micronutrient supplements on breast milk concentrations of iodine, and infant iodine and thyroid status?
3. How do iodine and iron interact with each other to affect thyroid function in the mother during lactation?
Participants will be randomized to receive a daily multiple micronutrient tablet containing iodine (UNIMAPP) for 6 months postpartum, or routine postnatal care per Ethiopia Ministry of Health. Mothers will provide a breast milk sample and blood at 3 and 6 months postpartum. Infants will provide a urine sample and drop of blood, and have a neurodevelopmental assessment at 3 and 6 months.
Researchers will compare the groups that received the iodine-containing micronutrient supplement with the group that received routine care and see if there were any benefits on infant development and iodine and thyroid status in the mother and baby.
开始日期2026-01-01 |
申办/合作机构  Brown University Brown University [+4] |
100 项与 Brown University 相关的临床结果
登录后查看更多信息
0 项与 Brown University 相关的专利(医药)
登录后查看更多信息
42,297
项与 Brown University 相关的文献(医药)2026-12-01·Nano-Micro Letters
Radiative Coupled Evaporation Cooling Hydrogel for Above-Ambient Heat Dissipation and Flame Retardancy
Article
作者: Shi, Changming ; Ye, Qin ; Chen, Meijie ; Sheldon, Brian W ; Yao, Baojian ; Huang, Yimou ; Chen, Zhuo
Abstract:
By combining the merits of radiative cooling (RC) and evaporation cooling (EC), radiative coupled evaporative cooling (REC) has attracted considerable attention for sub-ambient cooling purposes. However, for outdoor devices, the interior heating power would increase the working temperature and fire risk, which would suppress their above-ambient heat dissipation capabilities and passive water cycle properties. In this work, we introduced a REC design based on an all-in-one photonic hydrogel for above-ambient heat dissipation and flame retardancy. Unlike conventional design RC film for heat dissipation with limited cooling power and fire risk, REC hydrogel can greatly improve the heat dissipation performance in the daytime with a high workload, indicating a 12.0 °C lower temperature than the RC film under the same conditions in the outdoor experiment. In the nighttime with a low workload, RC-assisted adsorption can improve atmospheric water harvesting to ensure EC in the daytime. In addition, our REC hydrogel significantly enhanced flame retardancy by absorbing heat without a corresponding temperature rise, thus mitigating fire risks. Thus, our design shows a promising solution for the thermal management of outdoor devices, delivering outstanding performance in both heat dissipation and flame retardancy.
2026-04-01·BIOMATERIALS
A coordinated biomaterial strategy for post-infarction cardiac repair: integrating tailored mechanical reinforcement with hiPSC-derived cardiomyocytes in composite engineered human myocardium for remuscularization
Article
作者: Callanan, Anthony ; Dwyer, Kiera D ; Snyder, Caroline A ; Coulombe, Kareen L K ; Soepriatna, Arvin H
Up to 1 billion cardiomyocytes (CMs) die during myocardial infarction (MI), leading to permanent muscle loss and devasting functional impacts. Biomaterial therapies have aimed to passively reinforce the infarcted left ventricle (LV), but their therapeutic impact remains limited as they fail to directly address the loss of functional CMs. In this work, we employed a simulation-guided workflow to design an optimized biomaterial support that can be combined with contractile CMs for implantation after MI. A finite element model (FEM) of the LV post-MI was developed and showed longitudinal reinforcement and active contractility improves ejection fraction (EF) post-MI (+3.39 % and +14.97 %, respectively). To this end, we developed a coordinated remuscularization-reinforcement therapy using engineered human myocardium (EHM) composed of human induced pluripotent stem cell-derived CMs (hiPSC-CMs) integrated with a highly aligned electrospun polycaprolactone (PCL) scaffold. Remuscularization (EHM-only), reinforcement (PCL-only) and its coordinated therapy (PCL-EHM) were evaluated in a rat model of MI. We report successful engraftment of the implants onto the heart with significant maturation of hiPSC-CMs after four weeks in vivo (∼7-fold increase of cTnT area and ∼2-fold increase MLC2v area compared to in vitro cultured controls). Using 4D ultrasound (US), we quantified 3D regional strains and found that the benefits of PCL reinforcement on maintaining LV structure and function were additive with remuscularization by EHM. This additive effect was reflected inimproved regional strain after injury when PCL and EHM were delivered as a composite therapy. This work establishes a promising strategy for synergistic reinforcement and remuscularization of the infarcted heart.
2026-03-01·JOURNAL OF AFFECTIVE DISORDERS
Neighborhood socioeconomic disadvantage and antenatal depressive symptoms
Article
作者: Saade, George ; Simhan, Hyagriv ; Venkatesh, Kartik K ; Chung, Judith ; Wu, Jiqiang ; Pippen, Jessica ; Parry, Samuel ; Grobman, William A ; Wu, Jun ; Miller, Michelle L ; Lammers, Sydney ; Reddy, Uma M ; Silver, Robert M ; Yee, Lynn M ; McNeil, Becky ; Lynch, Courtney D
BACKGROUND:
We evaluated whether neighborhood-level socioeconomic disadvantage was associated with mid-pregnancy antenatal depressive symptoms.
METHODS:
We conducted a secondary analysis of data from the Nulliparous Pregnancy Outcomes Study: Monitoring Mothers-To-Be, a prospective cohort of nulliparous pregnant individuals. The exposure was socioeconomic disadvantage by the Area Deprivation Index (ADI) categorized by tertile, with the least deprived tertile (T1) as the reference. The ADI was calculated per participant residential address in early pregnancy geocoded at the block group level. The outcome was depressive symptoms assessed between 22 and 29 weeks as a score ≥ 10 on the Edinburgh Postnatal Depression Scale (EPDS), and secondarily as a score ≥ 13. Multivariable modified Poisson regression was used and adjusted for age, individual-level social determinants of health, and the EPDS score in early pregnancy.
RESULTS:
Of 8678 nulliparous individuals, the median ADI score was 38.0 (interquartile range [IQR]: 18.0, 69.0). A total of 16.1 % of individuals had an EPDS score ≥ 10, and 6.5 % had an EPDS score ≥ 13 at a median gestational age of 26.9 weeks. Individuals who lived in a neighborhood with the highest tertile of ADI were more likely to have a score ≥ 10 compared with those in the lowest tertile (21.6 % vs. 11.7 %; adjusted risk ratio [aRR]: 1.29; 95 % CI: 1.12, 1.50). The association was similar at the higher EPDS screening threshold ≥13 (9.9 % vs. 3.8 %; aRR: 1.60; 95 % CI: 1.23, 2.09). These results held in sensitivity analyses, including without adjusting for the EPDS in early pregnancy, when adjusting for additional clinical characteristics, when analyzing the ADI in declines and as a continuous variable, and when analyzing the ADI per national tertile cutoffs.
CONCLUSIONS:
Neighborhood-level socioeconomic disadvantage was associated with an increased risk of screening positive for elevated antenatal depressive symptoms in mid-pregnancy.
396
项与 Brown University 相关的新闻(医药)2025-12-21
2025年8月20日中国工程院公布2025 年院士增选有效候选人 660 人名单,赤壁籍陈建国教授位列其中,他是赤壁市20年来唯一一位进入院士候选人的专家。2005年赤壁市曾出过一位院士候选人,此后20年再无人问鼎,所以家乡一直非常期待能有人打破这个“纪录”。
2025年9月25-28日,中国神经科学学会第十八届全国学术会议(CNS 2025)在西安隆重召开,参会签到人数4589人,海外专题比例超过65%,其中报告人约80人,来自美国、英国、德国、澳大利亚、加拿大、澳大利亚、韩国、日本近20个国家。陈建国教授应邀参加并做报告。
这次能够闯进院士候选人的陈建国教授,家乡人还是有些意外,因为他在家乡人印象中略显“陌生”,主要源于他从事的是基础医学教学与研究工作,与家乡互动不是很多。
2021年12月24日,华中科技大学副校长陈建国带队与清华大学副校长杨斌等围绕清华大学全球战略规划、国际化能力提升等议题进行交流。
陈建国教授为何能够成为院士候选人,他有着怎样的卓越成就和家国情怀?
在华中科技大学同济医学院的历史长河中,陈建国教授的名字镌刻着卓越与担当。他曾担任十年华中科技大学党委常委、副校长,并兼任同济医学院党委书记、院长,以教育家的格局、科学家的严谨和医者的仁心,在医学教育改革、神经精神药理学研究及公共卫生实践中留下了深刻印记。他的人生轨迹,交织着个人奋斗与家国情怀,书写了一部当代医学教育者的励志篇章。
2022年9月14日,浙江大学智能创新药物研究院主办金沙论坛系列讲座。特邀陈建国教授做题为《老药新发现:基于转化理念的抗抑郁症药物研究》的学术讲座。
求学之路:从鄂南小城到国际学术舞台
陈建国教授1963年出生于湖北赤壁,这座鄂南小城的山水赋予了他坚韧不拔的性格。1980年,他以优异成绩考入咸宁医学院临床医学专业,开启了医学之路。本科期间,他不仅系统学习医学知识,更在图书馆的浩瀚书海中埋下了科研的种子。
2025年11月8日,湖北科技学院咸宁医学院办学60周年“校友回归”暨创新发展大会隆重召开。杰出校友陈建国教授应邀出席并作《坚持以学生为中心,夯实新医科建设》主题报告。
1987年,他考入同济医科大学攻读生理学硕士学位,师从著名生理学家李之望教授。1990年作为优秀的毕业生留校在药理学系任教。在同济医科大学学习和工作期间,逐渐发现了药理学的独特魅力——这门学科像一座桥,贯通基础医学与临床实践,更承载着新药研发的使命。“药理学的本质是‘格药穷理’。”他说道。
1995年,陈建国教授获得德国自然科学基金项目资助,赴德国凯泽斯劳滕大学进修,师从著名生物学家约翰•戴德曼教授从事星形胶质细胞研究,后转入海德堡大学攻读博士,师从著名神经科学家约根•萨迪库勒教授从事疼痛原理与镇痛药的研究,于1998年获得海德堡大学医学博士学位。
三年多的留德经历不仅提升了他的学术视野,更让他深刻认识到国际合作对科研突破的重要性。随后,他于1998-2021期间,在美国爱荷华大学医学院从事博士后研究,师从著名的离子通道电生理学家托西•荷西教授,在神经科学与分子药理学的研究方面做出了卓越成绩。
六年多的海外生涯,他辗转欧美顶尖实验室,不仅积累了丰富的科研经验,更深刻体会到国际前沿的学术理念与研究方法。然而,尽管国外的科研条件优越,他始终怀揣着对祖国的思念与责任感。在他心中,同济医科大学不仅是他学术生涯的起点,更是他心中永远的牵挂。
2023年11月4日,2023国际产学研用合作会议(湖北)开幕式在华中科技大学成功举办。在开幕式揭牌仪式环节,副校长陈建国教授和欧洲科学院及德国科学院院士、法兰克福大学医学院分子医学中心主任兼血管信号研究所所长Ingrid Fleming教授共同为“中德心肺科学实验室”揭牌。
学术成就:解码大脑奥秘的科研先锋
2002年,陈建国教授放弃国外优渥条件,毅然归国,回到刚刚完成学校合并的华中科技大学同济医学院担任药理学系教授、系主任,一干就是二十多年。陈建国教授全身心投入神经精神药理学教学与研究,尤其关注抑郁症、焦虑症和药物成瘾等重大疾病的发病机制和治疗药物。
他带领团队在《Nature Metabolism》、《Cell Metabolism》等国际顶级期刊发表系列论文,揭示了抑郁症发病新机制,提出了新的理论学说,发现了新的治疗药物。例如,2023年他与团队发现,慢性应激通过激活Drp1蛋白导致神经元线粒体功能障碍,而抑制Drp1可显著改善抑郁症状,这一成果为抑郁症治疗提供了新靶点。
华中科技大学同济医学院药理学系
作为首席科学家,他先后主持多项国家级重大重点科研计划项目,包括国家973计划、国家脑计划、国家重大新药创制专项、国家自然科学基金创新群体等项目,在衰老相关认知障碍、情绪障碍性疾病的发病机制与药物干预等领域取得系统性创新成果。
他构建的动物模型和分子机制研究,为理解神经精神疾病的病理过程提供了重要理论支撑。同时,他注重成果转化,推动多项研究成果进入临床研究阶段,为新药研发奠定基础。 相关科研成果获得教育部自然科学一等奖、湖北省自然科学一等奖(2项)等。
同时他本人也获得国家杰出青年基金、教育部长江学者特聘教授、享受国务院政府特殊津贴专家、湖北省医学领军人才等多项人才计划的资助。作为归侨,他还获得中国侨界(创新人才)贡献奖和湖北省梁亮胜侨界科技奖励二等奖等。
2019年11月7日,华中科技大学与美国韦恩州立大学 “国际妇女健康研究项目”合作协议在同济医学院正式签署。韦恩州立大学医学院副院长Marcus Zervos教授和华中科技大学党委常委、副校长,同济医学院党委书记、院长陈建国教授等出席。
教育改革:塑造医学人才培养新范式
2015-2024年期间,陈建国教授担任华中科技大学副校长兼同济医学院党委书记、院长,开启了医学教育改革的新篇章。他提出“大健康、群健康、同健康、全健康”的“四维健康”新理念,强调医学教育要从疾病治疗转向疾病预防和健康促进。
在他的推动下,华中科技大学深化“医工结合”“医理交叉”,如组织专家团队与华为合作开发人工智能辅助诊断系统,在新冠肺炎疫情期间发挥了重要作用。
他参与建设国际教育科技创新园区(军山校区),引入数字化管理和国际化课程体系,打造跨学科创新平台。此外,他积极推进“一院一校”国际合作战略,与英国伯明翰大学、德国海德堡大学等建立深度合作,开展人才联合培养和科研攻关。
陈建国教授指导研究生实验
在同济医学院的学科建设中,他亲自指导实验室建设,引进先进设备,培养年轻人才。在他的带领下,同济医学院的药理学学科得到了迅猛发展,在ESI国际学科排行榜中进入1‰的国际先进之列。
作为国家“十二五”、“十三五”规划教材《药理学》主编,陈建国教授致力于教学内容革新。他将最新科研成果融入教材,强调基础与临床结合,培养学生的批判性思维和创新能力。
他主编的《药理学》教材获国家优秀教材一等奖,主讲的《药理学》课程被评为国家级精品课程,指导的研究生多次获得国家奖学金和优秀学位论文奖。他作为第一完成人的教学成果获得国家教学成果二等奖,他本人也获得“宝钢优秀教师奖”,并入选国家级教学名师。
2020年11月9日,华中科技大学与德国杜伊斯堡-埃森大学联合举办第四届中德医学学术联合讲演会。副校长陈建国对德国疫情表达了关切,同时对双方在质子治疗领域深化合作表示期待。
家国情怀:在公共卫生战场彰显担当
2020年,新冠疫情突袭武汉,陈建国教授临危受命,担任华中科技大学疫情防控领导小组副组长、科研攻关领导小组组长。他迅速组织多学科团队开展应急研究,如推动协和医院侯晓华教授团队研发的IgM/IgG抗体快速检测试剂盒投入临床,15分钟即可出结果,有效弥补了核酸检测的不足。他提出“中西医并重”策略,力推附属同济医院将“金叶败毒颗粒”等临床应用有效的中药验方广泛应用于新冠疫情防控制之中。
疫情期间,他牵头建立“华中科技大学-湖北省红十字会应急救护培训基地”,培训专业救护人员数万人。他在《光明日报》发表署名文章《疫情下关于“新医科”的若干思考》,呼吁加强公共卫生体系建设和全球卫生治理合作,这一观点被纳入国家“十四五”医学教育改革规划。
此外,为了支持国际疫情防控,他还组织了70余场国际疫情防控视频交流会议,将我国的疫情防控成功经验与国外合作学校进行分享和交流,并接受国际著名杂志《科学》等的采访,正面介绍和宣传我国的疫情防控经验和成果,为国际疫情防控做出了重要贡献。
2023年6月20日-23日,2023泰晤士高等教育亚洲大学峰会(Times Higher Education Asia Universities Summit)在香港中文大学举行,华中科技大学副校长陈建国受邀率团参会,与来自世界知名高校领导与国际高等教育专家交流,共同探讨亚洲大学的发展与未来,并受邀参加主题研讨会。
国际视野:搭建医学交流的桥梁
陈建国始终秉持开放办学理念,推动华中科技大学融入全球教育体系。他率团访问美国的哈佛大学、布朗大学、芝加哥大学、爱荷华大学,英国的剑桥大学、曼彻斯特大学、伯明翰大学,德国的海德堡大学、慕尼黑大学、杜伊斯堡-埃森大学、马尔堡大学,法国的巴黎萨克雷大学、巴黎第五大学,新加坡国立大学、南洋理工大学,加拿大的麦吉尔大学等世界名校,签署多项合作协议,并与其中多所学校建立了全方位合作伙伴关系。
2019年7月11日,华中科技大学副校长陈建国(右)访问芝加哥大学,与芝加哥大学副校长尼瓦桑(Balaji Srinivasan) (左)交流。
启动“3+1+1”联合培养项目,每年选派数百名学生赴海外交流。并建成中外合作办学基地。他本人也获得英国伯明翰大学荣誉教授称号。
2023年3月27日-4月5日,华中科技大学副校长陈建国率团出访欧洲,先后访问法国巴黎萨克雷大学、巴黎高等矿业学校,英国伯明翰大学、伦敦玛丽女王大学,德国慕尼黑工业大学,共叙友谊、共商合作,巩固发展学校欧洲“朋友圈”,着力夯实全球伙伴网络布局。
薪火相传:西迁精神的传承人
作为同济人,陈建国教授对医学院三次西迁的故事如数家珍。
同济的第一次西迁是在艰苦的抗战年代搬迁到四川宜宾的李庄继续办学。他尤爱讲述老院长唐哲教授用芒硝救治当地居民钡中毒的往事,正所谓“成绩斐然,人民受益匪浅,颂声载道,令誉日隆”。
第二次西迁是建国初期,响应国家号召,同济大学医学院整体从上海搬迁至医疗卫生队伍极度缺乏的华中重镇—武汉,组建中南同济医学院,为国家特别是中部地区培养了大批杰出医药卫生人才,为我国在长江流域消灭血吸虫病这一严重影响人民健康的重大流行病作出了巨大贡献。
第三次西迁是上世纪六十年代中期,同济医学院(时名武汉医学院)再次响应国家 “把医疗工作的重点放到农村去”的伟大号召,派出精干力量,在地处鄂西北山区的十堰市组建“武汉医学院郧阳分院”,为缓解鄂西北地区缺医少药的困境作出了重大贡献。
三次西迁精神一脉相承,就是“国家的需要就是同济的追求”,同济就是“与祖国同舟,与人民共济”。这种精神是陈建国教授心中永恒的灯塔,在他身上也得到了传承:他坚持响应国家对口支援新疆的号召,全力支援新疆石河子大学医学院,在学科建设和人才培养方面给予了巨大的支持。
2025年10月27日-29日,湖北省教育厅“世界著名科学家来鄂讲学计划”支持、湖北医药学院主办的“创新药物概念验证国际论坛”在湖北十堰举办,陈建国教授作了题为“基于肠道菌群调控的抑郁症发病机制与干预药物研究”的报告。
全力支持郧阳医学院(现湖北医药学院)的建设与发展,在科研平台的组建、学术交流与合作、人才培养等方面给与了不遗余力的支持。他说,同济的“济”字,既是济世,更是共济,体现了浓郁的家国情怀。
陈建国教授始终坚信,同济医学院的未来在于不断创新与突破。他鼓励年轻一代要保持对科学的敬畏之心,勇于探索未知领域。在他的带领下,同济医学院的药理学团队正朝着国际一流的目标稳步迈进。
他希望每一位同济人都能牢记“同舟共济、格物穷理”的院训,以德为先,以医为本,为人类健康事业贡献自己的力量。
从赤壁小城出来的医学生到国际知名的医学教育家,陈建国教授用三十余载光阴诠释了“健康所系,性命相托”的誓言。他以科研突破探索生命奥秘,以教育改革培养医学栋梁,以公共卫生实践守护人民健康。
他的故事,是中国医学教育发展的缩影,更是一位知识分子家国情怀的生动写照。正如他在《药理学》教材前言中所言:“医学的终极目标,是让人类远离病痛,拥抱希望。”这一信念,将继续指引他在医学教育和科研的道路上砥砺前行。
人物简介:
陈建国,湖北赤壁人,1963年4月出生,现任华中科技大学同济医学院药理学系二级教授,博士生导师,华中学者讲席教授。1985年获咸宁医学院(现湖北科技学院)本科毕业,学士学位,1990年获同济医科大学(现华中科技大学)硕士学位,1995年赴德国凯泽斯劳藤大学作访问学者,1998年获德国海德堡大学博士学位。1998-2001年期间在美国爱荷华大学从事博士后研究。2002年作为“人才引进”回国,任国家重点(培育)学科《药理学》学科带头人、国家教学名师、国家精品课程《药理学》负责人,是长江学者特聘教授、国家杰出青年基金获得者,国家自然科学基金创新研究群体、教育部创新团队负责人。2015-2024年期间任华中科技大学党委常委、副校长、同济医学院党委书记、院长,兼任生物医药研究院常务副院长、国家重大新药创制科技专项首席科学家、国家中药药理三级实验室主任等职。曾任中国药理学会副理事长,现任神经精神药理专业委员会副主任委员。此外,还担任多个国内外学术期刊主编或编委,主编多部国家级规划教材。他主持多项国家级科研项目,包括科技部“脑科学与类脑研究”重大项目、国家973计划等,在Nature、Nature Metabolism、Cell Metabolism等国际著名期刊发表论文200余篇,其中SCI收录180余篇,他引8000余次。曾获国家教学成果奖二等奖、教育部自然科学奖一等奖、湖北省自然科学一等奖等多项荣誉,指导的博士生也多次获得优秀论文奖项。
2025-12-19
本期内容聚焦于2025年12月10日至12月17日的淋巴瘤研究动态,精心筛选并汇总了多项具有代表性的前沿研究进展。为了方便读者更好地把握研究方向,我们将这些文献进行分类整理,力求呈现一个系统、全面的研究概览。 本文汇总了滤泡性淋巴瘤及相关血液肿瘤领域的最新高影响力研究,涵盖药物开发、治疗策略、诊断技术及基础机制。
发表在《Lancet》的三期临床试验显示,艾波替单抗联合来那度胺和利妥昔单抗治疗复发或难治性滤泡性淋巴瘤患者,总缓解率和无进展生存期显著优于传统方案,且安全性可控,或将成为新的二线标准治疗。
《J Clin Oncol》报道,通过前瞻性队列验证,循环肿瘤DNA检测在大B细胞淋巴瘤一线治疗结束时可灵敏识别残留病变,预后评估优于传统PET-CT,为精准疗效监测提供新工具。
《Cancer Discovery》分析了2001年至2022年美国儿童及青少年癌症发病率趋势,揭示不同癌种发病率的复杂变化,提示环境和技术因素共同影响,为未来癌症防控策略提供数据支撑。
《NPJ Biofilms Microbiomes》综述了利用CRISPR技术工程肠道微生物组作为活体治疗剂的新兴策略,展示其在调节免疫、靶向血液肿瘤方面的巨大潜力及临床转化前景,代表肿瘤免疫治疗的新方向。
《J Clin Oncol》还报道了活检前使用类固醇不会降低弥漫性大B细胞淋巴瘤的诊断成功率,支持临床合理使用类固醇缓解症状而无须担心影响诊断准确性。
整体研究为滤泡性淋巴瘤及相关血液肿瘤的个性化治疗和精准管理提供了重要理论基础和临床指导。
药物类:
1.Lancet(IF:88.5):Epcoritamab、来那度胺和利妥昔单抗联合治疗复发或难治性滤泡性淋巴瘤对比来那度胺和利妥昔单抗的疗效(EPCORE FL-1):一项全球、开放标签、随机、Ⅲ期临床试验;
2.Lancet Haematol(IF:17.7):Epcoritamab单药治疗Richter转化(EPCORE CLL-1):一项单臂、多中心、开放标签、Ib/II期临床试验结果;
3.Blood Adv(IF:7.1):维奈托克拉与伊布替尼联合可在边缘区淋巴瘤中诱导持久的临床反应;
治疗类
1.Lancet(IF:88.5):复发或难治性滤泡性淋巴瘤治疗的进展;
2.J Clin Oncol(IF:41.9):弥漫大B细胞淋巴瘤中嵌合抗原受体T细胞治疗:长期获益与现实世界的复杂性;
3.Hemasphere(IF:14.6):原发性纵隔B细胞淋巴瘤CAR-T细胞治疗失败后的结局与治疗模式:DESCAR-T分析;
4.Mol Ther(IF:12.0):FcεRγI通过Syk-NFκB轴促进犬CD8嵌合抗原受体T细胞的细胞毒性;
5.Br J Dermatol(IF:9.6):BI17 全身性硬皮病伴发间变性淋巴瘤和霍奇金淋巴瘤:两例报告;
6.Br J Dermatol(IF:9.6):PA40 儿童B细胞淋巴母细胞淋巴瘤;
7.Br J Dermatol(IF:9.6):P025 原发性皮肤外结外型鼻型NK/T细胞淋巴瘤:病例报告;
8.Br J Dermatol(IF:9.6):P159 Besremi®(聚乙二醇化干扰素-α2b)在皮肤T细胞淋巴瘤治疗中的应用;
9.Br J Dermatol(IF:9.6):O11 斑片状预后:早期菌落型真菌病进展相关预后因素及一线治疗选择的识别;
10.Br J Dermatol(IF:9.6):BI10 (P084) 临床试验向实践转化:单中心29例菌落型真菌病和Sézary综合征患者使用mogamulizumab的真实世界经验;
11.Br J Dermatol(IF:9.6):P084 临床试验向实践转化:单中心29例菌落型真菌病和Sézary综合征患者使用mogamulizumab的真实世界经验;
12.Br J Dermatol(IF:9.6):P085 国际银屑病理事会成员对伴发肿瘤患者的银屑病处方实践调查;
13.Br J Dermatol(IF:9.6):PD12 窄谱紫外B和补骨脂素加紫外A光疗治疗菌落型真菌病:一所大学教学医院17年回顾性队列研究(2007-2024);
14.Br J Dermatol(IF:9.6):BI07 (P086) 伴发肿瘤重症银屑病患者的管理:一项回顾性观察研究;
15.Br J Dermatol(IF:9.6):P086 伴发肿瘤重症银屑病患者的管理:一项回顾性观察研究;
16.Br J Dermatol(IF:9.6):PA26 青少年患者毛囊型菌落型真菌病伴大细胞转化;
17.NPJ Biofilms Microbiomes(IF:9.2):CRISPR工程化微生物组:活体治疗革新血液肿瘤免疫治疗;
18.Haematologica(IF:7.9):利妥昔单抗、地塞米松、依托泊苷、异环磷酰胺和卡铂(R-DeVIC)在复发或难治性中枢神经系统淋巴瘤中的应用——一项回顾性多中心临床研究;
19.J Transl Med(IF:7.5):纳米医学在淋巴瘤治疗中的协同创新:系统综述;
20.J Transl Med(IF:7.5):褐藻多糖通过激活STAT3通路增强CAR-T细胞对非霍奇金淋巴瘤的抗肿瘤效应;
手术类:
近期在该领域未有新的文章,敬请期待
诊断类:
1.J Clin Oncol(IF:41.9):大B细胞淋巴瘤一线治疗后循环肿瘤DNA可测残留病变的前瞻性验证;
2.JAMA Netw Open(IF:9.7):活检前使用类固醇与弥漫大B细胞淋巴瘤患者诊断阳性率的关系;
3.Br J Dermatol(IF:9.6):DP06 组织学解码:γδ T细胞淋巴瘤与肿瘤期蕈样肉芽肿的鉴别;
4.Br J Dermatol(IF:9.6):DP08 2岁儿童发病的淋巴细胞样丘疹病(LyP):探讨儿童LyP诊断难点的病例报告;
其他类:
1.Cancer Discov(IF:33.3):2001年至2022年美国儿童及青少年癌症发病率趋势;
2.Br J Dermatol(IF:9.6):P087 并非蕈样肉芽肿;
3.BMC Med(IF:8.3):酒精摄入与癌症风险:四个生物库与联盟数据的孟德尔随机化分析;
药物类:
1. Epcoritamab、来那度胺和利妥昔单抗联合治疗复发或难治性滤泡性淋巴瘤对比来那度胺和利妥昔单抗的疗效(EPCORE FL-1):一项全球、开放标签、随机、Ⅲ期临床试验
期刊名称:Lancet
影响因子:88.5
JCR分区:Q1
作者:Lorenzo Falchi(一作),Franck Morschhauser(通讯)
单位:Universite de Lille, Centre Hospitalier Universitaire de Lille, Groupe de Recherche sur les Formes Injectables et les Technologies Associees (ULR 7365-GRITA), Lille, France
DOI:https://doi.org/10.1016/S0140-6736(25)02360-8
摘要:
【背景】复发或难治性滤泡性淋巴瘤患者迫切需要无化疗的方案以诱导持久缓解。Lenalidomide加rituximab(R2)是该人群的标准治疗。EPCORE FL-1试验评估了加入epcoritamab的R2方案对比单独R2的疗效和安全性。
【方法】该多国开放标签三期临床试验中,患者随机分配至固定疗程的epcoritamab联合R2组或R2组。主要终点为独立评审委员会评定的总缓解率和无进展生存期。
【结果】共488名患者随机分配,epcoritamab联合R2组总缓解率为95%,明显高于R2组的79%(p<0.0001);无进展生存期显著延长(16个月估计无进展生存率85.75%对40.72%,p<0.0001)。3级及以上不良事件在联合组更常见(90%对68%),但均可管理,细胞因子释放综合征主要为轻度。
【结论】epcoritamab联合R2显示出更高的治疗反应和更长的无进展生存期,安全性可控,提示其可作为滤泡性淋巴瘤二线及以后治疗的新标准。
【资助】AbbVie和Genmab。
总结:本全球三期随机试验显示,在复发或难治性滤泡性淋巴瘤患者中,epcoritamab联合lenalidomide和rituximab(R2)相比单纯R2治疗,显著提高了总缓解率和无进展生存期,且安全性在可控范围内,主要为轻度细胞因子释放综合征。该方案有望成为该患者群体的新的标准二线及后续治疗选择。
2. Epcoritamab单药治疗Richter转化(EPCORE CLL-1):一项单臂、多中心、开放标签、1b/2期临床试验结果
期刊名称:Lancet Haematol
影响因子:17.7
JCR分区:Q1
作者:Arnon P Kater(一作),Rebecca Valentin(通讯)
单位:Genmab, Copenhagen, Denmark
DOI:https://doi.org/10.1016/S2352-3026(25)00327-8
摘要:
【背景】Richter转化是治疗难度较大的B细胞淋巴瘤,尤其是合并高风险慢性淋巴细胞白血病特征或既往接受过治疗者。中位生存期仅6-12个月。本研究评估了皮下注射CD3×CD20双特异性抗体epcoritamab单药治疗Richter转化患者的安全性及初步疗效。
【方法】该多国、多中心、开放标签1b/2期试验在24个中心进行,纳入年龄≥18岁且经组织学确认的Richter转化(弥漫大B细胞淋巴瘤)患者,最多接受过两线治疗。epcoritamab采用逐步加量后维持48mg给药,主要终点为Lugano 2014标准下的总体反应率。
【结果】共纳入42例,随访中位22.9个月,总体反应率为47.6%(95% CI 32.0-63.6),未达到预设50%假设。首次治疗组反应率57.1%,二线及以上组38.1%,TP53异常患者40%。常见3-4级不良事件包括中性粒细胞减少、贫血和血小板减少。细胞因子释放综合征发生率86%,大多为1-2级。无治疗相关死亡。
【结论】epcoritamab单药在Richter转化中显示出有意义的抗肿瘤活性和可控的安全性,支持其作为治疗选项的进一步研究。
总结:这项涵盖42例Richter转化患者的多中心1b/2期临床试验显示,epcoritamab单药具有良好的抗肿瘤效果,尤其对首次治疗患者效果更佳。虽然总体反应率未达到50%的预设标准,但安全性良好,细胞因子释放综合征多数为轻中度,未见治疗相关死亡,提示该药物可能成为Richter转化新的治疗选择,值得进一步验证和推广。
3. 伊布替尼联合维奈托克在边缘区淋巴瘤中诱导持久临床反应
期刊名称:Blood Advances
影响因子:7.1
JCR分区:Q1
作者:Sasanka M Handunnetti(一作),Constantine S Tam(通讯)
单位:Alfred Hospital and Monash University, East Melbourne, Australia
DOI:https://doi.org/10.1182/bloodadvances.2025016646
摘要:口服伊布替尼(I)和维奈托克(V)作为单药治疗边缘区淋巴瘤(MZL)显示一定疗效,但完全缓解率较低。伊布替尼联合维奈托克(I+V)在其他恶性肿瘤中表现出较好的临床活性和可接受的耐受性。本研究为单中心2期临床试验,采用每日伊布替尼560mg起始,4周后维奈托克逐周递增至每日400mg,联合用药直至疾病进展或耐受性不佳。主要终点为第16周完全缓解率(CR)。通过骨髓和外周血流式细胞术评估微小残留病(MRD),MRD清除者可选择中断治疗。15例患者接受治疗,14例纳入疗效分析,15例纳入安全性分析。总体缓解率为79%,第16周CR率为29%,56周最佳CR率为57%,显著高于历史伊布替尼单药3%的CR率(p < 0.001)。56周MRD清除率为40%。6例MRD阴性完全缓解患者选择中断治疗,其中4例中位随访4年仍无疾病复发。整体中位随访5.5年,5年无进展生存率估计为56%。I+V安全有效,且完全缓解率显著优于伊布替尼单药,MRD阴性患者表现出持久缓解。
总结:本研究显示伊布替尼联合维奈托克在边缘区淋巴瘤患者中显著提高了完全缓解率,且治疗安全可耐受。联合用药不仅提升了疗效,还实现了部分患者的微小残留病清除,允许在治疗中断后长期维持无疾病状态,提示该组合方案为边缘区淋巴瘤的有效治疗选择,具有较好的临床应用前景。
治疗类
1. 复发或难治性滤泡性淋巴瘤治疗的一大进步
期刊名称:Lancet
影响因子:88.5
JCR分区:Q1
作者:Laura Magnano(一作),Laura Magnano(通讯)
单位:Haematology Department, Hospital Clinic of Barcelona, IDIBAPS, Barcelona 08036, Spain
DOI:https://doi.org/10.1016/S0140-6736(25)02436-5
摘要:本文综述了复发或难治性滤泡性淋巴瘤(FL)治疗领域的新进展,重点介绍了最新疗法如何改善患者预后及治疗选择。随着分子靶向药物和免疫疗法的引入,患者的治疗应答率及生存期显著提升。文章评估了多种新兴治疗策略的疗效与安全性,强调精准医学在FL管理中的重要性,为临床提供了更具针对性和个体化的治疗方案。
总结:该文章全面回顾了复发或难治性滤泡性淋巴瘤的治疗进展,特别是新型靶向疗法和免疫治疗的应用,显著推动了治疗效果的提升。创新点在于结合了最新临床试验数据,展示了个体化治疗策略的潜力,进一步丰富了FL的治疗选项,为临床医生在面对复发或难治病例时提供了更有力的依据和希望,代表了该领域治疗的一大步前进。
2. 弥漫性大B细胞淋巴瘤中嵌合抗原受体T细胞治疗的桥梁:长期获益与现实世界复杂性
期刊名称:J Clin Oncol
影响因子:41.9
JCR分区:Q1
作者:Priyanka A Pophali(一作),Christi Ann Hayes(通讯)
单位:Darthmouth-Hitchcock Medical Center, Lebanon, NH
DOI:https://doi.org/10.1200/JCO-25-02323
摘要:嵌合抗原受体(CAR)T细胞疗法已成为弥漫性大B细胞淋巴瘤(DLBCL)治疗的重要突破,显示出显著的长期生存获益。然而,现实世界中该疗法的应用面临多重挑战,包括患者选择、治疗相关毒性管理及疗效持续性的复杂性。文章综述了CAR T细胞疗法在DLBCL中的最新进展,强调了临床试验与实际临床应用之间的差距,并探讨了如何优化治疗策略以提升患者预后。
总结:本文全面解析了CAR T细胞疗法在弥漫性大B细胞淋巴瘤中的长期疗效及其现实临床应用中的复杂因素,创新性地桥接了临床试验数据与真实世界经验,揭示了疗法推广中的关键障碍和管理策略,为未来个体化治疗方案设计和优化提供了重要参考,推动该领域向更精准和安全的方向发展。
3. 原发性纵隔大B细胞淋巴瘤CAR-T细胞治疗失败患者的治疗结局与模式:DESCAR-T分析
期刊名称:Hemasphere
影响因子:14.6
JCR分区:Q1
作者:Jean Galtier(一作),Vincent Camus(通讯)
单位:Centre Henri Becquerel Departement d'Hematologie Rouen France
DOI:https://doi.org/10.1002/hem3.70263
摘要:本研究分析了原发性纵隔大B细胞淋巴瘤(PMBCL)患者在接受CAR-T细胞治疗失败后的治疗结局和治疗模式。通过DESCAR-T数据库收集数据,评估该患者群体的生存率和后续治疗反应。研究揭示CAR-T治疗失败后患者的总体预后较差,且后续治疗选择多样,包括化疗、放疗及其他免疫治疗。研究强调了对该高风险患者群体优化治疗策略的必要性。
总结:该研究系统评估了原发性纵隔大B细胞淋巴瘤患者在CAR-T细胞治疗失败后的临床结局,为后续治疗策略提供了重要参考。创新点在于利用DESCAR-T数据库的真实世界数据,全面揭示了这一特殊群体的治疗模式和生存状况,强调了进一步探索有效治疗方案的急迫性,推动了对CAR-T失败患者管理的深入理解。
4. FcεRγI促进犬CD8嵌合抗原受体T细胞通过Syk-NFκB轴的细胞毒性作用
期刊名称:Mol Ther
影响因子:12.0
JCR分区:Q1
作者:Emma E Goodman(一作),Aimee S Payne(通讯)
单位:Department of Dermatology, Columbia University, New York, NY 10032
DOI:https://doi.org/10.1016/j.ymthe.2025.12.010
摘要:比较肿瘤学促进了癌症免疫疗法的发展,然而犬类嵌合抗原受体T细胞(CART)治疗的细胞机制尚未被充分理解。在首次犬类临床试验中,携带犬源4-1BB-CD3ζ(cBBζ)结构域的抗CD20 CART诱导了CD20阴性淋巴瘤的生长,但未能持续存在或耗竭B细胞。本文显示,采用人源4-1BB-CD3ζ(hBBζ)的犬CART表现出更优越的治疗功能,这种增强作用通过FcεRγI介导。hBBζ-CART在重复杀伤实验和犬B细胞白血病异种移植模型中表现出更强的细胞溶解作用和CD8 T细胞增殖。转录组分析揭示CD8 hBBζ-CART中FCER1G及类先天免疫基因的上调。CRISPR介导的FCER1G敲除及药理学抑制Syk/NFκB通路的实验表明,Syk-NFκB信号调控FcεRγI介导的hBBζ-CART细胞毒性增强,伴随颗粒酶B及IFNγ/TNFα的增加。Syk-NFκB信号促进hBBζ CART中FcεRγI的表达,且CAR-TCR相互作用可增强NFκB信号,进一步上调FcεRγI并提升CART功能。该研究鉴定了一种由hBBζ信号诱导的功能强大的类先天免疫犬CART亚群,具有改善犬类及人类CART治疗的潜力。
总结:本研究创新地揭示了人源4-1BB-CD3ζ信号域通过FcεRγI和下游Syk-NFκB通路促进犬CD8 CART细胞增强细胞毒性和功能的机制。相比犬源信号结构域,hBBζ改善了CART的持续性和杀伤能力,为犬类肿瘤免疫治疗提供了新策略,并为人类CART疗法的优化提供了重要的机制依据和潜在靶点。研究强调了CAR-TCR相互作用在增强NFκB信号及FcεRγI表达中的关键作用,推动了嵌合抗原受体工程设计的新方向。
5. 广泛硬皮病伴间变性淋巴瘤及霍奇金淋巴瘤:两例病例报告
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Saerrah Murryam(一作),Janakan Natkunarajah(通讯)
单位:未提供
DOI:https://doi.org/10.1093/bjd/ljaf085.426
摘要:
在淋巴瘤背景下管理广泛硬皮病存在显著挑战,因需平衡免疫抑制治疗与肿瘤治疗的复杂性,且自身免疫病患者接受免疫抑制时淋巴瘤转化或复发风险增加。文中报道了两例案例:第一例为59岁女性,既往患有结节性淋巴细胞优势型霍奇金淋巴瘤(NLPHL),治疗后缓解,后出现广泛皮肤硬化和活动性红斑,接受甲氨蝶呤、脉冲甲泼尼龙、羟氯喹及UVA1光疗,后淋巴瘤复发并转化为T细胞丰富型B细胞淋巴瘤,经过化疗后缓解,硬皮病复发并继续接受治疗且反应良好;第二例为54岁女性,既往有银屑病和干燥综合征,出现广泛硬皮病后用羟氯喹和甲氨蝶呤治疗,4个月内发现颈部淋巴结肿大,确诊为IVB期间变性大细胞淋巴瘤,停用免疫抑制药,初始化疗效果差,计划进行替代化疗及自体干细胞移植。这些病例强调了广泛硬皮病与淋巴瘤之间的复杂关系,需个体化治疗方案,权衡免疫抑制与肿瘤治疗,且多学科协作至关重要。
总结:
该文报道了广泛硬皮病合并淋巴瘤的两例罕见病例,揭示了免疫抑制治疗与恶性肿瘤管理之间的复杂平衡。创新点在于详细描述了硬皮病的治疗过程中淋巴瘤的发生及转化,强调了自身免疫病患者中免疫抑制可能诱发或加重恶性淋巴瘤的风险。作者提出应根据患者具体情况调整治疗策略,结合多学科团队协作,实现免疫调节与肿瘤治疗的优化,从而改善患者预后。此研究为临床治疗广泛硬皮病合并恶性淋巴瘤提供了宝贵的经验和指导。
6. 儿科患者的B细胞淋巴母细胞淋巴瘤
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Evangelia Vetsiou(一作),Emilia Duarte(通讯)
单位:未知
DOI:https://doi.org/10.1093/bjd/ljaf085.399
摘要:一名5个月大的女婴因头皮出现两个逐渐增大的肿块就诊,最初被误诊为鳞屑斑块并使用局部抗真菌药物治疗。随后转诊至皮肤科,发现皮下有一个坚实2×2厘米的结节,超声显示皮下积液,活检取材为柔软有弹性的物质。组织学诊断为B细胞淋巴母细胞淋巴瘤(B-LL),免疫组化对CD79a、PAX5和CD19呈阳性。骨髓活检显示微量浸润(0.04%),脑脊液无肿瘤细胞。患者转至专科儿科血液肿瘤中心,开始UKALL方案治疗,初期对化疗反应良好。B-LL为罕见儿科疾病,多见于6岁以下儿童,男性略多。其特征为淋巴母细胞主要浸润淋巴结,较少累及骨髓,与急性淋巴细胞白血病不同。病因不明,可能与基因突变(如GATA3、CEBPE、ARID5B、IKZF1、CDKN2A)及环境因素(如电离辐射)有关,尤其是唐氏综合征儿童。B-LL常无症状,表现为皮肤、软组织或淋巴结肿块,诊断早期困难,治疗延迟。预后受年龄、临床表现及遗传异常影响,携带KMT2A易位的婴儿预后较差。及时诊断及应用UKALL方案治疗对改善患儿预后至关重要。
总结:该病例报告强调了B细胞淋巴母细胞淋巴瘤在婴幼儿中罕见且易误诊的特点,揭示其临床表现多样且早期无明显症状,提示需高度警惕皮下结节的恶性可能。文中结合免疫组化及骨髓检测,明确诊断并应用标准化UKALL化疗方案,显示出良好初期疗效。此外,综述了B-LL的遗传及环境相关因素,及其与急性淋巴细胞白血病的区别,为临床诊断和治疗提供了重要参考。创新点在于详细报道罕见病例的诊断过程及疗效,强调早期识别和规范治疗的重要性,助力提升儿科血液肿瘤的诊治水平。
7. P025 原发性皮肤外周型自然杀伤/T细胞淋巴瘤,鼻型:一例报告
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Awadh Alamri(一作),Atheer Aljehani(通讯)
单位:
DOI:https://doi.org/10.1093/bjd/ljaf085.053
摘要:
原发性皮肤外周型自然杀伤/T细胞淋巴瘤,鼻型(ENKTCL)是一种罕见且侵袭性强的皮肤T细胞淋巴瘤亚型,常与EB病毒(EBV)相关,表现为溃疡性皮肤病变,易误诊为感染或炎症性疾病。本文报道一例63岁慢性乙型肝炎患者,出现腹部及左大腿疼痛性硬化坏死性溃疡,初被误诊为脓疱疮,经抗生素治疗和清创后,病理检查显示EBV阳性淋巴细胞伴血管侵犯,确诊为ENKTCL。免疫组化显示CD20异常表达,颗粒酶B及EBV编码RNA阳性,CD3及CD56阴性。采用吉西他滨与奥沙利铂化疗后病情明显改善,辅以放疗治疗难治病灶,但疾病仍进展,需继续联合放化疗。ENKTCL多见于40-58岁男性,常累及鼻腔及皮肤、胃肠道等鼻外部位,表现为无痛结节进展为坏死性溃疡。诊断依赖组织病理及免疫组化,EBV检测为关键。CD20异常表达增加诊断难度,PAX-5阴性有助鉴别。治疗依据分期,早期以放疗为主,晚期联合放化疗,联合治疗优于单一疗法。该病例强调早期识别和准确诊断的重要性,提示需对该疾病保持高度警惕,并加强随访和治疗策略优化。
总结:
本病例报告详述了一例罕见的原发性皮肤外周型自然杀伤/T细胞淋巴瘤(鼻型)的诊断与治疗过程,突出EBV阳性淋巴细胞及免疫组化异常表达特点,特别是CD20的异常表达对诊断的挑战。文章创新点在于结合临床、病理及免疫组化结果,强调了早期鉴别诊断的重要性,以及联合放化疗在疾病管理中的优势。该报告提醒临床医生对类似溃疡性皮肤病变应高度警惕可能的ENKTCL,及时进行EBV检测和组织活检,以避免误诊,促进早期干预,从而改善预后。此外,提示该病易复发,需持续随访和个体化治疗策略。
8. Besremi®(聚乙二醇化干扰素α-2b)在皮肤T细胞淋巴瘤治疗中的应用
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Mary Wain(一作),Stephen Morris(通讯)
单位:University Hospitals Birmingham NHS Foundation Trust
DOI:https://doi.org/10.1093/bjd/ljaf085.187
摘要:自1980年代以来,干扰素α被用于治疗菌状息肉病(MF)和Sézary综合征(SS)。1型干扰素(IFN-α和IFN-β)具有抗病毒、抗肿瘤、免疫调节和抗增殖功能。最初上市的IFN-α-2b(Intron®)获批用于皮肤T细胞淋巴瘤,但因供应商财务问题被撤市,患者转用IFN-α-2a(Roferon®),Roferon后亦被撤市,患者转用聚乙二醇化IFN-α-2a(Pegasys®)。2023年欧洲肿瘤研究与治疗组织指南推荐使用Pegasys,因其每周一次给药且疗效相当。当前因制造问题,Pegasys国际短缺,医院采取减频给药和暂停新患者治疗等措施。英国现有的唯一可用IFN-α产品为Ropeginterferon-α-2b(Besremi®),原用于骨髓增殖性肿瘤,可每两周皮下注射一次。研究中21名Pegasys患者减频至隔周给药,9人皮肤恶化,6人转用Besremi,初步观察显示Besremi疗效至少相当于Pegasys,部分患者皮肤和心情改善。1例患者首次用药后出现严重不良反应,但后续耐受良好。本文报道了Besremi在MF/SS中的剂量调整、疗效、安全及监测的初步结果。
总结:本研究创新性地应对Pegasys短缺问题,首次系统评估了Besremi作为替代干扰素α制剂治疗皮肤T细胞淋巴瘤的应用。Besremi具有类似药代动力学且给药间隔更长的优势,初步疗效与安全性令人鼓舞,表明其可作为Pegasys的有效替代选项,为临床治疗提供了新的策略和依据。未来需进一步大规模研究验证其长期疗效与安全性。
9. 早期期髓样真菌病中与进展相关的预后因素识别及一线治疗选择
期刊名称:British Journal of Dermatology
影响因子:9.6
JCR分区:Q1
作者:Abraham Bashir(一作),Julia Scarisbrick(通讯)
单位:University of Southampton, UK
DOI:https://doi.org/10.1093/bjd/ljaf085.026
摘要:
晚期髓样真菌病(MF)和Sèzary综合征预后较差,生存期通常小于5年,且超过25%的早期MF患者会进展为晚期疾病。欧洲肿瘤研究与治疗组织推荐早期MF对皮肤定向治疗无反应者采用系统免疫治疗,但各中心治疗选择差异较大。PROCLIPI研究于2015年启动,涵盖52个国际中心,共纳入2172例MF/Sèzary患者,其中74.7%为早期疾病(IA-IIA)。影响疾病进展的因素包括皮肤斑块、淋巴结受累、年龄>60岁及皮肤大细胞转化。五年总生存率依分期显著不同(IA 94.3%、IB 84.3%、IIA 74.3%)。对397例早期MF患者一线治疗分析显示,治疗异质性大,84%为皮肤定向治疗,11%为系统治疗,7%为观察管理。皮肤定向治疗的总体应答率为73.9%,系统治疗为59%。FMF患者和IIA期患者的一线治疗响应率较低,分别为45%和57%的无应答率。研究显示早期MF虽被视为低级别淋巴瘤,但其生存率及预后存在显著差异,提示需早期识别高危患者,优化治疗策略以改善预后。
总结:
本研究创新性地通过国际多中心前瞻性队列(PROCLIPI)系统评估早期髓样真菌病患者的预后因素和治疗效果,明确了皮肤斑块、淋巴结受累、年龄和大细胞转化等为疾病进展的重要指标。研究揭示早期MF患者生存率明显低于传统认知,尤其是IB和IIA期患者,提示早期MF并非均质的低风险疾病。同时,治疗选择差异大且某些亚组(FMF及IIA期)对现有一线治疗响应较差,强调了建立个体化预后模型和精准治疗方案的迫切需求。这为临床识别高危患者及制定更有效的治疗策略提供了重要依据。
10. BI10 (P084) 将临床试验转化为实践:单中心29例患者使用mogamulizumab治疗菌状息肉病和塞扎里综合征的真实世界经验
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:James Ellis(一作),通讯作者未标明
单位:未知
DOI:https://doi.org/10.1093/bjd/ljaf085.419
摘要:Mogamulizumab在治疗塞扎里综合征(SS)和菌状息肉病(MF)恶性细胞中显示出疗效。本回顾性真实世界评估研究描述了英国一家三级皮肤T细胞淋巴瘤中心中mogamulizumab的治疗结果。共分析29例患者(SS 20例,MF 9例),起始治疗平均年龄66岁,所有患者均曾接受过系统治疗。主要终点为持续≥4个月的客观缓解率(ORR4),次要终点包括客观缓解率(ORR)、无进展生存期(PFS)、缓解时间及下次治疗时间。结果显示ORR4为27.6%,ORR为39.3%,SS患者CR为21%,MF患者无CR。中位PFS为9个月,血液缓解率高达92.3%。不良反应以轻度皮疹(36%)和输注反应(14%)为主,2例因不良反应停止用药。研究确认了mogamulizumab在真实世界中的疗效,与临床试验数据相符。
总结:本研究首次系统回顾了英国单中心使用mogamulizumab治疗SS和MF的真实世界数据,验证了其临床试验中的疗效与安全性。创新点在于详尽分析了血液和皮肤病变的不同缓解率,并报道了治疗持续时间及不良反应管理,提供了宝贵的临床实践参考,助力优化该药物在皮肤T细胞淋巴瘤中的应用。
11. P084 将临床试验转化为实践:单中心29例患者中使用mogamulizumab治疗菌状息肉病和Sèzary综合征的真实世界经验
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:James Ellis(一作),Sean Whittaker(通讯)
单位:未知
DOI:https://doi.org/10.1093/bjd/ljaf085.112
摘要:Mogamulizumab已被证实能有效针对Sèzary综合征(SS)和菌状息肉病(MF)中的恶性细胞。本回顾性真实世界评估研究描述了英国三级皮肤T细胞淋巴瘤中心使用mogamulizumab的治疗结果。研究纳入29名患者(20例SS,9例MF),平均起始治疗年龄66岁,所有患者均曾接受过系统治疗。患者大多处于晚期血液受累阶段,治疗中位时间7个月。主要疗效指标为持续≥4个月的客观缓解率(ORR4)为27.6%,总体客观缓解率为39.3%,完全缓解率为14.3%。SS患者缓解率优于MF,血液缓解率达92.3%。中位无进展生存期为9个月,副作用以轻度皮疹和输注反应为主,部分严重不良反应导致停药。该研究确认了mogamulizumab在真实临床环境中的有效性,疗效和安全性与临床试验数据相符,提供了宝贵的实践数据支持其在SS和MF治疗中的应用。
总结:本研究真实反映了mogamulizumab在临床实践中对SS和MF患者的疗效及安全性,特别是对血液受累患者展现出较高的缓解率。研究创新性地将临床试验结果转化为真实世界数据,验证了该药物在多系统受累晚期患者中的应用效果和耐受性,为临床医生提供了重要的治疗参考依据。
12. 同时患有恶性肿瘤的银屑病患者用药实践调查:国际银屑病理事会成员的问卷研究
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Stephanie Bowe(一作),Michelle Murphy(通讯)
单位:未知
DOI:https://doi.org/10.1093/bjd/ljaf085.113
摘要:
伴有恶性肿瘤的中重度银屑病患者治疗面临独特挑战。生物制剂虽革新了银屑病治疗,但因恶性肿瘤患者被排除在临床试验之外,系统性和生物制剂在该人群中的安全性和疗效数据稀缺。临床医生多依赖注册数据、真实世界证据及专家意见。此研究通过向141名国际银屑病理事会成员发放电子问卷,调查其对伴有恶性肿瘤患者中重度银屑病系统和生物治疗的处方习惯,涵盖五种恶性肿瘤类型及不同缓解期。57名专家回应,结果显示抗IL-17制剂在缓解期患者中最常用,反映出对其安全性的信心提升;而在活动期恶性肿瘤患者中,阿普斯特(apremilast)被优先选择,特别是乳腺癌、黑色素瘤及转移性肾癌患者。TNF-α抑制剂和富马酸酯类药物使用最少。多数专家认为现有指南在恶性肿瘤背景下治疗银屑病缺乏明确性,近半数总是咨询肿瘤科团队,强调多学科协作的重要性。该研究揭示处方实践差异显著,显示对抗IL-17制剂及阿普斯特的偏好,呼吁制定基于长期安全数据的恶性肿瘤专属治疗指南,以优化决策和患者结局。
总结:
本研究首次系统调查国际银屑病专家在伴恶性肿瘤患者中使用系统性和生物制剂的临床决策,突显了当前治疗实践的多样性和指南不足的问题。创新点在于明确了专家对不同恶性肿瘤状态下药物选择的偏好,尤其是抗IL-17制剂和阿普斯特的广泛接受,及强调了多学科合作的重要性。这为未来制定更具针对性的临床指南和安全性研究提供了宝贵依据,推动该复杂患者群体的规范化管理。
13. 窄波紫外线B和补骨脂素加紫外线A光疗治疗菌状息肉病:一项为期17年的回顾性队列研究(2007-2024)
期刊名称:British Journal of Dermatology
影响因子:9.6
JCR分区:Q1
作者:Thandiwe Banda(一作),Amirtha Rajasekaran(通讯)
单位:University Teaching Hospital
DOI:https://doi.org/10.1093/bjd/ljaf085.264
摘要:菌状息肉病(MF)是最常见的皮肤T细胞淋巴瘤亚型,英国年发病率为每10万人0.7例。由于其慢性且常进展性特点,治疗目标为控制症状、延缓病程及改善生活质量。窄波紫外线B(NB-UVB)和补骨脂素加紫外线A(PUVA)是早期MF管理中的常用光疗方法。本研究回顾分析了2007年至2024年间大学教学医院接受NB-UVB或PUVA治疗的32例经活检确诊的早期MF患者(IA-IIB期)。结果显示,44%患者完全缓解,47%部分缓解,9%无反应。年轻年龄和较高累计光疗剂量与更好预后相关,但统计学无显著性(P=0.93和P=0.08);男性疗效较女性好,但亦无显著差异(P=0.71)。34%患者复发,25%维持缓解。完全缓解中位治疗次数为30次,NB-UVB与PUVA间缓解率无显著差异。光疗耐受良好,仅3例出现轻微不良反应。研究证实NB-UVB及PUVA对早期MF均有效,提示未来需更大规模及更长随访研究以优化治疗方案。
总结:该研究系统评估了NB-UVB和PUVA光疗在早期菌状息肉病中的长期临床效果,揭示约半数患者可达完全缓解,且大多数患者有一定程度的治疗反应。尽管年龄、性别和累计剂量与疗效呈相关趋势,但未达统计学显著,提示个体化治疗仍需探索。研究创新点在于提供了大型单中心17年治疗数据,比较了两种光疗方式的效果与安全性,为早期MF光疗选择提供了重要临床依据。未来研究应聚焦于优化光疗剂量及识别影响疗效的关键患者特征。
14. 严重银屑病合并恶性肿瘤患者的管理:一项回顾性观察研究
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Puo Nen Lim(一作),Gabrielle Becher(通讯)
单位:Tertiary Dermatology Centre
DOI:https://doi.org/10.1093/bjd/ljaf085.416
摘要:生物制剂治疗已彻底改变了银屑病的管理,在临床试验和真实世界研究中显示出良好的疗效和安全性。尽管生物制剂尚未被证实增加恶性肿瘤风险,但针对近期诊断恶性肿瘤患者的相关数据有限。本研究为一项在三级皮肤科中心进行的回顾性观察,涵盖2019年11月至2024年12月期间49例严重银屑病合并恶性肿瘤患者,平均年龄62岁。收集患者基本信息、银屑病分型、PASI和DLQI评分、癌症类型及治疗情况。患者中女性占多数,银屑病以斑块型为主。癌症类型主要为乳腺癌、非霍奇金淋巴瘤、结肠癌及直肠癌。癌症诊断时,多数患者停用生物制剂,部分患者继续使用。恶性肿瘤治疗期间银屑病表现稳定,但治疗后常有加重。癌症治疗后,41%患者重新开始生物制剂治疗。研究发现生物制剂在控制严重银屑病的同时并未显著影响癌症治疗效果,且安全性良好。多学科合作和个体化治疗决策对患者管理至关重要。
总结:本研究创新地系统回顾了严重银屑病患者合并恶性肿瘤时的治疗管理,强调生物制剂在此类复杂患者中的安全性和有效性。研究支持在多学科团队指导下,针对患者具体癌症类型和银屑病情况,合理调整生物制剂使用,有助于同步控制银屑病和恶性肿瘤,避免治疗冲突,提高患者生活质量。此项研究为临床实践提供了重要循证依据,填补了恶性肿瘤患者使用生物制剂治疗银屑病的知识空白。
15. 严重银屑病合并恶性肿瘤患者的管理:一项回顾性观察研究
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Puo Nen Lim(一作),Areti Makrygeorgou(通讯)
单位:Tertiary Dermatology Centre
DOI:https://doi.org/10.1093/bjd/ljaf085.114
摘要:生物制剂治疗革新了银屑病的管理,临床试验和现实研究均证实其疗效与安全性。尽管生物制剂未显示增加恶性肿瘤风险,但针对近期恶性肿瘤患者的使用数据有限。本研究回顾性分析了2019年11月至2024年12月间在三级皮肤科中心49例严重银屑病合并恶性肿瘤患者的管理情况。患者平均年龄62岁,女性占多数,最常见的银屑病类型为斑块型,癌症以乳腺癌、非霍奇金淋巴瘤、结肠癌和直肠癌为主。癌症诊断时多数患者停止生物制剂治疗,少数患者持续使用。银屑病在化疗期间通常稳定,治疗后常出现复发。恶性肿瘤治疗后,41%的患者恢复使用生物制剂。癌症进展导致18%患者死亡,10%患者在使用生物制剂过程中出现复发或新发恶性肿瘤。研究强调个体化治疗、跨学科合作和共享决策的重要性,表明生物制剂在恶性肿瘤患者中控制严重银屑病既有效又较为安全。
总结:本研究创新在于系统回顾严重银屑病合并恶性肿瘤患者的生物制剂管理实践,证实了生物制剂在癌症患者中可安全有效地控制银屑病,且在癌症治疗期间多采取暂停策略,治疗后适时恢复,降低风险同时保证疾病控制。该研究强调多学科协作与个体化治疗,填补了生物制剂在合并恶性肿瘤患者中的使用数据缺口,为临床决策提供了重要依据。
16. 青少年患者的滤泡向性真菌样肉芽肿伴大细胞转化
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Natalie King Stokes(一作),Julia Scarisbrick(通讯)
单位:University of Manchester
DOI:https://doi.org/10.1093/bjd/ljaf085.385
摘要:一名19岁男性因头部、颈部及四肢出现持续3年的硬化斑块伴毛囊突出被转诊至皮肤淋巴瘤门诊,初诊为湿疹。皮肤活检确诊为滤泡向性真菌样肉芽肿(FMF),病理显示显著的毛囊周围淋巴细胞浸润及CD7缺失,CD4:CD8比例>20:1。初步分期为IIa期,行窄波紫外线B照射后虽有良好反应但两月内复发。后续淋巴结活检及皮肤活检发现大细胞转化及CD30表达,确诊为IVa2期FMF伴淋巴结受累。患者先后接受甲氨蝶呤和布伦妥昔单抗治疗,后计划行造血干细胞移植。儿童青少年MF罕见且诊断延迟常超过3年,滤泡向性亚型具有侵袭性且少见大细胞转化。该病例强调了滤泡向性真菌样肉芽肿在年轻患者中可能的严重临床进展及治疗挑战,且当前缺乏系统管理指南,国际共识建议建立登记系统以优化治疗策略。
总结:本研究报告了青少年滤泡向性真菌样肉芽肿(FMF)伴大细胞转化的罕见病例,揭示此疾病在年轻患者中虽少见但具有侵袭性进展和复杂治疗需求。该病例首先通过临床和病理诊断明确,随后经历了治疗反应和复发,最终确认大细胞转化和淋巴结受累,提示疾病进展至晚期。治疗上,患者对传统甲氨蝶呤无效,改用靶向药物布伦妥昔单抗获得部分缓解并计划进行造血干细胞移植。文章创新点在于聚焦于儿童及青少年FMF的临床表现、诊断延迟及治疗难题,强调了建立国际注册和共识的重要性,以应对该罕见但预后不良的疾病亚型。此病例为临床医生提供了宝贵的诊疗经验,有助于未来优化针对性治疗方案的制定。
17. CRISPR工程微生物组:活体治疗革新血液癌症免疫治疗
期刊名称:NPJ Biofilms Microbiomes
影响因子:9.2
JCR分区:Q1
作者:Fang Cheng(一作),Fang Cheng(通讯)
单位:河南省郑州市河南中医药大学第三附属医院
DOI:https://doi.org/10.1038/s41522-025-00882-9
摘要:血液癌症如白血病、淋巴瘤和多发性骨髓瘤因免疫逃逸、抗原异质性及治疗相关毒性,许多患者治疗难以奏效。本文综述了利用CRISPR工程改造的肠道共生菌作为精准“活体治疗剂”,以调节宿主免疫和直接靶向恶性克隆的新策略。文章围绕三大主题展开:(1)CRISPR工程共生菌调节免疫及抗癌机制;(2)实现活体治疗的技术及递送平台,包括CRISPR变体、噬菌体/脂质纳米颗粒递送、基因电路及生物安全控制;(3)转化进展、技术与安全挑战及伦理监管考量。通过工程菌分泌免疫调节因子、靶向递送肿瘤溶解载荷和产生抗癌代谢物三种具体治疗模式,利用现代CRISPR与合成生物学工具包实现。部分动物模型显示显著抗肿瘤效果(肿瘤缩小超过60%),并在控制环境中恢复CAR-T细胞功能,但疗效在不同模型间差异较大,人类临床转化尚未证实。文章还分析了菌株稳定性、生物安全性及脱靶效应等技术瓶颈,提出利用营养依赖型杀灭开关和人工智能优化菌株等方案,并展望了体内噬菌体递送、多组学驱动患者分层等未来方向。CRISPR微生物组编辑代表血液肿瘤学的范式转变,提供局部、持续且系统毒性低的新型治疗手段。
总结:该综述创新性地提出利用CRISPR技术改造肠道共生菌作为“活体治疗剂”,以精准调控宿主免疫系统和直接作用于血液癌细胞,克服传统免疫治疗中抗原异质性和免疫逃逸的难题。通过合成生物学和先进递送技术实现菌株的安全控制和功能定制,展现了显著的抗肿瘤潜力。文章不仅总结了当前的技术进展和临床前成果,还深入分析了关键技术和安全挑战,提出了创新性解决方案,强调了伦理和监管方面的考虑。未来方向包括基于多组学的患者精准分层和体内递送系统的优化,预示CRISPR微生物治疗在血液肿瘤免疫领域的广阔应用前景。
18. 复发或难治性中枢神经系统淋巴瘤中利妥昔单抗、地塞米松、依托泊苷、异环磷酰胺和卡铂联合方案(R-DeVIC)回顾性多中心临床研究
期刊名称:Haematologica
影响因子:7.9
JCR分区:Q1
作者:Kudret Kama(一作),Kudret Kama(通讯)
单位:Department of Hematology, Oncology, Stem-Cell Transplantation and Palliative Care, Klinikum Stuttgart, Stuttgart
DOI:https://doi.org/10.3324/haematol.2025.287982
摘要:暂无摘要内容。
总结:本研究为一项回顾性多中心临床研究,聚焦于复发或难治性中枢神经系统淋巴瘤患者,评估R-DeVIC方案(利妥昔单抗、地塞米松、依托泊苷、异环磷酰胺和卡铂联合用药)的疗效和安全性。尽管摘要未提供具体数据,但该研究的创新点在于系统性地回顾并分析了该联合化疗方案在临床中的应用情况,为未来设计更有效治疗策略提供了临床实践依据,特别是在难治性神经系统淋巴瘤治疗领域中填补了疗效证据的空白。研究强调了多中心合作的重要性,有助于提高样本量和结果的普遍性。
19. 淋巴瘤治疗中纳米医学的协同创新:系统评价
期刊名称:J Transl Med
影响因子:7.5
JCR分区:Q1
作者:Yingying Zhang(一作),Zihang Chen(通讯)
单位:四川大学华西医院病理科
DOI:https://doi.org/10.1186/s12967-025-07249-w
摘要:
纳米医学在淋巴瘤治疗中的应用近年来取得了显著进展,本文系统回顾了纳米技术在淋巴瘤药物递送、诊断和治疗策略中的创新和协同效应。纳米载体通过提高药物的靶向性和生物利用度,显著改善了治疗效果并减少了副作用。同时,多功能纳米平台实现了诊疗一体化,增强了早期检测和个性化治疗的能力。本文还探讨了纳米医学结合免疫疗法和基因治疗的潜力,展望了未来临床转化的挑战和机遇。总体而言,纳米医学的协同创新为淋巴瘤患者提供了更精准和有效的治疗方案,推动了淋巴瘤治疗领域的突破与发展。
总结:
该系统评价全面梳理了纳米医学在淋巴瘤治疗中的多方面创新,尤其强调了纳米载体在药物递送和诊断中的协同作用,提升了治疗的精准度和安全性。文章创新性地整合了纳米技术与免疫疗法、基因治疗的结合,展示了未来多学科交叉融合的趋势和潜力。此外,作者对纳米医学临床应用中存在的障碍进行了深入分析,提出了促进技术转化的策略,具有重要的指导意义和实践价值。此文为淋巴瘤精准治疗提供了新的思路和理论支持,推动了纳米医学在肿瘤治疗领域的进一步发展。
20. 复合多糖褐藻糖胶通过激活STAT3通路增强抗CD19 CAR-T细胞治疗非霍奇金淋巴瘤的抗肿瘤效果
期刊名称:Journal of Translational Medicine
影响因子:7.5
JCR分区:Q1
作者:Qingzheng Kang(一作),Xuanren Shi(通讯)
单位:深圳大学总医院血液与肿瘤科
DOI:https://doi.org/10.1186/s12967-025-07548-2
摘要:
【背景】尽管嵌合抗原受体T细胞(CAR-T)疗法取得进展,但仍面临T细胞耗竭加剧和体内持久性差的难题。当前通过共表达细胞因子提升CAR-T功能的策略往往引发严重副作用,尤其是细胞因子释放综合征。因此,亟需开发更安全且可持续的营养干预手段以改善CAR-T的抗肿瘤疗效。褐藻糖胶(FO)是一种来源于海洋植物的生物活性多糖,已显示免疫调节和与传统化疗的协同潜力,但其在细胞免疫疗法中的作用尚未探明。本研究旨在阐明FO在非霍奇金淋巴瘤CAR-T治疗中的功能,并为其临床转化提供理论依据。
【方法】通过体外和体内实验研究FO对抗CD19 CAR-T细胞的影响,利用流式细胞术分析CAR-T细胞的记忆和耗竭表型,检测不同处理组CAR-T的细胞毒性和细胞因子释放,并在肿瘤移植小鼠模型中评估FO对CAR-T功能的辅助作用,同时通过抑制剂验证其激活的信号通路。
【结果】FO显著增强CAR-T细胞的记忆保持与耐耗竭能力,提高其抗氧化能力、增殖水平并减少活化细胞凋亡,从而提升并维持了CAR-T细胞在体外及异种移植模型中的抗肿瘤活性。机制研究显示FO通过激活STAT3信号通路,作为CAR-T细胞功能的增强剂发挥作用。
【结论】本研究揭示了FO作为免疫调节补充剂在增强CAR-T细胞抗肿瘤功能中的支持作用,显示其在非霍奇金淋巴瘤CAR-T治疗中的临床应用潜力。
总结:本研究创新性地发现海洋多糖褐藻糖胶能够通过激活STAT3信号通路,有效增强抗CD19 CAR-T细胞的记忆维持、抗耗竭能力和抗氧化水平,显著提升其体内外抗肿瘤效果。相比传统通过细胞因子共表达提升CAR-T功能但带来严重副作用的方法,FO作为一种营养干预策略,展现出更安全且可持续的潜力,为细胞免疫治疗尤其是非霍奇金淋巴瘤的CAR-T疗法提供了新的辅助治疗手段和临床转化路径。
手术类:
近期在该领域未有新的文章,敬请期待
诊断类:
1. 一线治疗后大B细胞淋巴瘤患者循环肿瘤DNA可测量残留病变的前瞻性验证
期刊名称:J Clin Oncol
影响因子:41.9
JCR分区:Q1
作者:Steven Wang(一作),Steven Wang(通讯)
单位:Department of Hematology, Amsterdam UMC-Location Vrije Universiteit, Cancer Center Amsterdam, Amsterdam, The Netherlands
DOI:https://doi.org/10.1200/JCO-25-01712
摘要:
[目的] 由于正电子发射断层扫描(PET)阳性预测值有限,治疗结束(EOT)时大B细胞淋巴瘤(LBCL)患者的疗效评估仍不理想。基于循环肿瘤DNA(ctDNA)的可测量残留病变(MRD)检测提供了一种微创手段,可能改善预后评估。我们前瞻性评估了采用PhasED-Seq技术在一线LBCL患者治疗结束时的MRD检测。
[方法] 患者纳入HOVON-902前瞻性队列,接受根治性一线治疗。通过肿瘤活检或治疗前血浆识别并追踪相位变异(PV)。比较EOT ctDNA-MRD状态与国际预后指数(IPI)及EOT PET-CT对无进展生存期(PFS)和总生存期(OS)的预后价值。
[结果] 136例中134例(99%)成功识别PV。EOT时83%患者MRD阴性,17%阳性。MRD阳性与预后不良显著相关:3年PFS阳性组17%,阴性组85%(HR 9.8,P=9.63×10^-12);OS分别为43%与92%(HR 7.7,P=1.27×10^-6)。多因素分析显示MRD为独立预后因素。MRD阳性的阳性预测值优于PET(68% vs 56%,P≤.001),阴性预测值相似。MRD阳性患者在完全代谢缓解和非完全代谢缓解亚组中均有较高复发风险。
[结论] 本研究验证了PhasED-Seq技术在一线治疗LBCL患者中超灵敏ctDNA-MRD检测的临床价值,支持将MRD纳入临床疗效评估体系。
总结:该研究通过前瞻性队列验证了利用PhasED-Seq技术检测大B细胞淋巴瘤患者一线治疗结束时循环肿瘤DNA中可测量残留病变的有效性。结果显示MRD阳性患者的复发率和死亡率显著高于MRD阴性者,且MRD检测的阳性预测值优于传统的PET-CT检查。MRD作为独立预后指标,能够更准确地辅助判断患者预后,提示其在临床疗效评估中的潜在应用价值。
2. 预活检类固醇与弥漫性大B细胞淋巴瘤患者的诊断成功率
期刊名称:JAMA Netw Open
影响因子:9.7
JCR分区:Q1
作者:Sathwik Madireddy(一作),Ari Pelcovits(通讯)
单位:Division of Hematology/Oncology, Brown University Health, Providence, Rhode Island
DOI:https://doi.org/10.1001/jamanetworkopen.2025.48617
摘要:
【重要性】类固醇常用于弥漫性大B细胞淋巴瘤(DLBCL)患者的症状管理,但临床上长期存在预活检使用类固醇可能降低诊断准确性的担忧。系统性DLBCL患者中类固醇与活检结果的关联尚未被研究。
【目的】评估预活检类固醇使用是否影响新诊断DLBCL患者的诊断成功率。
【设计、地点与参与者】回顾性病例系列,涵盖2015年至2024年间,布朗大学附属三级学术医疗系统新诊断DLBCL的成人患者,排除复发、难治性DLBCL及原发中枢神经系统淋巴瘤患者。采用逻辑回归分析类固醇暴露(剂量、持续时间及停药天数)与诊断成功率的关系。
【暴露】活检前30天内使用类固醇。
【主要结局】初次活检DLBCL诊断成功率、重复活检比例及首次阴性活检至化疗启动时间。
【结果】320例患者中,48人(15%)接受预活检类固醇。类固醇组诊断成功率为83%,非类固醇组为81%,差异无统计学意义(PR=1.03,95%CI 0.89-1.18)。阴性首次活检患者的治疗启动时间在两组间无显著差异。类固醇剂量、使用时长及停药天数与诊断成功率无显著关联。活检方式显著影响诊断成功率:核心针和细针穿刺活检分别比切除和切开活检的诊断成功率低12%和69%。
【结论与意义】在320例DLBCL患者中,预活检类固醇使用并未降低诊断成功率或延迟治疗启动,活检方式对诊断成功影响最大,支持在淋巴瘤评估过程中合理使用类固醇的临床策略。
总结:本研究回顾了320例新诊断弥漫性大B细胞淋巴瘤患者,发现活检前使用类固醇不会显著影响活检的诊断成功率,也不会延迟后续治疗的启动。诊断成功率与活检技术关系更大,切除或切开活检优于针吸活检。该结果为临床中合理使用类固醇以缓解症状提供了证据支持,无需担心影响诊断准确性。
3. γδ T细胞淋巴瘤与肿瘤期菌状息肉病的鉴别诊断
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Nishita Jain(一作),Ashima Lowe(通讯)
单位:未提供
DOI:https://doi.org/10.1093/bjd/ljaf085.329
摘要:我们报告一例78岁会计师患者,既往有直肠癌和膀胱癌病史,出现快速发展的广泛皮肤病变,表现为红至紫色斑块和结节,迅速增大至5-6厘米。抗生素治疗无效,超声检查提示皮肤厚度异常,皮肤活检显示表皮变薄,基底层空泡样变及大量小淋巴细胞和组织细胞浸润。免疫组化证实为T细胞表型,CD8+细胞缺失CD5和CD2但保留CD7,Ki-67约30%。考虑为皮肤γδ T细胞淋巴瘤(PCGDTCL)或CD8+菌状息肉病肿瘤期,克隆性研究提示为成熟激活γδ T细胞克隆性增殖。伴有JAK3和MAPK1突变及TCR-γ和TCR-δ重排,影像学无系统性累及。经全身电子束治疗后完全缓解。PCGDTCL极为罕见,临床表现进展快,病理特征与菌状息肉病肿瘤期重叠,诊断及治疗复杂,需多学科协作制定个体化方案。
总结:本文报道一例罕见的原发性皮肤γδ T细胞淋巴瘤,患者表现为快速进展的多发皮肤病变,病理和免疫表型复杂,需与肿瘤期菌状息肉病鉴别。结合分子遗传学检测确认诊断,患者对全身电子束治疗响应良好。该病例强调了罕见皮肤T细胞淋巴瘤诊断的挑战性和多学科合作的重要性,以指导个体化治疗。
4. 儿童期发病的淋巴样丘疹病(LyP)病例报告:探讨LyP在儿童中的诊断难点
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Taherah Khan(一作),Tanya Bleiker(通讯)
单位:未提供通讯作者单位信息
DOI:https://doi.org/10.1093/bjd/ljaf085.331
摘要:淋巴样丘疹病(LyP)是一种罕见的原发性皮肤CD30+ T细胞淋巴增生性疾病,表现为反复出现的红斑结节,常见于四肢。发病机制尚不明确,可能与病毒感染有关。LyP在儿童中极为罕见,诊断困难且易与其他良恶性疾病混淆。本文报道一例2岁男童从8个月大开始出现非瘙痒性丘疹,经皮肤活检确诊为LyP。该病分为五种亚型,但对预后和治疗无明显影响。治疗包括局部类固醇、光疗及系统性甲氨蝶呤。LyP虽多呈良性,但与血液恶性肿瘤相关,需长期随访和密切临床病理结合诊断。
总结:本病例详细描述了儿童期LyP的临床表现及诊断过程,强调其诊断的挑战性和需警惕与其他疾病的鉴别。LyP虽罕见且多呈良性,但因其与血液系统恶性肿瘤的关联,需进行长期监测和综合诊断判断。治疗选择多样,需根据病情综合评估。该病例强调了临床与病理的紧密结合对于LyP诊断的重要性。
其他类:
1. 2001年至2022年美国儿童及青少年癌症发病率趋势分析
期刊名称:Cancer Discovery
影响因子:33.3
JCR分区:Q1
作者:Meredith S Shiels(一作),Meredith S Shiels(通讯)
单位:National Cancer Institute, Rockville, MD, United States
DOI:https://doi.org/10.1158/2159-8290.CD-25-1493
摘要:我们利用美国癌症统计数据库的全国数据,估算了2001-2022年间0-19岁儿童及青少年癌症的年龄标准化发病率趋势。整体癌症发病率为每10万人中18.2例,2001-2016年间年增长0.94%,2016-2022年间年下降0.96%。淋巴瘤发病率在2001-2022年间每年增长0.49%。白血病发病率2001-2010年增长1.03%,随后趋于平稳。中枢神经系统肿瘤2001-2014年增长0.81%,2014-2022年下降2.10%。其他上皮性肿瘤2001-2013年稳定,2013-2016年上升,2016-2022年再次稳定。2022年新增约1040例儿童癌症诊断,相较于2001年的预期病例数。癌症分类、筛查及诊断技术的变化,连同潜在风险因素,可能共同影响了发病率的变动。
总结:该研究揭示了美国儿童及青少年癌症发病率在过去二十余年的变化趋势,显示整体发病率先升后降,不同癌种表现出不同的变化轨迹。技术进步和疾病分类调整对统计数据影响显著,同时提示环境和其他潜在风险因素的作用,强调需持续监测和深入研究癌症发病机制。
2. P087 不是单纯的真菌病——难治性皮肤T细胞淋巴瘤患者中的真菌感染案例分析
期刊名称:Br J Dermatol
影响因子:9.6
JCR分区:Q1
作者:Ji Fung Yong(一作),Kevin Molloy(通讯)
单位:未提供
DOI:https://doi.org/10.1093/bjd/ljaf085.115
摘要:皮肤T细胞淋巴瘤的常见类型为真菌病样肉芽肿(MF)和Sézary综合征(SS)。本文报道5例在MF/SS治疗过程中被诊断为“真性真菌病”的患者,真菌感染表现为环状鳞屑性皮疹,病原均为红色毛癣菌(Trichophyton rubrum)。患者均在抗真菌治疗后症状改善。MF/SS患者因表皮屏障受损和肿瘤微环境偏向Th2,易发生慢性皮肤真菌感染,且MF/SS的治疗(如局部皮质类固醇、光疗和系统疗法)会进一步抑制免疫功能,增加感染风险。研究强调在MF/SS患者中出现 atypical 新皮疹时,应考虑合并真菌感染的可能,避免误诊及延误治疗。
总结:这篇文章通过五个病例,说明MF/SS患者中真菌感染可能被误认为是疾病本身的进展,尤其在免疫抑制治疗期间。MF/SS患者因皮肤屏障和免疫状态异常,易发生真菌感染,且真菌感染临床表现与MF类似,易被忽视。及时进行皮肤活检和真菌培养对鉴别诊断和合理治疗至关重要。临床医生应警惕MF/SS患者新出现的非典型皮疹可能为继发感染,避免误诊导致治疗失败。
3. 酒精消费与癌症风险:四个生物库和联盟数据的孟德尔随机化分析
期刊名称:BMC Med
影响因子:8.3
JCR分区:Q1
作者:Susanna C Larsson(一作),Stephen Burgess(通讯)
单位:British Heart Foundation Cardiovascular Epidemiology Unit, Department of Public Health and Primary Care, University of Cambridge, Cambridge, UK
DOI:https://doi.org/10.1186/s12916-025-04543-8
摘要:[背景] 酒精消费与癌症风险相关,证据最强的七种癌症包括乳腺癌、结直肠癌、食管癌、肝癌、口腔癌、咽癌和喉癌。然而,孟德尔随机化支持因果效应的证据并不一致。[方法] 本研究进行全面孟德尔随机化分析,评估遗传预测的酒精消费与20种癌症风险的关联。使用95个与酒精消费相关的基因变异,主要分析包括欧洲血统的367,643名UK Biobank参与者、500,348名FinnGen参与者、169,312名All of US参与者和451,206名Million Veteran Program参与者,并在癌症特异性联盟中估计关联。[结果] 遗传预测酒精消费与总体癌症无显著关联(OR 0.96,p=0.45)。七种重点癌症中,头颈癌呈多重校正显著正相关(OR 1.51,p=0.001),结直肠癌(OR 1.21,p=0.035)和食管癌(OR 1.42,p=0.033)呈名义显著正相关。肝癌总体无显著关联,但Million Veteran Program和ADH1B-rs1229984变异显示名义显著正相关。乳腺癌无显著关联。肾癌(OR 0.64,p=0.0003)和子宫内膜癌(OR 0.56,p=0.0006)呈多重校正显著负相关,非霍奇金淋巴瘤、骨髓瘤及部分卵巢癌亚型呈名义显著负相关。癌症死亡率与酒精消费呈名义显著正相关,调整吸烟后减弱。研究限制包括基因工具的有效性、统计能力、检测率差异等。[结论] 研究支持酒精消费对头颈癌、食管癌和结直肠癌有一定因果影响,对肝癌证据不一致,对乳腺癌无证据,且表明酒精可能与某些癌症呈负相关。人类遗传数据未支持酒精消费导致所有癌症的观点。
总结:本研究利用孟德尔随机化方法分析遗传预测酒精消费与多种癌症风险的关系,发现酒精消费与头颈癌、食管癌及结直肠癌风险呈现一定正相关,但对肝癌和乳腺癌缺乏一致性证据。反而肾癌、子宫内膜癌及部分淋巴瘤和卵巢癌亚型显示负相关。总体来看,遗传数据不支持酒精是所有癌症的因果因素,提示酒精与某些癌症风险的关系更为复杂。
编辑:Dakota Z.
免责声明
本文旨在为医疗卫生专业人士传递更多医学资讯前沿,不能以任何方式取代专业的医疗指导,也不应被视为诊疗建议,本平台不推荐任何未获批的药品/适应证使用。部分内容由AI辅助生成,请注意甄别。
本内容系编译、摘录自公开出版或发表的学术研究论文。我们的目的是推动前沿临床知识的传播与普及,助力临床医疗质量发展。原始论文的全部著作权归原作者及/或出版方所有,本内容仅为学术报道与信息分享。如文章作者或版权持有者不希望被报道,请联系本媒体编辑(留言/添加微信 Jackzhao361),我们将立即处理并删除相关内容。感谢您的理解与支持!
免疫疗法临床3期临床结果
2025-12-07
前言 (Preface)
想象力的工业化:当软件渴望理解生命
在工业软件的三大巨头中,达索系统(Dassault Systèmes)无疑是最具哲学家气质的异类。如果说 Ansys 致力于求解物理方程的精度,Synopsys 致力于编织硅基芯片的密度,那么达索系统则致力于构建一个“和谐的宇宙”。
从 1981 年为了设计“幻影”战机而诞生的 CATIA 代码开始,这家法国公司就不仅仅满足于制造工具。在过去的 45 年里,它完成了一场惊心动魄的蜕变:从一家辅助绘图的软件商,进化为一家管理产品全生命周期(PLM)的平台商,最终在 2025 年成为了一家试图解码人体奥秘的生命科学巨头。
本研究通过五张高维度的全景表格,试图穿透“3D体验(3DEXPERIENCE)”那令人眼花缭乱的营销术语,直抵达索系统的商业核心:
1. 产品图谱:看它如何用“罗盘”将 12 个品牌统摄于四大象限,覆盖从矿山开采到药物研发的每一环。
2. 技术溯源:揭示 MatrixOne 的数据库技术如何成为平台的脊梁,以及 Medidata 如何注入了生物学的基因。
3. 创始人追踪:观察“法国皇室”般的稳定权力结构,与被收购的“硅谷游侠”们如何博弈。
4. 资本演进:复盘其家族控股背景下,以 10 年为周期的长视主义并购逻辑。
5. 战略归因:剖析其“消灭文件”、“定义概念”与“万物孪生”的底层哲学。
我们试图回答一个核心命题:一家欧洲家族企业,是如何在强敌环伺的科技丛林中,通过“重新定义工业语言”,一步步将原本冰冷的工业软件,变成了连接产品、自然与生命的通用语言?
如果说 Ansys 是“物理世界的求解者”,Synopsys 是“数字芯片的编织者”,那么 Dassault Systèmes (达索系统) 则有着更大的野心——它试图成为**“全宇宙的虚拟孪生(Virtual Twin Experiences of the Universe)”**。
达索系统的产品架构与前两家截然不同。它不再仅仅是一堆工具的集合,而是被强行统一在一个极其庞大的操作系统——3DEXPERIENCE Platform 之下。其产品线按照著名的“罗盘(The Compass)”逻辑分为四大象限。
以下是基于 2025年12月 视角的 Dassault Systèmes 产品图谱(Product Atlas)。Dassault Systèmes 产品图谱 (2025 终极版)
核心架构: 所有产品均通过 3DEXPERIENCE 平台 进行数据互通,分为四大象限:3D 建模、仿真与制造、社交与协作、信息智能。1. 西象限:3D 建模应用 (3D Modeling Apps)
塑造虚拟世界的形状与材料
品牌 (Brand)
核心产品/模块 (Key Products)
核心能力 (Core Capability)
典型应用/行业备注CATIACATIA 3DEXPERIENCE
高端 CAD/系统工程皇冠上的明珠
。航空航天(波音/空客)与汽车(宝马/特斯拉)的绝对标准。不仅是画图,更是基于模型的系统工程 (MBSE)。
CATIA Magic
(No Magic)
系统建模 (SysML)
复杂的系统架构设计,源自收购 No Magic。
ICEM Surf
A级曲面设计
汽车外形设计的顶级曲面工具。SOLIDWORKSSOLIDWORKS Desktop
主流 CAD
全球用户量最大的机械设计软件,主要面向中端市场及供应链。
3DEXPERIENCE Works
云端 CAD
SOLIDWORKS 的云原生版本,打通设计与制造。GEOVIASurpac
矿山规划
地质建模与采矿工程。
Minex
沉积层建模
煤矿及其他层状矿床的勘探与规划。
Whittle
露天矿优化
战略性矿山规划与经济分析。BIOVIADiscovery Studio
生命科学建模
分子建模、蛋白质模拟,用于药物发现。
Materials Studio
材料科学
电池材料、合金、聚合物的原子级模拟。
Pipeline Pilot
科学信息学
实验室数据管理与科学工作流自动化。2. 南象限:仿真与虚拟现实 (Simulation & V+R)
验证虚拟世界的功能与生产
品牌 (Brand)
核心产品/模块 (Key Products)
核心能力 (Core Capability)
典型应用/行业备注SIMULIAAbaqus
非线性有限元 (FEA)
结构仿真的黄金标准,特别擅长处理橡胶、碰撞等高度非线性问题。
CST Studio Suite
电磁仿真
源自收购 CST。5G、天线、电磁兼容性 (EMC) 分析。
PowerFLOW
空气动力学 (CFD)
源自收购 Exa。基于格子玻尔兹曼方法 (LBM) 的高精度流体,汽车风阻模拟标准。
XFlow
粒子流体 (CFD)
擅长自由液面(如涉水、齿轮箱润滑)模拟。
Simpack
多体动力学
机械系统(如列车、风机)的运动学分析。
fe-safe
疲劳分析
结构寿命预测。DELMIADELMIA Digital Mfg
数字化制造
虚拟工厂仿真、人体工程学、机器人路径规划。
DELMIA Quintiq
供应链优化
复杂的物流、排程与计划优化(SCP)。
DELMIA Apriso
制造运营管理 (MOM)
工厂车间执行系统 (MES) 与运营管控。3DEXCITEDELTAGEN
高端可视化
将 CAD 数据转化为照片级逼真的营销素材(VR/AR)。3. 东象限:信息智能应用 (Information Intelligence)
连接数据与临床试验
品牌 (Brand)
核心产品/模块 (Key Products)
核心能力 (Core Capability)
典型应用/行业备注MEDIDATARave EDC
电子数据采集生命科学板块的核心
。全球大多数临床试验数据的管理平台。
Medidata AI
临床数据分析
利用历史临床试验数据优化新药研发流程。
Patient Cloud
远程医疗
以患者为中心的移动端数据采集。NETVIBESExalead
企业搜索与索引
对企业海量数据进行索引和语义搜索。
Sourcing & Standardization
零部件标准化
AI 驱动的供应链零部件去重与标准化管理。4. 北象限:社交与协作 (Social & Collaborative)
管理全生命周期的数据
品牌 (Brand)
核心产品/模块 (Key Products)
核心能力 (Core Capability)
典型应用/行业备注ENOVIAPLM Backbone
也就是 ENOVIA企业的脊椎
。负责 BOM 管理、变更管理、配置管理。
3DEXPERIENCE Platform
基础架构
实际上是 ENOVIA 在底层支撑整个平台的单一数据源 (Single Source of Truth)。CENTRIC PLMCentric PLM
消费品 PLM独立运营
。专门针对时尚、零售、快消品的 PLM,市场占有率极高。3DSwymCommunities
社交协作
类似于企业内部的微信/Slack,但与 3D 模型深度集成。关键洞察 (Key Insights for 2025)
1. "从机械到生命" (From Things to Life):观察图谱你会发现,MEDIDATA (生命科学) 和 BIOVIA (材料/生物) 的权重在 2025 年极高。达索系统不再只是一家“造飞机汽车”的公司,它现在是全球最大的临床试验数据公司之一。这是它与 Ansys/Synopsys 最大的区别。
2. "以平台消灭工具" (Platform vs. Tools):Ansys 和 Synopsys 倾向于通过接口连接不同的工具(Connect),而达索系统的逻辑是**“消灭文件”。在 CATIA 和 SIMULIA 之间,理论上不需要转换文件格式,它们都在操作数据库中的同一个对象。这种以数据为中心 (Data-Centric)** 的架构是其 3DEXPERIENCE 平台的核心护城河。
3. "Centric 的特权":在所有品牌中,只有 CENTRIC PLM 保持了相对独立的“外挂”状态。这是因为快消行业的节奏与重工业完全不同,强行并入 3DEXPERIENCE 可能会“水土不服”。
4. "仿真全家桶":虽然 SIMULIA 的名气不如 Ansys 响亮,但通过收购 CST (电磁) 和 Exa (流体),SIMULIA 实际上已经构建了仅次于 Ansys 的多物理场能力,且在非线性结构 (Abaqus) 领域拥有绝对统治力。
这是达索系统 2025 年的产品全貌。接下来,我们可以进入 技术溯源维度,去看看这些庞大的品牌最初是从哪里来的。达索系统的技术溯源维度分析。
与 Synopsys 这种“硅谷猎手”式的技术拼图不同,达索系统的技术溯源呈现出一种“皇室联姻与领土扩张”的特征。它的起源是高贵的(航空航天),随后的每一步大动作(如收购 SolidWorks, MatrixOne, Medidata)都是为了建立一个新的“诸侯国”(Brand),并最终统一在 3DEXPERIENCE 的王旗之下。
表格说明:
1. 时间基准:2025年12月。
2. 品牌架构:达索系统以 12个品牌 (Brands) 管理产品,表格将按品牌归类。
3. 货币单位:由于达索是法国公司,部分早期收购以欧元 (€) 结算,后期大额收购多以美元 ($) 结算,表格中会注明。Dassault Systèmes 全产品图谱:技术溯源与身世背景表 (2025版)
品牌 (Brand)
核心产品/技术
核心功能
原所属公司 / 技术来源
收购/发布时间
收购金额
历史背景与核心人物 (Founders & Origins)CATIACATIA V5/V6
高端 CADDassault Aviation
(Internal)
1981年 (分拆)
-皇室血统
。最初是达索航空为了设计 Mirage (幻影) 战斗机而开发的内部工具(因为当时的 CADAM 只能画 2D)。核心人物:Francis Bernard (达索系统首任 CEO),被称为“CATIA 之父”。
ICEM Surf
A级曲面ICEM Technologies
2007年
未披露
源自大众汽车 (Volkswagen) 内部开发的曲面工具,是汽车外形设计的绝对标准。
Magic (No Magic)
MBSE 系统建模No Magic
2017年
未披露
位于美国的 SysML 建模领导者,补全了 CATIA 在系统工程 (Cyber-systems) 的能力。SOLIDWORKSSOLIDWORKS
主流 3D CADSolidWorks Corp.
1997年
3.10 亿美元达索史上最成功的防御性收购
。Jon Hirschtick (MIT背景) 创立了 SolidWorks,试图用 Windows PC 颠覆高端 CAD。达索将其买下作为中端防线,保持独立运作多年。SIMULIAAbaqus
非线性 FEAHKS
(Hibbitt, Karlsson & Sorensen)
2005年
4.13 亿美元SIMULIA 的基石
。由三位布朗大学博士创立,解决了高度非线性(如橡胶、碰撞)的仿真难题。
CST Studio
电磁仿真CST
(Germany)
2016年
2.20 亿欧元
德国达姆施塔特工业大学背景。补全了 5G/电子仿真能力。
PowerFLOW
气动/流体Exa Corp.
2017年
4.00 亿美元
基于格子玻尔兹曼 (LBM) 方法的 CFD,无需画网格,是汽车风阻模拟的标准。
XFlow
粒子流体Next Limit Dynamics
2016年
未披露
西班牙公司,源自电影特效技术(RealFlow),擅长模拟飞溅的液体。
Simpack
多体动力学Simpack
(Germany)
2014年
未披露
源自德国宇航中心 (DLR),专门解决机械系统运动学问题。
fe-safe
疲劳分析Safe Technology
2013年
未披露
英国公司,专注于金属疲劳寿命预测。ENOVIAENOVIA (MatrixOne)
PLM 核心平台MatrixOne
2006年
4.08 亿美元平台的心脏
。现在的 3DEXPERIENCE 底层架构其实主要源自 MatrixOne 的技术,而非达索早期的 VPM。MatrixOne 使得管理海量异构数据成为可能。
SmarTeam
中端 PLMSmart Solutions
1999年
3500 万美元
以色列公司,主要配合 SolidWorks 销售。DELMIADELMIA (Robotics)
机器人仿真Deneb Robotics
1997年
1.05 亿美元DELMIA 的起源
。Deneb 是当时离线编程 (OLP) 和数字工厂仿真的领导者。
Quintiq
供应链规划Quintiq
(Netherlands)
2014年
2.50 亿欧元
解决极其复杂的运筹学问题(如航空公司排班、物流路径)。
Apriso
制造执行 (MES)Apriso
2013年
2.05 亿美元
让达索从“虚拟制造”真正落地到“车间执行”。BIOVIADiscovery Studio
生命科学/材料Accelrys
2014年
7.50 亿美元
Accelrys 自身就是一家整合了 MSI, Synopsys (Chemical) 等多家科学软件的公司。被收购后更名为 BIOVIA。MEDIDATARave EDC
临床数据采集Medidata Solutions
2019年58 亿美元达索史上最大单笔收购
。彻底改变了公司基因,使其成为生命科学巨头。创始人:Tarek Sherif & Glen de Vries (后曾乘坐蓝色起源火箭进入太空,不幸于2021年空难去世)。GEOVIASurpac / GEMS
采矿规划Gemcom Software
2012年
3.60 亿美元
加拿大公司,全球最大的采矿软件供应商。被收购后改名为 GEOVIA。3DEXCITEDELTAGEN
高端可视化RTT
(Realtime Tech)
2013年
~1.50 亿欧元
德国公司,专门为汽车行业提供照片级实时的 VR/AR 营销素材。CentricCentric PLM
时尚 PLMCentric Software
2018年
控股收购
硅谷公司,创始人 Chris Groves。它是唯一被允许保持高度独立运营(甚至保留原名)的品牌,因为其在快消/时尚界的统治力太强。关键技术溯源洞察 (Technical Genealogy Insights)1. "MatrixOne":被遗忘的幕后英雄
现在的用户打开 3DEXPERIENCE 平台,觉得界面很炫酷。但支撑这个平台数据流转的“脊梁”——也就是 ENOVIA 的核心,其实很大程度上源自 2006 年收购的 MatrixOne。
• 归因:达索早期的 PDM (VPM) 适合管理极其复杂的 CAD 文件(如飞机),但缺乏灵活性。MatrixOne 带来了基于 Web 的、灵活的业务对象模型,这成为了后来达索“消灭文件 (Zero File)”理念的技术基石。2. "SolidWorks":最成功的防御战
1997 年,以 Jon Hirschtick 为首的 MIT 团队用 SolidWorks 掀起了“基于 Windows 的 3D CAD”革命。
• 归因:达索当时面临一个选择:要么看着 SolidWorks 吃掉中低端市场,要么买下它。达索选择了买下(仅用 3.1 亿美元),并极其明智地允许其独立发展,不强制将其与 CATIA 融合。这创造了 CAD 历史上最大的现金牛(Cash Cow)。3. "Medidata":基因突变
2019 年豪掷 58 亿美元 收购 Medidata,是达索技术基因的一次剧烈突变。
• 归因:在此之前,达索处理的是“几何与物理”(金属、塑料)。Medidata 处理的是“统计与临床”(病人、药物)。这次收购让达索拥有了全球最大的临床试验数据库,使其能在 2020 年代提出“人体数字孪生 (Virtual Twin of the Human)”这一宏大愿景。4. "SIMULIA" 的拼图逻辑
与 Ansys 自研起家不同,SIMULIA 完全是“买出来”的:
• 结构靠 Abaqus (HKS)。
• 流体靠 Exa (LBM方法) 和 XFlow (粒子法)。达索很有趣,它几乎放弃了传统的 Navier-Stokes 网格流体(如 Fluent),而是押注了下一代的无网格技术(LBM/Particle),这非常符合其追求“设计仿真一体化”的口味,因为无网格技术对几何清理的要求更低。
这份表格揭示了达索系统如何从一家飞机设计软件商,通过“选准赛道 -> 吞并龙头 -> 品牌化封装”的路径,变成了今天的全宇宙虚拟孪生帝国。达索系统的创始人追踪维度分析。
与 Synopsys 创始人多为“硅谷风投客”不同,达索系统的核心权力结构呈现出极其稳定的“法国皇室风格”—权力交接非常有秩序(从 Bernard 到 Edelstenne 到 Charlès 再到 Daloz),且核心高管任期极长。
但对于被收购的品牌(尤其是美国公司),达索系统表现出一种“总督制”:它倾向于让被收购公司的创始人留任一段时间(作为封疆大吏),但最终这些具有硅谷基因的创业者大多会选择离开,去寻找下一个从 0 到 1 的机会。
特别说明 (2025年12月视角):
1. 权力交接:2024-2025年是达索系统历史上最重要的权力交接期。长期掌舵的 Bernard Charlès 退居二线,Pascal Daloz 正式接棒 CEO。
2. 最新变动:Centric Software 的传奇创始人 Chris Groves 刚刚于 2025 年 10 月卸任 CEO,退居顾问。Dassault Systèmes 全产品图谱:创始人追踪与去向表 (2025版)
品牌/产品
原所属公司
核心创始人 & 行业地位
创始人现状 (截至 2025.12)Dassault Systèmes
(集团本身)Dassault Aviation
分拆:1981年Francis Bernard
地位:
CATIA 之父。他在幻影战机的设计部门领导开发了 CATIA。工程软件界的活化石。Charles Edelstenne地位: 商业大脑。达索家族的财务总管,一手建立了达索系统的商业帝国。Francis Bernard
:已退休多年,安享晚年。Charles Edelstenne:仍担任 荣誉主席 (Honorary Chairman),是董事会的精神领袖。Group Leadership
(核心高管)-Bernard Charlès
地位:
执掌公司 30 年的灵魂人物。定义了“PLM”和“3DEXPERIENCE”两个时代。工程界的乔布斯式人物。执行董事长
。2024年1月,他将 CEO 职位交给 Pascal Daloz,自己专注于长期战略与董事会事务。SOLIDWORKSSolidWorks Corp.
成立:1993年Jon Hirschtick
地位:
麻省理工 (MIT) 该领域的传奇。他用 $3.1亿 卖掉 SolidWorks 后,又创立了云 CAD Onshape (被 PTC 收购)。连环创业/竞争对手
。他离开达索后创立的 Onshape 现在是达索的竞争对手 (PTC) 的一部分。他目前是 PTC 的 EVP。MEDIDATAMedidata
成立:1999年Tarek Sherif
& Glen de Vries地位: 将临床试验带入云端。Glen de Vries 是一位极具冒险精神的科学家。Tarek Sherif
:2024-2025年逐渐淡出达索管理层,转型为投资人 (Ryght)。Glen de Vries:已故。2021年曾乘坐蓝色起源火箭进入太空,不幸于同年死于私人飞机事故。Exa (PowerFLOW)Exa Corp.
成立:1991年Stephen Remondi
地位:
致力于流体仿真方法的革新(LBM方法)。新创业
。收购一年后 (2018) 离开达索。现为生物科技公司 Xsphera Biosciences 的创始人兼 CEO。QuintiqQuintiq
成立:1997年Victor Allis
地位:
荷兰人工智能博士。将复杂的运筹学算法商业化用于排程。新创业
。收购完成后离开。现为美国 Activote (政治科技应用) 的联合创始人。CentricCentric Software
成立:2004年Chris Groves
地位:
时尚 PLM 领域的绝对霸主。他争取到了 Centric 在达索内部极高的独立性。刚刚卸任
。2025年10月,他正式辞去 CEO 职位,转任高级顾问。Fabrice Canonge 接任 CEO。CSTCST AG
成立:1992年Prof. Thomas Weiland
地位:
达姆施塔特工业大学教授。有限积分技术 (FIT) 的发明者。学术界/退休
。典型的德国学术派创始人,收购后回归学术与顾问角色,未进行再次创业。AbaqusHKS
成立:1978年Hibbitt, Karlsson & Sorensen
地位:
三位布朗大学博士。解决了非线性力学的计算难题。早已退休
。公司于 2005 年被收购,三位创始人在收购后不久即功成身退。深度画像:两种截然不同的“物种”
通过这张表格,我们可以清晰地看到达索系统生态中两种完全不同的“生物”:
1. 法国总部的“守护者” (The French Guardians)
• 代表人物:Bernard Charlès, Pascal Daloz, Charles Edelstenne。
• 特征:超长待机。他们不是连环创业者,而是职业生涯几乎全部奉献给一家公司的“教父”。
• 风格:擅长顶层设计、哲学思考(“Virtual Twin of the Universe”)和极其长期的战略规划。
• 现状:2025 年,随着 Pascal Daloz 接任 CEO,这个群体刚刚完成了一次平稳的代际更替。Daloz 曾是 Medidata 收购案的主导者,他的上台意味着“生命科学”战略将进一步强化。
2. 被收购的“美国/硅谷游侠” (The Silicon Valley Rangers)
• 代表人物:Jon Hirschtick (SolidWorks), Tarek Sherif (Medidata), Chris Groves (Centric), Stephen Remondi (Exa)。
• 特征:无法被驯服。他们拥有极强的个人魅力和创业精神。达索系统通常会给他们 1-5 年的“锁定期”或“自治期”(Centric 甚至保持了 7 年独立 CEO)。
• 结局:他们最终都会离开。因为达索系统的中央集权文化(The 3DEXPERIENCE Platform)要求所有品牌必须在底层打通,这往往与创始人追求独立灵活的理念冲突。Jon Hirschtick 创立 Onshape 就是为了“革自己的命”,这在达索体系内是不被允许的。
3. 2025 年的特殊节点:Centric 的 Chris Groves
• Chris Groves 是一个特例。他成功地让 Centric 在达索内部保持了极其罕见的独立性(甚至保留了硅谷总部和独立销售团队)。他直到 2025年10月 才卸任,这在达索的收购史上是非常长寿的创始人任期。这或许标志着达索终于要开始对 Centric 进行更深度的“平台化整合”了。
这张表格生动地展示了达索系统是如何通过“以法式中央集权吸纳美式创新技术”来构建帝国的。达索系统的资本演进维度分析。
与美国同行(Ansys/Synopsys)不同,达索系统作为法国CAC40指数成分股,其资本运作带有浓厚的“欧洲保守主义”与“家族长远眼光”相结合的色彩。
它很少进行频繁的小型并购,而是习惯长时间积累现金,然后每隔 7-10 年进行一次“赌上国运”级别的超大并购(SolidWorks -> MatrixOne -> Medidata),通过剧烈的无机增长(Inorganic)强行拓展疆土,随后进入漫长的消化期(Organic)。
特别说明 (2025年12月视角):
1. 货币单位:达索系统财报以 欧元 (€) 结算。历史并购金额保留原交易货币(通常为美元)。
2. 财年:与自然年一致(12月31日截止)。
3. 上市地点:Euronext Paris (巴黎泛欧交易所)。曾在纳斯达克上市,但于 2008 年自愿退市以降低合规成本,专注于巴黎主板。
4. 数据范围:涵盖 1996 年 IPO 至 2025 年。Dassault Systèmes 30年全景回顾:财务、并购与资本成长表 (1996-2025)
财年 (FY)
核心收购 / 重大事件
总营收 (Revenue €)
Y/Y 增长
增长构成分析 (Organic vs Inorganic)
当年市值范围 (Market Cap)
备注1996IPO (上市)
Paris & Nasdaq
€0.23 B
-Organic
作为达索航空的子公司上市,主要收入依赖 IBM 销售渠道。
€1.0 - €1.5 B
此时主要产品仅为 CATIA。1997SolidWorks
€0.30 B
+28%Inorganic 拐点
。$3.1亿收购 SolidWorks。营收开始多元化。
€1.5 - €2.2 B
确立了高端(CATIA)+中端(SW)的双轨战略。1998Matra Datavision
€0.42 B
+38%Inorganic
。收购 Matra 的部分产品,扩充 CAD 市场份额。
€2.0 - €3.5 B
互联网泡沫前夕,增长强劲。2000Delmia
(Deneb)
€0.63 B
+19%Inorganic
。整合 ENEA/Deneb 成立 DELMIA 品牌,进入数字制造。
€4.0 - €6.0 B
-2002
-
€0.77 B
+3%Organic 停滞
。航空业受到 911 事件影响,高端 CAD 需求放缓。
€3.5 - €4.5 B
-2005Abaqus
€0.93 B
+16%Inorganic 驱动
。$4.13亿收购 Abaqus,成立 SIMULIA 品牌。
€4.5 - €5.5 B
正式进入仿真市场。2006MatrixOne
€1.16 B
+24%Inorganic 爆发
。$4.08亿收购 MatrixOne。营收突破 10亿欧元大关。
€5.0 - €6.5 B
获得了构建 V6 平台的核心 PDM 技术。2008Nasdaq 退市
€1.34 B
+5%战略收缩
。自愿从纳斯达克退市,仅保留巴黎上市。
€3.5 - €5.0 B
金融危机期间,通过成本控制维持利润。2010Exalead
(搜索)
€1.56 B
+20%Organic 复苏
。经济复苏带动 SolidWorks 销量大增。
€6.0 - €8.0 B
提出 "3DEXPERIENCE" 愿景雏形。2012Gemcom
(GEOVIA)
€2.03 B
+14%Inorganic
。$3.6亿收购 Gemcom,进入采矿业。营收突破 20亿欧元。
€9.0 - €11 B
股价开始进入长牛周期。2014Accelrys / Quintiq
€2.29 B
+13%Inorganic 大年
。连续收购 Accelrys ($7.5亿) 和 Quintiq (€2.5亿),布局科学与规划。
€12 - €15 B
确立了“科学公司”的新定位。2016CST
(电磁)
€3.06 B
+8%Organic 为主
。CST 补充了 SIMULIA,但整体增长靠 3DEXPERIENCE 平台迁移驱动。
€17 - €20 B
-2017Exa Corp.
€3.23 B
+6%Mixed
。$4亿收购 Exa,补齐流体仿真。
€20 - €25 B
-2018Centric PLM
€3.48 B
+8%Inorganic
。收购 Centric 控股权,进入快消时尚领域。
€25 - €35 B
市场给予高估值。2019Medidata
(巨型收购)€4.02 B+16%历史性并购
。$58亿美元 收购 Medidata。这是达索赌上未来的一战。
€35 - €40 B
股价因收购带来的债务压力短期承压。2020
(COVID-19)
€4.45 B
+11%Inorganic 支撑
。Medidata 全年并表。临床试验业务因疫苗研发激增,抵消了工业软件的下滑。
€38 - €45 B
Medidata 证明了其抗周期能力。2021
-
€4.86 B
+9%Organic 反弹
。工业需求复苏 + 临床业务持续增长。€65 - €75 B历史市值高点
(科技股牛市)。2022Diota
(AR)
€5.67 B
+17%Organic 强劲
。汇率有利 (美元走强) + 订阅制转型加速。
€45 - €55 B
加息导致估值回调,但业绩依然稳健。2023
-
€5.95 B
+5%Organic
。生命科学业务遭遇周期性回调 (COVID后效应)。
€45 - €50 B
营收逼近 60亿欧元。2024CEO 交接
€6.45 B (预)
~+8%Mixed
。Pascal Daloz 接任 CEO。重点在于整合与利润率提升。
€40 - €48 B
市场等待生命科学业务的二次加速。2025AI / 医疗深化~€7.0 B
(预)~+9%Organic 为主
。利用 AI (Generative Experience) 提升 ARPU 值。€50 - €60 B
稳固欧洲最大软件公司之一的地位。资本演进四部曲 (Strategic Evolution Phases)
达索系统的资本故事可以清晰地划分为四个阶段,每个阶段都由一次**“核弹级”收购**开启:
1. 机械设计时代 (1996 - 2005)
• 核心事件:1997年收购 SolidWorks ($3.1亿)。
• 资本逻辑:利用 IPO 筹集的资金,买下最大的潜在对手。这次收购是完美的“现金奶牛”投资。SolidWorks 带来的充沛现金流,支持了达索后续 20 年的扩张。
• 营收规模:2亿 -> 9亿欧元。
2. 平台化时代 (2006 - 2013)
• 核心事件:2006年收购 MatrixOne ($4.08亿)。
• 资本逻辑:为了摆脱对“文件”的依赖,达索必须拥有一个数据库内核。MatrixOne 的收购虽然当时看很贵,但它成为了后来 ENOVIA V6 和 3DEXPERIENCE 的技术地基。没有它,达索依然只是一个工具软件商,成不了平台商。
• 营收规模:10亿 -> 20亿欧元。
3. 科学化时代 (2014 - 2018)
• 核心事件:2014年收购 Accelrys ($7.5亿)。
• 资本逻辑:达索判断物理世界(汽车/飞机)的增长将放缓,必须寻找新大陆。他们选择了“微观世界”(分子/材料)。这次收购标志着达索从“工程软件”向“科学软件”跨越。
• 营收规模:20亿 -> 35亿欧元。
4. 虚拟孪生与生命时代 (2019 - 2025)
• 核心事件:2019年收购 Medidata ($58亿)。
• 资本逻辑:这是达索历史上最大、最冒险的一次赌博。交易金额超过了达索当时市值的 1/5。
• Inorganic 爆发:这笔收购直接让生命科学板块的收入占比从 <5% 跃升至 ~20%。
• 抗周期性:2020年疫情期间,当波音和空客停止采购 CAD 软件时,Medidata 的临床试验业务支撑了整个集团的财报。
• 营收规模:40亿 -> 70亿欧元。025 年的资本画像 (The Financial Profile)
• 独特性:与 Synopsys/Ansys 相比,达索系统的家族控股特征明显。达索家族 (Groupe Industriel Marcel Dassault) 依然持有约 40% 的股份和 >50% 的投票权。这意味着管理层(Charles Edelstenne / Bernard Charlès)可以无视华尔街的季度盈利压力,进行以 10年 为周期的超长期战略布局。
• 估值逻辑:
• CATIA/SolidWorks 提供了类似债券的稳定现金流(Cash Cow)。
• Medidata/SIMULIA 提供了高增长的故事(Growth Engine)。
• 市场通常给予达索系统比传统工业软件更高的溢价,因为它是稀缺资产——欧洲唯一能与美国科技巨头抗衡的软件公司,且垄断了生命科学与高端制造的数据入口。
通过这张表,你可以看到达索系统不是在“经营”一家软件公司,而是在“统治”一个不断扩张的虚拟领土。每一次资本出手,都是为了吞并一个新的“省份”(从机械省,到流体省,再到生命省)。达索系统战略归因维度的深度分析。
如果说 Ansys 的战略是“深耕物理”,Synopsys 的战略是“融合硅与系统”,那么达索系统的战略则是最具哲学色彩和宏大叙事的。它不满足于制造软件工具,而是试图“重新定义工业的语言”。
达索系统的核心战略逻辑可以概括为:“用概念定义市场,用平台消灭文件,用孪生覆盖万物。”
以下是基于 2025 年视角,结合其历史演进的战略归因分析表。Dassault Systèmes 战略归因矩阵:定义权与控制权的进化史 (1981-2025)
战略阶段 (Strategic Phase)
核心战略口号 (Core Slogan)
关键动作 (Key Actions)
增长属性 (Growth Type)
战略归因与底层逻辑 (Strategic Attribution)1. 数字化样机时代
(1981 - 1998)"3D Design"
(3D 设计)CATIA
的独立与迭代Organic (核心)逻辑:物理替代
。最早的目标很简单:用 3D 数字模型完全替代 2D 图纸和物理黏土模型(Mockup)。这是达索的技术原点。
收购 SolidWorks
($3.1亿)
Inorganic (防御)逻辑:降维防御
。面对 Windows PC 带来的低端颠覆,达索没有选择忽视,而是直接买下最大的颠覆者,构建了高端 (CATIA) 与中端 (SW) 的双重护城河。2. PLM 时代
(1999 - 2011)"Product Lifecycle Management"
(全生命周期管理)提出 "PLM" 概念Concept (定义)逻辑:定义赛道
。Bernard Charlès 发明了 "PLM" 这个词。通过定义这个概念,达索强行将竞争维度从“画图工具”提升到了“流程管理”,迫使对手(如 PTC, Siemens)跟随它的游戏规则。
收购 MatrixOne
($4.08亿)
Inorganic (基石)逻辑:数据霸权
。为了实现 PLM,达索必须掌控数据流。收购 MatrixOne 提供了基于 Web 的无文件数据库技术,为后来的平台化奠定了技术地基。3. 体验经济时代
(2012 - 2018)"3DEXPERIENCE Platform"
(3D体验平台)推出 V6 架构 / 平台化Organic (颠覆)逻辑:消灭文件 (Zero File)
。这是达索最激进的战略。它试图消灭 CAD 行业通用的“文件格式”壁垒,强制所有数据都在数据库(平台)中流转。这制造了极高的客户迁移成本和粘性。
收购 Accelrys, Quintiq, Exa
Inorganic逻辑:全流程拼图
。为了让平台不仅仅是个空壳,必须填入科学(Accelrys)、规划(Quintiq)和仿真(Exa)能力,证明平台能处理非几何数据。4. 生命与万物孪生时代
(2019 - 2025)"Virtual Twin of Humans"
(人体虚拟孪生)收购 Medidata
($58亿)Inorganic (豪赌)逻辑:第二增长曲线
。当波音和空客的数字化已接近饱和,达索必须寻找一个新的复杂系统。人体(Biology)被视为比飞机更复杂的“机器”。收购 Medidata 是为了获得这一领域的入场券(临床数据)。
Generative Experience
(AI)
Organic (进化)逻辑:数据变现
。利用 3DEXPERIENCE 积累的 40 年工业数据和 Medidata 的临床数据,训练垂直领域的 AI 模型,从“辅助设计”进化为“生成设计”。深度战略解码 (Strategic Decoding)1. "概念发明家":夺取定义的权力 (The Power of Definition)
达索系统最可怕的能力不是写代码,而是造词。
• 现象:它先后发明或重新定义了 DMU (Digital Mockup), PLM (Product Lifecycle Management), 3DEXPERIENCE, Virtual Twin (注意它不用 Industry 4.0 这种通用词,而是坚持用自己的词)。
• 战略归因:通过发明新词汇,达索系统成功地掌握了话语权。当波音或特斯拉的高管接受了“体验 (Experience)”或“孪生 (Twin)”这些概念时,他们实际上就接受了达索的价值观和产品逻辑。这是一种最高级的营销战略。2. "消灭文件":技术护城河的极致 (The Zero File Doctrine)
• 背景:传统的 CAD/CAE 流程是基于文件的(.prt, .asm, .step)。文件容易丢失、版本混乱、且难以协同。
• 战略归因:达索系统花费 10 年时间(2006-2016),强行将底层架构从**“基于文件”切换为“基于数据库对象”**(即 3DEXPERIENCE 平台)。
• 结果:
• 短期痛苦:很多老用户(如奔驰)因为迁移太难而反抗,甚至一度威胁要换软件。
• 长期垄断:一旦迁移成功,竞争对手(如 Siemens, Ansys)几乎不可能把数据“挖”走,因为没有文件可以导出。所有的数据都只是数据库里的一个个对象链接。这构成了达索最坚固的技术壁垒。3. "家族企业的长视主义" (The Long-Termism)
• 背景:达索家族持有 ~40% 的股份和 >50% 的投票权。
• 战略归因:这使得管理层敢于做**“10年期”的赌注**。
• 2006年买 MatrixOne,直到 2014年 V6 平台才成熟(忍受 8 年阵痛)。
• 2019年买 Medidata,当时华尔街大骂“看不懂、太贵”,但达索不在乎股价波动,它看的是 2030 年的生命科学市场。
• 对比:Ansys 和 Synopsys 是典型的美式公众公司,必须照顾季度财报,因此它们的收购往往更务实、更即时见效;而达索的收购往往具有极其超前的战略意图。4. "从波音到心脏":通用方法的平移 (Universal Methodology)
• 逻辑:达索的核心哲学是**“系统工程 (Systems Engineering)”**。
• 战略归因:达索认为,造一架飞机和治愈一颗心脏,在底层逻辑上是一样的。都需要建模、仿真、验证、闭环。
• 飞机有 BOM (物料清单),人体有 Genome (基因组)。
• 飞机有风洞实验,人体有临床试验。
• Medidata 的价值:达索收购 Medidata,本质上是想把在航空航天领域验证了 40 年的“系统工程方法论”,平移到生命科学领域。这不只是一次跨界,这是一次方法论的殖民。总结
达索系统的战略归因可以概括为:“一个拥有家族耐心的哲学家,用数据库技术消灭了文件,用话语权定义了行业,现在正试图用造飞机的逻辑去解码生命。”
至此,我们已经完成了对 Ansys、Synopsys 和 Dassault Systèmes 三大巨头的全维度(产品、技术、资本、战略、创始人)深度复盘。这三家公司分别代表了物理仿真、电子设计和系统工程的最高峰。结语 (Epilogue)
最后的协调者:在物质、生命与自然之间
当我们合上达索系统的研究案卷,我们看到的不仅仅是一个商业帝国的版图,更是一种试图“数字化一切”的野心。
与其他竞争对手相比,达索系统最显著的特征在于它的“长视主义(Long-termism)”。在达索家族的掌控下,这家公司敢于做那些华尔街看不懂、但十年后会被证明是真理的事情——比如花费十年时间强行消灭 CAD 文件,比如花费 58 亿美元豪赌临床数据。
2025 年的达索系统,已经站在了一个新的十字路口:它成功地将造飞机的逻辑(系统工程)平移到了造汽车(特斯拉),现在正试图将其平移到造人(生命科学)。
• 在它的平台上,波音公司的工程师正在设计下一代碳中和飞机;
• 在它的平台上,医生正在名为“Living Heart”的虚拟心脏上模拟手术方案;
• 在它的平台上,城市规划者正在推演新加坡的数字孪生城市。
通过“虚拟孪生(Virtual Twin)”,达索系统打破了虚拟与现实的屏障。它告诉我们,工业不再是自然的对立面,只要通过精确的模拟与优化,产品、自然与生命可以达成一种动态的和谐。
至此,我们的三大巨头研究(Ansys, Synopsys, Dassault Systèmes)全部完成。
• Ansys 让我们看见了物理的深度;
• Synopsys 让我们看见了算力的密度;
• Dassault Systèmes 让我们看见了系统的广度。
这三家公司共同构成了现代人类文明的数字底座。只要人类还在通过制造工具来改造世界,它们的故事就永远不会结束。
模拟世界:Ansys 五十五年商业帝国兴衰与产品全景考 (1970-2025)
模拟世界:Ansys 五十五年商业帝国兴衰与产品全景考 (1970-2025)
工业软件本体级分类研究综述(EDA/CAD/CAE)- 前言 10万字级综述
工业软件本体级分类研究综述(EDA/CAD/CAE)- 第一部分
工业软件本体级分类研究综述(EDA/CAD/CAE)- 第二部分
2025工业软件全景研究 -(基于七大的研究,含详细表格)
并购
100 项与 Brown University 相关的药物交易
登录后查看更多信息
100 项与 Brown University 相关的转化医学
登录后查看更多信息
组织架构
使用我们的机构树数据加速您的研究。
登录
或

管线布局
2026年01月12日管线快照
管线布局中药物为当前组织机构及其子机构作为药物机构进行统计,早期临床1期并入临床1期,临床1/2期并入临床2期,临床2/3期并入临床3期
临床前
16
1
临床1期
其他
8
登录后查看更多信息
当前项目
| 药物(靶点) | 适应症 | 全球最高研发状态 |
|---|---|---|
Elraglusib ( GSK-3β ) | 结直肠癌 更多 | 临床1期 |
ONC-206 ( CLPP x D2 receptor x D3 receptor x ERK ) | 胆道癌 更多 | 临床前 |
ONC-212 ( CLPP x D2 receptor x D3 receptor x ERK x GPR132 ) | 放射性食管炎 更多 | 临床前 |
CB001(Brown University) ( CFLAR ) | 黑色素瘤 更多 | 临床前 |
MO-I-1182 ( HAAH ) | 乳腺癌 更多 | 临床前 |
登录后查看更多信息
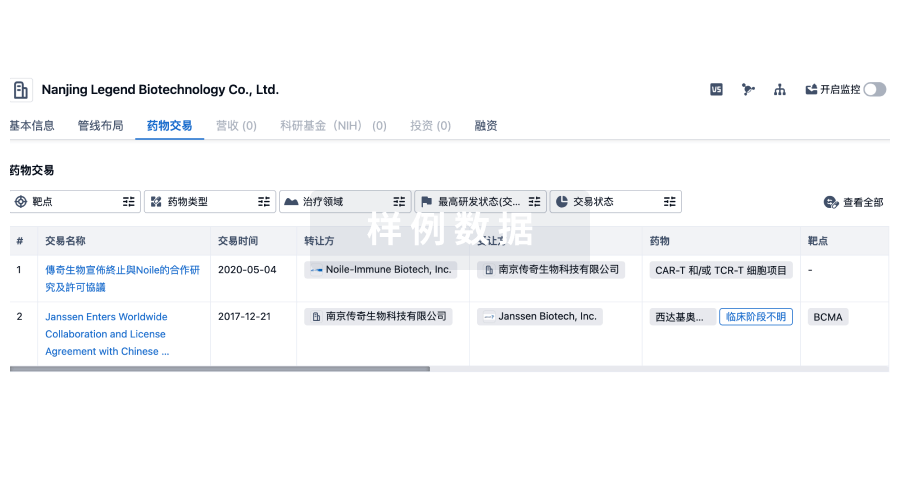
药物交易
使用我们的药物交易数据加速您的研究。
登录
或
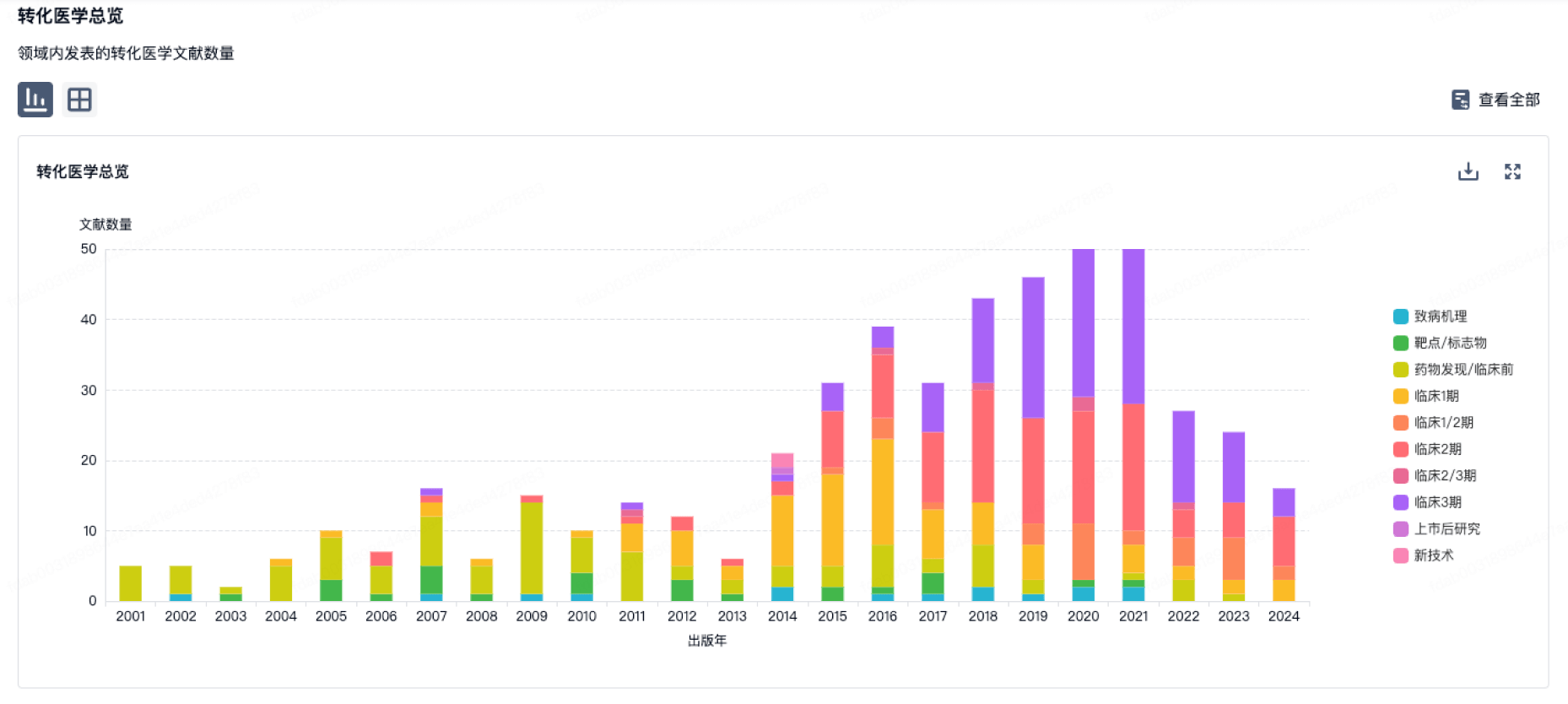
转化医学
使用我们的转化医学数据加速您的研究。
登录
或
营收
使用 Synapse 探索超过 36 万个组织的财务状况。
登录
或
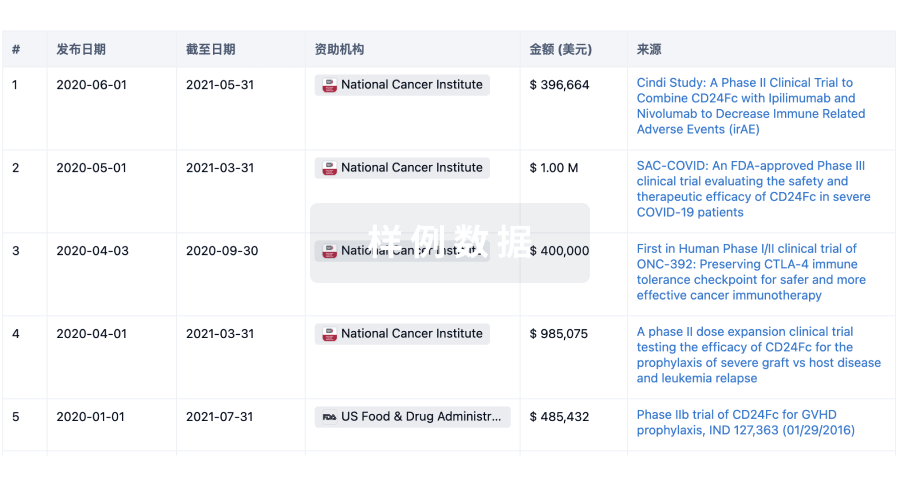
科研基金(NIH)
访问超过 200 万项资助和基金信息,以提升您的研究之旅。
登录
或
投资
深入了解从初创企业到成熟企业的最新公司投资动态。
登录
或
融资
发掘融资趋势以验证和推进您的投资机会。
登录
或
生物医药百科问答
全新生物医药AI Agent 覆盖科研全链路,让突破性发现快人一步
立即开始免费试用!
智慧芽新药情报库是智慧芽专为生命科学人士构建的基于AI的创新药情报平台,助您全方位提升您的研发与决策效率。
立即开始数据试用!
智慧芽新药库数据也通过智慧芽数据服务平台,以API或者数据包形式对外开放,助您更加充分利用智慧芽新药情报信息。
生物序列数据库
生物药研发创新
免费使用
化学结构数据库
小分子化药研发创新
免费使用





