预约演示
更新于:2026-01-10

InSilico Medicine Hong Kong Ltd.
更新于:2026-01-10
概览
标签
肿瘤
其他疾病
内分泌与代谢疾病
小分子化药
化学药
ADC
疾病领域得分
一眼洞穿机构专注的疾病领域
暂无数据
技术平台
公司药物应用最多的技术
暂无数据
靶点
公司最常开发的靶点
暂无数据
| 排名前五的药物类型 | 数量 |
|---|---|
| 小分子化药 | 49 |
| 化学药 | 10 |
| 未知 | 2 |
| ADC | 1 |
| 分子胶 | 1 |
关联
63
项与 英矽智能(香港)有限公司 相关的药物靶点 |
作用机制 ENaC阻滞剂 |
原研机构 |
非在研适应症- |
最高研发阶段批准上市 |
首次获批国家/地区 日本 |
首次获批日期1962-12-19 |
靶点 |
作用机制 ERs激动剂 [+1] |
非在研适应症- |
最高研发阶段临床3期 |
首次获批国家/地区- |
首次获批日期- |
作用机制 EGLN2抑制剂 [+1] |
在研机构 |
原研机构 |
非在研适应症- |
最高研发阶段临床2期 |
首次获批国家/地区- |
首次获批日期- |
10
项与 英矽智能(香港)有限公司 相关的临床试验NCT06724042
First-in-human Phase 1a/b, Open-Label, Multicenter, Dose Escalation, Optimization and Expansion Study of ISM5939 in Patients With Advanced and/or Metastatic Solid Tumors
This is a first-in-human Phase 1a/b, open-label, multicenter, dose escalation, optimization and expansion study of ISM5939 to evaluate the safety, tolerability, PK, PD, and preliminary antitumor activity of ISM5939 in patients with advanced or metastatic solid tumors.
The study will be conducted in 3 parts sequentially: Part 1 dose escalation ISM5939 monotherapy, Part 2 dose optimization to determine RP2D of ISM5939 monotherapy, and Part 3 dose expansion in 3 cohorts after initial safety run-in of ISM5939 combination therapy.
The study will be conducted in 3 parts sequentially: Part 1 dose escalation ISM5939 monotherapy, Part 2 dose optimization to determine RP2D of ISM5939 monotherapy, and Part 3 dose expansion in 3 cohorts after initial safety run-in of ISM5939 combination therapy.
开始日期2026-06-30 |
申办/合作机构 |
NCT07265570
A Phase IIa, Multicenter, Randomized, Double-blind, Placebo-controlled, Clinical Study to Evaluate the Safety, Tolerability, Pharmacokinetics and Clinical Efficacy of ISM5411 in Adult Patients With Active Ulcerative Colitis
This is a multicenter, randomized, double-blind, placebo-controlled study to evaluate the safety, tolerability, pharmacokinetics and clinical efficacy of ISM5411 in adult patients with active ulcerative colitis.
开始日期2025-12-10 |
申办/合作机构 |
NCT06414460
A Phase 1, Open-Label, Multicenter, First-in-Human Study to Evaluate the Safety, Tolerability, Pharmacokinetics/Pharmacodynamics, and Preliminary Efficacy of ISM3412 in Participants With Locally Advanced/Metastatic Solid Tumors
The study has consists of two parts, a dose escalation part (Part 1) and a dose selection optimization part (Part 2). The primary objectives of this study are to evaluate the safety and tolerability of ISM3412 in participants with locally advanced/metastatic solid tumors, and to determine the RP2D of ISM3412.
开始日期2025-04-25 |
申办/合作机构 |
100 项与 英矽智能(香港)有限公司 相关的临床结果
登录后查看更多信息
0 项与 英矽智能(香港)有限公司 相关的专利(医药)
登录后查看更多信息
73
项与 英矽智能(香港)有限公司 相关的文献(医药)2025-12-17·Future Medicinal Chemistry
Recent advance in macrocyclic CDK inhibitors
Review
作者: Ren, Feng ; Ding, Xiao ; Zhang, Zhisen ; Zhavoronkov, Alex ; Shi, Ryan ; Zheng, Jiamin ; Liu, Jinxin
Cyclin-dependent kinases (CDKs) are central regulators of the cell cycle progression and transcription, making them attractive targets especially in oncology. The clinical success of CDK4/6 inhibitors in hormone receptor-positive (HR+) and HER2-negative (HER2-) breast cancer has highlighted the therapeutic potential of CDK inhibition, along with ongoing clinical evaluation of other CDK-targeted agents. Despite the progress, challenges still remain due to off-target toxicity and the emergence of resistance. Recently, macrocycle-based drug design has gained recognition for its ability to enhance the kinase inhibitory activities and selectivity, improve drug-like properties, and potentially overcome resistance. This review summarizes recent advances (2015-2025) in macrocyclization strategies for CDK inhibitors, tracing the structural modification process from the acyclic scaffolds and highlighting their potential to address key limitations of current therapies.
2025-12-01·AGEING RESEARCH REVIEWS
From clock to clock: Therapeutic target discovery for aging and age-related diseases
Review
作者: Gennert, David ; Leung, Geoffrey Ho Duen ; Chen, Jianjiu ; Ren, Feng ; Shneyderman, Anastasia ; Aliper, Alex ; Ustiugova, Alina ; Korzinkin, Mike ; Leung, Howell ; Zhavoronkov, Alex ; Pun, Frank W
The aging population worldwide necessitates the development of novel therapeutics that enhance the quality of life by preventing and treating age-related diseases. In this review, we first discuss the advantages of a dual-purpose target identification strategy for aging and age-related diseases, with assessment of the hallmarks of aging as an approach to identify such dual-purpose targets. Resulting from a convergence of aging research with machine learning (ML) and other artificial intelligence (AI) models, aging clocks were initially developed as aging biomarkers, but its value in identifying therapeutic targets is also increasingly recognized. Building on recently published aging clocks, we reestablish a significant proportion of known drug targets by identifying clock-associated genes, highlighting the potential of these clocks for target identification. Lastly, we discuss other applications of aging clocks in drug development such as population stratification and disease and treatment monitoring. With the growing availability of multi-omics data and rapid advancements in ML and AI, we anticipate accelerated progress in aging clock research, paving the way for innovative treatments to meet the healthcare needs of a global aging population.
2025-10-01·JOURNAL OF BIOLOGICAL CHEMISTRY
Pyrimethamine and a potent analog inhibit NRF2 by suppressing one-carbon metabolism
Article
作者: Bowman, Brittany M ; Chen, Xiaoxin ; Wang, Haining ; Wilkerson, Emily ; Major, Michael B ; Lapak, Kyle ; Cho, Kevin ; Medcalf, Matthew R ; Zolkind, Paul ; Patti, Gary J ; Dolle, Roland E ; Wamsley, Nathan T ; Paiboonrungruang, Chorlada ; Chembo, Julius
Nuclear factor erythroid 2-related factor 2 (NFE2L2/NRF2) is a critical mediator of the cellular oxidative stress response. Aberrant activation of NRF2 is common in lung and upper aerodigestive cancers, where it promotes tumor initiation and progression and confers resistance to chemotherapy, radiation therapy, and immune checkpoint inhibitors. As such, NRF2 therapeutic inhibitors are actively being sought. We previously reported that the antiparasitic drug pyrimethamine (PYR) inhibits NRF2 in cell lines and in a NRF2-inducible genetically engineered mouse model. Here we design, synthesize, and define structure-activity relationships across a series of 25 PYR-based derivatives to reveal WCDD115 as a 22-fold more potent inhibitor of NRF2 (57 nM versus 1.2 μM). PYR is known to inhibit plasmodial and human dihydrofolate reductase (DHFR). We found that WCDD115 inhibits hDHFR with 31-fold greater potency than PYR (144 nM versus 4.49 μM). Metabolomics showed strong similarities between PYR, WCDD115 and methotrexate. Genetic, pharmacological and metabolic epistasis studies reveal that DHFR inactivation is required for NRF2 suppression by WCDD115 and PYR. Global and targeted proteomics revealed overlapping profiles for WCDD115, PYR and methotrexate, including suppression of NRF2 oxidative stress response and activation of TP53 and the DNA damage response. Therefore, PYR and a novel potent derivative WCDD115 are effective, indirect inhibitors of NRF2 and its antioxidant functions. These data underscore the importance of one-carbon metabolism for the NRF2 signaling pathway and support a new therapeutic strategy to suppress NRF2-driven cancer biology.
2,557
项与 英矽智能(香港)有限公司 相关的新闻(医药)2026-01-09
·雪球
事件:2026年CES展黄仁勋演讲覆盖AI4S(AIforScience),而2024年英伟达GTC已将其列为AI三大关键方向,AI4S(人工智能驱动科学研究)赛道热度快速提升------------------------志特新材主营业务:专注于新型节能环保材料研发、生产与销售,核心产品包括铝模板系统、相变微胶囊材料、MOFs材料等,广泛应用于建筑、新能源、冷链物流等领域,是国内领先的绿色建材供应商。AI4S关联性:A股首家明确布局AI4S的企业,与量子科技长三角产业创新中心、微观纪元等共建“量子+AI”新材料研发体系;成立控股子公司志特小临智能科技,专注化学机器人平台及AI4S新材料研发,已签订420份AI4S业务合同,进入工信部重点推广名录。道氏技术主营业务:国内领先的新能源材料综合服务商,核心产品包括锂电正极材料、碳纳米管导电剂、陶瓷材料等,覆盖新能源电池全产业链,同时布局氢能、固态电池等前沿领域广东道氏技术股份有限公司。AI4S关联性:通过“芯片-算法-算力-材料”全链条布局AI4S,合资成立赫曦原子智算中心(持股80%),2025年8月落地全球首座规模化原子级科学计算智算中心;参股芯培森研发APU芯片,相较传统CPU/GPU架构算力提升1-2个数量级,能耗降低2-3个数量级,加速固态电解质等材料研发从“经验试错”到“数据智能”转型。美迪西主营业务:国内领先的临床前医药研发服务企业(CRO),提供从药物发现到临床前研究的一站式服务,涵盖药物合成、药效学、药代动力学、毒理学等核心环节,服务全球数百家制药企业。AI4S关联性:GTC认证的“AI制药国家队”,搭建AI药物发现平台,提供蛋白结构预测与模拟、靶点结合位点解析等技术服务;与英矽智能、德睿智药等AI创新药公司深度合作,通过“AI生成分子+实验验证”模式加速肿瘤管线研发,显著提高药物研发效率美迪西。博彦科技主营业务:全球领先的IT咨询、解决方案与服务提供商,业务涵盖企业应用开发与维护、大数据分析、人工智能服务等,为金融、医疗、高科技等行业客户提供数字化转型服务。AI4S关联性:AI4S领域“铲子股”,开发化合物逆合成路线设计系统(准确率72.2%)、反应条件试剂推荐系统(准确率98.7%);打造以大模型为中枢的全自动智能化学实验室,可自主规划实验流程并联动机械臂完成分子合成,大幅提升科研生产力。东阳光主营业务:综合性制药企业,核心产品包括抗流感药物、糖尿病药物等,同时布局创新药、生物药、ADC药物等前沿领域,构建覆盖小分子、小核酸、CAR-T等多类型药物的自主研发体系。AI4S关联性:2025年8月推出全球首个药物制剂垂直领域自然语言大模型HEC-PharmAI,填补该领域AI大模型应用空白;联合华为云、深势科技打造“AI+生物医药”生态体系,构建从靶点发现到临床研究的药物研发全流程AI赋能体系,加速代谢疾病等管线研发。泰坦科技主营业务:国内领先的科学服务提供商,产品涵盖科研试剂、实验仪器、实验室建设等,为高校、科研院所、企业研发中心提供一站式科研服务解决方案。AI4S关联性:科创板AI4S科研服务龙头,打造高通量材料AI智能合成平台,提供材料研发全流程智能化解决方案;通过AI算法优化实验设计与数据分析,帮助客户降低研发成本30%以上,缩短研发周期50%,服务覆盖新材料、生物医药等多个领域。软通动力主营业务:全栈式数字服务提供商,提供软件开发、云计算、大数据、人工智能等技术服务,服务于金融、电信、制造等行业,研发天璇MaaS大模型服务平台,为企业提供一站式大模型解决方案。AI4S关联性:在2025世界人工智能大会上提出AIForScience作为新质生产力源头创新的战略定位;构建AI4S全栈产品体系,在钢铁、教育等行业落地AI模型应用,如钢铁行业生产能耗降低15%,教育领域学习效果提升20%,同时为科研机构提供AI大模型定制化服务。每日互动主营业务:国内领先的数据智能服务商,基于大数据技术提供增长服务、品牌服务、公共服务等,核心产品包括个推SDK、个知AI系列产品,服务于互联网、金融、政务等多个领域。AI4S关联性:与DeepSeek深度合作,提供脱敏行业数据用于AI4S模型训练,同时利用DeepSeek技术优化自身数据智能平台;在AI4SE(AIforScienceandEngineering)领域布局,通过AI算法提升科研数据处理效率,为生物医药、材料科学等领域提供数据智能解决方案。.中科曙光主营业务:国内高性能计算龙头企业,核心产品包括曙光系列服务器、存储设备、云计算平台等,同时提供算力服务、大数据解决方案,是国内AI基础设施建设的核心供应商。AI4S关联性:为AI4S领域提供核心算力支撑,曙光AI服务器广泛应用于材料模拟、药物研发、基因测序等科研场景;与中科院等科研机构合作,开发AI4S专用算力平台,优化科学计算算法,大幅提升AI4S应用的计算效率,降低科研成本。英矽智能(03696.HK):港股“AI制药第一股”,端到端AI平台将药物研发周期压缩6倍,10个分子获临床试验许可,引入礼来、腾讯等基石投资者。药明康德(603259.SH):CXO龙头+AI全链条赋能,化合物筛选效率提升40倍,AI相关订单占比达35%,服务全球18家顶级药企。泓博医药(301230.SZ):自研PR-GPT大模型优化药物设计,效率提升50%,IND申报成功率行业前三,获默沙东、辉瑞等跨国药企合作订单。阿尔特(300825.SZ):汽车研发AI4S龙头,AI工具使仿真测试效率提升10倍,与英伟达合作搭建算力底座,服务特斯拉、比亚迪等客户。
核酸药物
2026-01-09
引言:从实验室到生活场景的跨越
2023年ChatGPT的全球爆红标志着AI大模型技术正式进入大众视野。这类拥有千亿级参数的智能系统,正以惊人的速度渗透到医疗、教育、金融等各个领域。据斯坦福大学《2024年AI指数报告》显示,全球AI大模型数量已突破300个,其中中国贡献了40%的增量。这种技术革命不仅改变了人机交互方式,更正在重构整个社会的运行逻辑。技术原理:神经网络中的"大脑"进化
AI大模型的核心是深度神经网络,通过海量数据训练实现"涌现能力"。以GPT-4为例,其1750亿参数构成的模型在自然语言处理上展现出类人的推理能力。这种能力源于三个关键突破:
Transformer架构:2017年Google提出的注意力机制,使模型能同时处理文本中的远距离依赖关系
预训练-微调范式:先在通用数据上预训练,再针对特定任务微调,大幅提升迁移学习效率
规模定律:模型性能与参数规模、数据量、计算量呈幂律关系,推动参数规模从亿级向万亿级跃进应用场景:从效率提升到范式革命医疗领域:从辅助诊断到新药研发
诊断辅助:北京协和医院部署的"大模型+医生"系统,将罕见病诊断时间从平均7天缩短至2小时
药物发现:英矽智能的Pharma.AI平台通过生成式AI设计全新靶点,将新药研发周期从5年压缩至18个月
健康管理:个性化健康助手能根据用户生活习惯生成预防性医疗方案教育变革:从标准化教学到因材施教
智能导师:可汗学院AI助手能实时分析学生解题步骤,提供针对性指导
内容生成:教师用AI快速生成教案、习题和评估报告,备课效率提升60%
语言学习:多模态AI可模拟真实对话场景,实现沉浸式语言训练金融创新:从风险控制到智能投顾
信贷评估:蚂蚁集团的风控系统通过分析2000+维度的数据,将不良贷款率控制在0.8%
量化交易:摩根大通的LOXM系统利用AI预测市场走势,交易执行速度达微秒级
财富管理:智能投顾平台根据用户风险偏好动态调整资产配置,管理规模已突破5000亿美元工业制造:从流程优化到智能决策
预测性维护:西门子MindSphere平台通过设备传感器数据预测故障,减少停机时间30%
工艺优化:台积电利用AI调整芯片制造参数,良品率提升至99.9%
供应链管理:京东物流的智能调度系统使配送效率提升40%挑战与对策:在创新与规范间寻找平衡技术层面
数据偏见:通过对抗性训练和公平性约束算法缓解
能耗问题:采用稀疏化训练、模型蒸馏等技术降低计算成本
可解释性:开发SHAP值、LIME等解释工具增强模型透明度伦理层面
制定AI伦理准则:欧盟《AI法案》要求高风险AI系统必须通过合规评估
建立问责机制:明确AI决策失误时的责任主体
保护数据隐私:采用联邦学习、同态加密等技术实现数据可用不可见产业层面
培养复合型人才:清华大学等高校开设"AI+X"交叉学科专业
构建开源生态:Meta的LLaMA系列开源模型降低技术门槛
发展专用芯片:华为昇腾、寒武纪等AI芯片提升算力效率未来展望:人机协同的新纪元
2024年Gartner预测,到2026年80%的企业将使用AI大模型。未来的发展方向包括:
多模态融合:文本、图像、视频、传感器的统一处理
具身智能:AI与机器人结合实现物理世界交互
自主进化:模型能自我更新知识库和算法
社会适配:AI系统理解并适应不同文化背景结语:在技术浪潮中把握方向
AI大模型正在引发第四次工业革命,其影响将超越蒸汽机、电力、计算机带来的变革。面对这个充满机遇与挑战的新时代,我们需要在技术创新与伦理规范之间找到平衡点,让AI真正成为推动人类文明进步的积极力量。正如图灵奖得主Yann LeCun所言:"AI的未来不是取代人类,而是扩展人类的能力边界。"
生物类似药
2026-01-09
·搜狐新闻
01广信材料:子项目PCB光刻胶1.6万吨及自制树脂1.2万吨已经实现正式生产每日经济新闻7日消息,1月7日,广信材料在互动平台表示,公司龙南基地正按照既定计划有序推进中,截至目前,公司已完成大部分厂房建设和设备产线布局,并有多个子项目已经开始生产,其中子项目PCB光刻胶1.6万吨及自制树脂1.2万吨已经实现正式生产,其他子项目预计于2026年上半年提交试生产申请。02XREAL:谷歌重金押注中国AR企业与XREAL深化战略合作36氪7日消息,CES 2026期间,谷歌与XREAL联合宣布达成深度长期战略合作。来自中国的AR创新企业XREAL是谷歌在AR眼镜领域的唯一硬件合作伙伴,已连续四年独占全球AR眼镜市场份额第一,双方首款合作产品Project Aura将于今年上市。03箭元科技:国内首个海上回收复用火箭基地落户杭州 “钱塘号”火箭预计年底首飞财闻8日消息,据钱塘发布消息,近日,箭元科技中大型液体运载火箭总装总测及回收复用基地在钱塘破土动工。标志着国内首个海上回收复用火箭产能基地,也是首个不锈钢火箭超级工厂正式启航。与此同时,以钱塘命名的“钱塘号”火箭同步亮相。据悉,箭元科技中大型液体运载火箭生产试验及总装总测基地包括回收复用中心、检测检验中心、生产制造中心,项目总投资52亿元,建成后将具备年产25发火箭的规模化制造能力。根据计划,今年8月底,作为箭元科技自主研发的国内首个“液氧甲烷+不锈钢+海上回收”火箭,“元行者一号”将在这里开始总装测试,年底首枚“钱塘号”火箭将执行首次飞行及回收任务。04崇德科技:核心零部件批量供应国际龙头抢占算力能源赛道人民财讯8日电,近日,崇德科技宣布,行星齿轮箱销轴、联轴器轴承等核心产品正式向国际头部齿轮箱企业批量交付。该批产品将精准配套17.5MW燃气轮机,而这款燃气轮机正是全球能源装备龙头企业为AI算力场景量身打造的关键发电设备,未来一年将完成50余台套产品交付,标志着崇德科技进一步深度切入AI算力能源供给核心链条。05英矽智能:与施维雅达成8.88亿美元抗肿瘤药物研发合作格隆汇6日消息,1月5日,英矽智能宣布与施维雅(Servier)达成一项总金额达8.88亿美元的抗肿瘤药物研发合作。根据协议,英矽智能将有资格获得最高3200万美元的首付款及近期研发里程碑付款,并将主导利用其人工智能技术平台,发现并开发符合既定标准的潜在候选药物;施维雅将共同承担研发成本,并主导后续临床验证及商业化进程。06GGII:预计2026年国内人形机器人产量将达到6.25万台中证报7日消息,继2025年奠定“量产元年”基础后,2026年人形机器人产业将正式迈入规模化放量的关键阶段。高工机器人产业研究所数据显示,2025年国内人形机器人出货量预计达1.8万台,较2024年激增超650%;在此基础上,2026年国内出货量有望攀升至6.25万台。浙江人形机器人创新中心首席科学家熊蓉接受采访时更明确指出,“预计2026年我国人形机器人产量将达到10万至20万台级。”07乘联分会:2025年12月全国乘用车新能源车市场零售138.7万辆同比增长7%IT之家7日消息,乘联分会数据显示,2025年12月1-31日,全国乘用车市场零售229.6万辆,2025年以来累计零售2377.9万辆。新能源车方面,12月全国乘用车新能源车市场零售138.7万辆,同比去年同期增长7%,较上月增长5%,2025年以来累计零售1285.9万辆,同比增长18%;2025年12月1-31日,全国乘用车厂商新能源批发155.4万辆,同比去年同期增长3%,较上月下降9%,2025年以来累计批发1531万辆,同比增长25%。来源:人民财讯、财闻、IT之家等编辑:陆映乔返回搜狐,查看更多
引进/卖出
100 项与 英矽智能(香港)有限公司 相关的药物交易
登录后查看更多信息
100 项与 英矽智能(香港)有限公司 相关的转化医学
登录后查看更多信息
组织架构
使用我们的机构树数据加速您的研究。
登录
或

管线布局
2026年01月15日管线快照
管线布局中药物为当前组织机构及其子机构作为药物机构进行统计,早期临床1期并入临床1期,临床1/2期并入临床2期,临床2/3期并入临床3期
药物发现
20
36
临床前
临床申请批准
1
4
临床1期
临床2期
2
8
其他
登录后查看更多信息
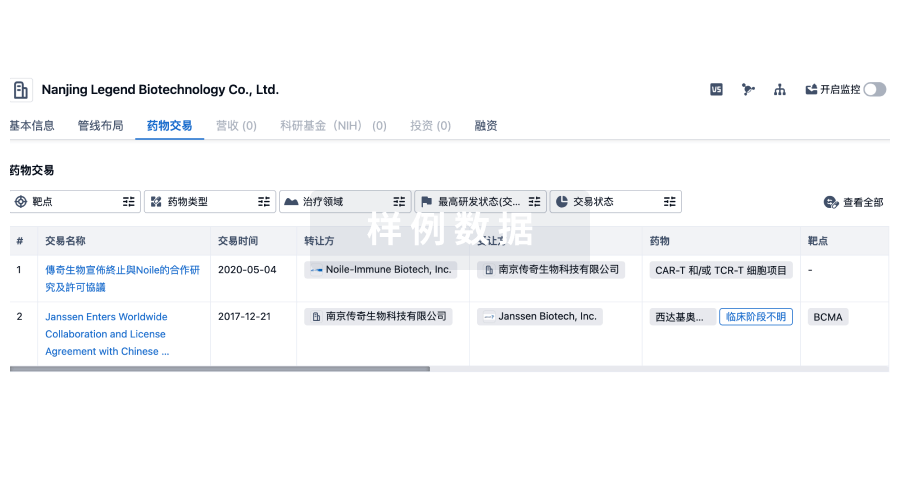
药物交易
使用我们的药物交易数据加速您的研究。
登录
或
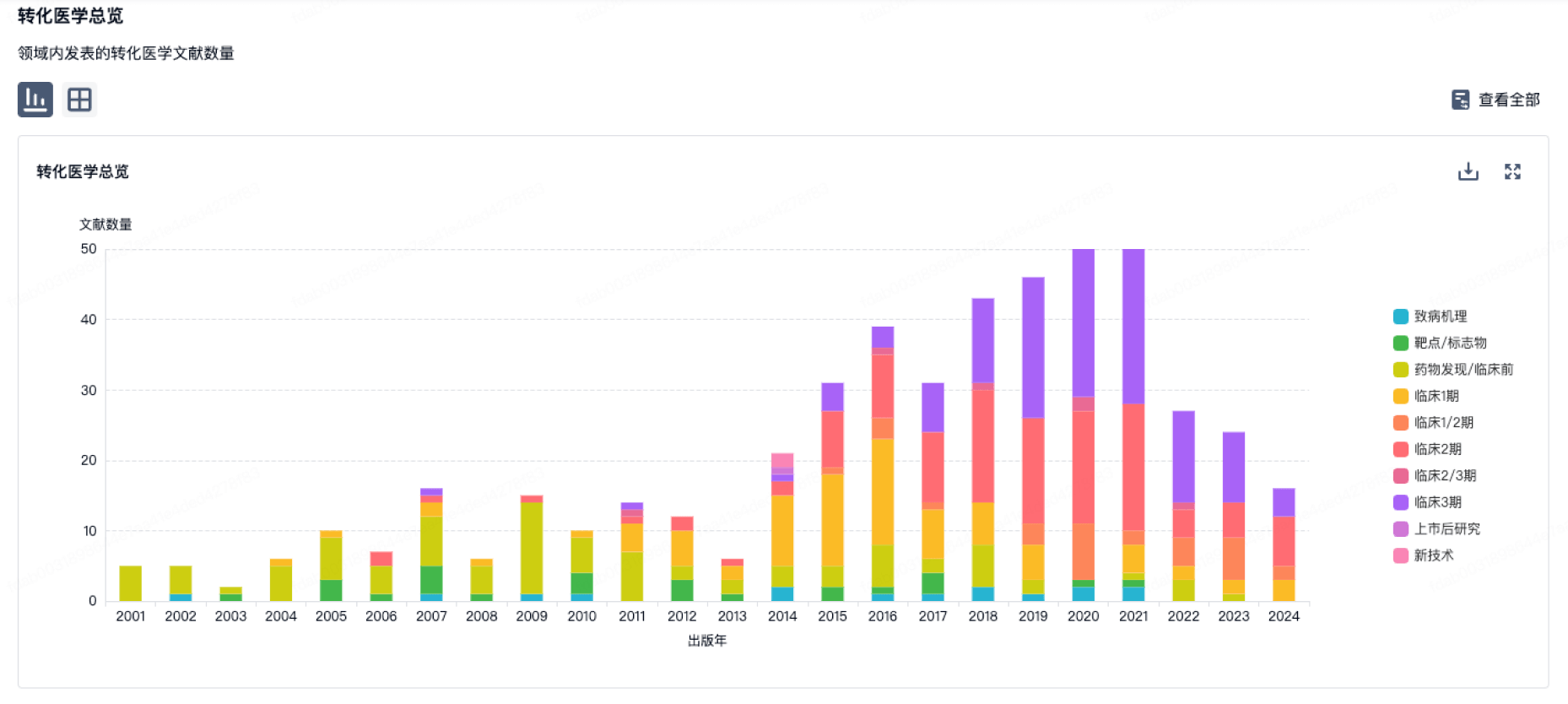
转化医学
使用我们的转化医学数据加速您的研究。
登录
或
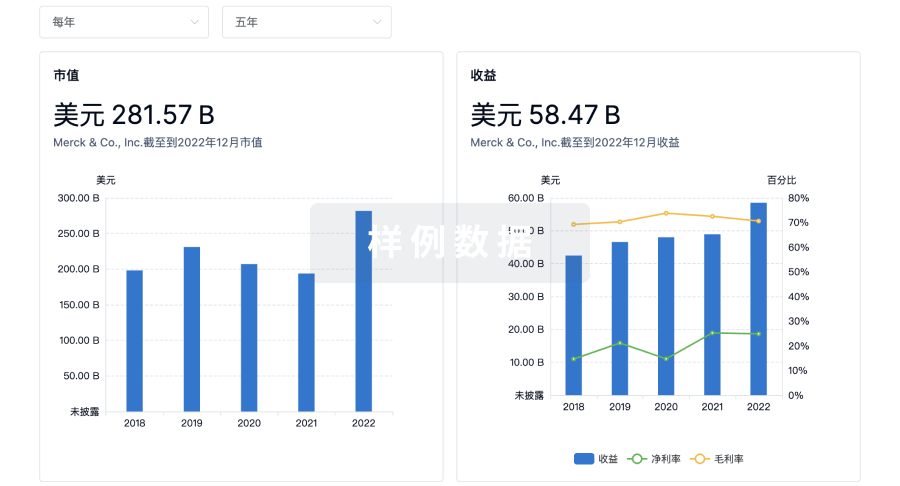
营收
使用 Synapse 探索超过 36 万个组织的财务状况。
登录
或
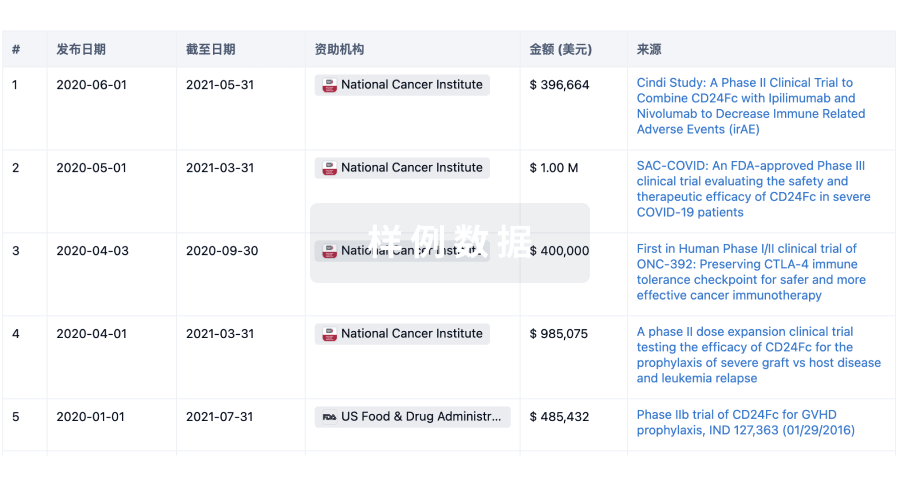
科研基金(NIH)
访问超过 200 万项资助和基金信息,以提升您的研究之旅。
登录
或
投资
深入了解从初创企业到成熟企业的最新公司投资动态。
登录
或
融资
发掘融资趋势以验证和推进您的投资机会。
登录
或
生物医药百科问答
全新生物医药AI Agent 覆盖科研全链路,让突破性发现快人一步
立即开始免费试用!
智慧芽新药情报库是智慧芽专为生命科学人士构建的基于AI的创新药情报平台,助您全方位提升您的研发与决策效率。
立即开始数据试用!
智慧芽新药库数据也通过智慧芽数据服务平台,以API或者数据包形式对外开放,助您更加充分利用智慧芽新药情报信息。
生物序列数据库
生物药研发创新
免费使用
化学结构数据库
小分子化药研发创新
免费使用


